Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-09T22:30:50.405Z Has data issue: false hasContentIssue false
  • English
  • Français

Reservoir Layers in High Tc Mercury Cuprates

Published online by Cambridge University Press:  10 February 2011

T. H. Geballe ,
Boris Y. Moyzhes  and
P. H. Dicktnson
T. H. Geballe
Affiliation:
Dept. of Applied Physics, Stanford University, Stanford, CA 94305, [email protected]
Boris Y. Moyzhes
Affiliation:
E. L. Ginzton Laboratory, Stanford University, Stanford, CA 94305
P. H. Dicktnson
Affiliation:
Chromatic Research Inc., Sunnyvale, CA 94089
Get access

Abstract

We put forward the hypothesis that cations with 6s electrons (Hg,Tl,Pb,Bi) in the charge reservoir layers of high Tc cuprate superconductors actively participate in the pairing interaction as negative-U centers. We further argue that the Hg-cuprates are outstanding superconductors (Tc > 160 K) because they can exist as two-ion negative-U centers, 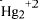. Their electrons are less localized than in single-site centers (negative-U or bipolaron) and can have a strong pairing interaction with a smaller increase in effective mass. The 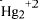centers are oriented in the x and y directions and can have phase differences compatible with the d-wave symmetry of the CuO2 planes.

Type
Research Article
Information
MRS Online Proceedings Library (OPL) , Volume 574: Symposia BB – Multicomponent Oxide Films for Electronics , 1999 , 151
Copyright
Copyright © Materials Research Society 1999

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

1. Anderson, P. W., Phys. Rev. Lett. 34, p. 953 (1975).10.1103/PhysRevLett.34.953Google Scholar
2. Copious REFERENCES, including Tc and pressure dependences of Tc for the cuprates are given, for example, by Takahashi, H. and Mori, N. in Studies Of High Temperature Superconductors, edited by Narlikar, A. V., (Nova Science 16, Commack, NY 1996), p. 1–55.Google Scholar
3. Cotton, F.A. and Wilkinson, G., Advanced Inorganic Chemistry (5th ed) ( John Wiley & Sons, New York, NY 1988)Google Scholar
4. Moyzhes, B. Y. and Drabkin, A., Sov. Phys. Sol. St. 25, p. 7 (1983).Google Scholar
5. s Chakraverty, B. K., Ranninger, J. D. and Feinberg, D., Phys. Rev. Lett. 81, p. 433 (1998)10.1103/PhysRevLett.81.433Google Scholar
6. Kaidanov, V. I. and Ravich, Yu. I., Sov. Phys. Usp. 28(1), p. 31 (1985).10.1070/PU1985v028n01ABEH003632Google Scholar
7. See for example Chu, C. W., Gao, L., Chen, F., Huang, Z. J., Meng, R. L., and Xu, Y. Y., Nature, 365 p. 323 (1993). More complete data are cited in ref 2.10.1038/365323a0Google Scholar
8. Singh, D. J. and Pickett, W. E., Phys. Rev. Lett. 73, p. 476 (1994).10.1103/PhysRevLett.73.476Google Scholar
9. Uemura, Y. J., Physica C 282, p. 194 (1997).10.1016/S0921-4534(97)00194-9Google Scholar
10. Armstrong, R. S., David, W. I. F., Loveday, J. S., Gameson, I., Edwards, P. P., Capponi, J. P., Bordet, P., and Marezio, M., Phys. Rev. B 52, p. 15551 (1995); A. M. Balagurov, D. V. Sheptyakov, V. L. Aksenov, E. V. Antipov, S. N. Putilin, P. G. Radaelli, and M. Marezio, Phys. Rev. B 59, p. 7209 (1999).10.1103/PhysRevB.52.15551Google Scholar
11. McWhan, D. B., Rice, T. M., and Remeika, J. P., Phys. Rev. Lett. 23, p. 1384 (1969).10.1103/PhysRevLett.23.1384Google Scholar
12. Chmaissen, O., Jorgenson, J. D., Yamaura, K., Hiroi, Z., Takano, M., Shimoyama, J., and Kishio, K., Phys. Rev. B 53, p. 14647 (1996).10.1103/PhysRevB.53.14647Google Scholar
13. Cherhik, I. A., Lykov, S. N., Pisma Zh. Eksp. Teor. Fiz. 7, p. 94 (1981); I. A. Cherhik, S. N. Lykov, Sov. Phys. Sol. St., 23, p. 817 (1981).Google Scholar