Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-09T06:12:59.514Z Has data issue: false hasContentIssue false
  • English
  • Français

Reaction Kinetics at a Fluctuating Surface: Proton Exchange in Proteins

Published online by Cambridge University Press:  15 February 2011

T. Gregory Dewey
T. Gregory Dewey*
Affiliation:
Department of Chemistry, University of Denver, Denver, CO 80208.
Get access

Abstract

Experimental data for the exchange of protons between proteins and the aqueous solvent is re-examined using a fractal model. The fraction of protons unexchanged from the protein, f is seen to follow a stretched exponential, 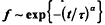at long times. For the protein, lysozyme, data over a range of temperatures were considered and accurate fits were obtained with a single, unadjusted scaling exponent, α. The time constant, τ, followed an Arrhenius law and gave an activation energy comparable to that obtained for free peptide exchange. A model is proposed where proton exchange occurs as a result of solvent reacting at the fractal surface of the protein. The protein itself is not treated as static but has units that diffuse to the surface. The diffusion of these units in the long time domain is assumed to be classical. In this model the scaling exponent, α, is related to the spectral dimension of the system. Treating the problem as a reaction of the type A+B→C in a confined region, the exponent is given by: α = (3 − ds)/4 where dS/4 is the fractal surface dimension of the protein. Using the value of 2.17 previously established for the surface dimension of lysozyme, data at 6 different temperatures could be fit with the corresponding α of 0.21. These results show that the fractal structure of a protein can influence difflusional processes of small molecules associating with the protein.

Type
Research Article
Information
MRS Online Proceedings Library (OPL) , Volume 366: Symposium N – Dynamics in Small Confining Systems , 1994 , 409
Copyright
Copyright © Materials Research Society 1995

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Welch, G.R., The Fluctuating Enzyme (John Wiley & Sons, New York, 1986).Google Scholar
2. Dewey, T.G., Proc. Natl. Acad. Sci. USA (in press,, 1994).Google Scholar
3. Wickett, R.R., Ide, G.J., and Rosenberg, A., Biochemistry 13, 3273 (1974).Google Scholar
4. Kopelman, R., Science 241, 1620 (1988).Google Scholar
5. Zumofen, G., Blumen, A., and Klafter, J., J. Chem. Phys. 82, 3198 (1985).Google Scholar
6. Kang, K., and Redner, S., Phys. Rev. Lett. 52, 955 (1984).Google Scholar
7. Havlin, S., in The Fractal Approach to Heterogeneous Chemistry, edited by Avnir, D., (Wiley, Chichester, 1989) Chap. 4.1.1.Google Scholar
8. Pfeifer, P., Welz, U., and Wippermann, H., Chem. Phys. Lett. 113, 535 (1985).Google Scholar
9. deGennes, P., J. Chem. Phys. 76, 3316 (1982).Google Scholar
10. Englander, S.W., and Poulsen, A., Biopolymers 7, 329 (1969).Google Scholar
11. Agmon, N., J. Chem. Phys. 81, 2811 (1984).Google Scholar
12. Szabo, A., J. Chem. Phys. 95, 2481 (1991).Google Scholar
13. Agmon, N., and Szabo, A., J. Chem. Phys. 92, 5270 (1990).Google Scholar
14. Lee, S., and Karplus, M., J. Chem. Phys. 86, 1883 (1987).Google Scholar
15. Eigen, M., Zeitschrift Phys. Chem. (Frankfurt) 12, 176 (1954).Google Scholar
16. Zwanzig, R., and Szabo, A., Biophys. J. 60, 671 (1991).Google Scholar
17. Gradshteyn, I.S., and Ryzhik, I.M., Tables of Integrals, Series and Products (Academic Press, New York, 1980) pp. 285.Google Scholar
18. Olver, F.W.J., Asymptotics and Special Functions (Academic Press, New York, 1974) pp. 190–195.Google Scholar