Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-27T02:04:22.614Z Has data issue: false hasContentIssue false
  • English
  • Français

Quantum-Well Contributions to the RKKY Coupling in Magnetic Multilayers

Published online by Cambridge University Press:  03 September 2012

B. A. Jones  and
C. B. Hanna
B. A. Jones
Affiliation:
IBM Research Division, Almaden Research Center, K31/802, 650 Harry Road, San Jose, CA 95120–6099
C. B. Hanna
Affiliation:
IBM Research Division, T. J. Watson Research Center, R.O. Box 218, Yorktown Heights, NY 10598
Get access

Abstract

We study the effects of quantum-well states on the calculated RKKY coupling. We find that the bound states of a finite-size potential well of depth V give an added oscillation period of size 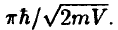For the simplest case of a spherical free-electron Fermi surface, thus two periods appear: the original, “fast,” π/kf oscillation, and the quantum-well one 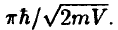The quantum-well contributions have larger amplitude, and are in fact the predominant oscillation. For physically reasonable V (tenths of an eV) this period is around 8–10Å. We discuss evidence for these effects in experimental systems.

Type
Research Article
Information
MRS Online Proceedings Library (OPL) , Volume 313: Symposium Q1 – Magnetic Ultrathin Films, Multilayers and Surfaces/Magnetic Interfaces-Physics and Characterizations , 1993 , 165
Copyright
Copyright © Materials Research Society 1993

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

1. Unguris, J., Celotta, R. J., and Pierce, D. T., Phys. Rev. Lett. 67, 140 (1991).Google Scholar
2. The following work covers study of several spacer Materials. Parkin, S. S. P., More, N., and Roche, K. P., Phys. Rev. Lett. 64, 2304 (1990);Google Scholar
Parkin, S. S. P., Bhadra, R., and Roche, K. P., Phys. Rev. Lett. 66, 2152 (1991);Google Scholar
Parkin, S. S. P., Phys. Rev. Lett. 67, 3598 (1991).Google Scholar
3. Bruno, P. and Chappert, C., Phys. Rev. Lett. 67, 1602 (1991);Google Scholar
Chappert, C. and Renard, J. P., Europhys. Lett. 15, 553 (1991).Google Scholar
4. Wang, Y., Levy, P. M., and Fry, J. L., Phys. Rev. Lett. 65, 2732 (1990);Google Scholar
Fry, J. L., Ethridge, E. C., Levy, P. M., and Wang, Y., J. Appl. Phys. 69, 4780 (1991).Google Scholar
5. Herman, F., Sticht, J., and Van Schilfgaarde, M., J. Appl. Phys. 69, 4783 (1991); F. Herman and R. Schrieffer, Phys. Rev. B, to be published.Google Scholar
6. Deaven, D. M., Rokhsar, D., and Johnson, M., Phys. Rev. B 44, 5977 (1991).Google Scholar
7. Coehoorn, R., Phys. Rev. B 44, 9331 (1991).Google Scholar
8. Ortega, J. E. and Himpsel, F. J., Phys. Rev. Lett. 69, 844 (1992). See also contributions in these proceedings.Google Scholar
9. Details of the calculations appear in Jones, B. A. and Hanna, C. B., preprint.Google Scholar
10. See Ref. 9. Delta functions or finite-width barriers for the interfaces give a phase slip; that is, the whole RKKY curve is shifted to the left or to the right. However, no new oscillation periods appear (because the number of bound states, if present, does not vary with the width of the spacer layer). A “negative well” shows similar phase slip effects.Google Scholar