Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-27T01:46:16.641Z Has data issue: false hasContentIssue false
  • English
  • Français

Electromagnetic Waves Through Disordered Systems: Comparison of Intensity, Transmission and Conductance

Published online by Cambridge University Press:  17 March 2011

Fredy R Zypman  and
Gabriel Cwilich
Fredy R Zypman
Affiliation:
Yeshiva University, Department of Physics, New York, NY 10033
Gabriel Cwilich
Affiliation:
Yeshiva University, Department of Physics, New York, NY 10033
Get access

Abstract

We obtain the statistics of the intensity, transmission and conductance for scalar electromagnetic waves propagating through a disordered collection of scatterers. Our results show that the probability distribution for these quantities x, follow a universal form, YU(x) = xne−xμ. This family of functions includes the Rayleigh distribution (when α=0, μ=1) and the Dirac delta function (α →+ ∞), which are the expressions for intensity and transmission in the diffusive regime neglecting correlations. Finally, we find simple analytical expressions for the nth moment of the distributions and for to the ratio of the moments of the intensity and transmission, which generalizes the n! result valid in the previous case.

Type
Research Article
Information
MRS Online Proceedings Library (OPL) , Volume 694: Symposium K – Microphotonics 2001–Materials, Physics and Applications , 2001 , K5.8
Copyright
Copyright © Materials Research Society 2002

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1 Rayleigh, J. W. Strutt Lord, Phil. Mag. 47, 375 (1899)Google Scholar
2 Chandrasekhar, S., “Radiative Transfer”, Dover publishing, New York (1960)Google Scholar
3 Anderson, P. W., Phys. Rev. 109, 1492, (1958)Google Scholar
4 Abrahams, E., Anderson, P.W., Licciardello, D. C., Ramakrishnan, T.V., Phys. Rev. Lett. 42, 673 (1979)Google Scholar
5 Stephen, M., Phys. Rev. Lett. 56,1809–1810 (1986)Google Scholar
6 Albada, M. P. van, Lagendijk, A., Phys. Rev. Lett. 55, 2692–2695 (1985)Google Scholar
7 Lee, P.A., in STATPHYS 16, (Stanley, H. E., ed.), North Holland, Amsterdam, 169–174 (1986).Google Scholar
8 Cwilich, G. and Fu, Y., Phys. Rev. B46, 12015–12018 (1992)Google Scholar
9 Albada, M. P. van, Tiggelen, B.A. van, Lagendijk, Ad, Tip, Adriaan, Phys. Rev. Lett. 66, 3132–3135 (1991)Google Scholar
10 Stone, A.D., Phys. Rev. Lett. 54, 2692–2695 (1985)Google Scholar
11 Webb, R.A., Washburn, S., Umbach, C.P., and Laibowitz, R.B., Phys. Rev. Lett. 54, 2696–2699 (1985).Google Scholar
12 Garcia, N., Genack, A. Z., Phys. Rev. Lett. 63,1678–1681 (1989)Google Scholar
13 Soukulis, C., in Diffuse Waves in Complex Media (Fouque, J. P. ed.), Kluwer, 93–107 (1998).Google Scholar
14 Yablonovitch, E., Leung, K.M., Nature 401, 539 (1999)Google Scholar
15 Fink, Mathias, Physics Today 50, 34 (1997)Google Scholar
16 Campillo, M., Margerin, L. and Shapiro, N.M., in Diffuse Waves in Complex Media, (Fouque, J.P. ed.) Kluwer, 383–404 (1999)Google Scholar
17 Beenakker, C.W.J., Phys. Rev. Lett. 81, 1829–1832 (1998)Google Scholar
18 Wiersma, D.S., Albada, M.P. van, Lagendijk, A., Nature 373, 203–204 (1995).Google Scholar
19 Wang, L., Appl. Optics 32, 5043 (1993) L. Wang, P.P. Ho, C. Liu, Science 253, 769 (1991)Google Scholar
20 Kaiser, R., in Diffuse Waves in Complex Media, (Fouque, J.P. ed.), 249–288, Kluwer (1999)Google Scholar
21 Wiersma, D.S., Bartolini, P., Lagendijk, Ad, Righini, R., Nature 390, 671–673 (1997)Google Scholar
22 Kogan, E., Kaveh, M., Phys. Rev. B52, R3813–R3815 (1995); Kogan, E., Baumgartner, R. and Berkovits, R., Physica A200, 469 (1993); Kogan, M. Kaveh, R. Baumgartner, R. Berkovits, Phys. Rev. B48, 9404-9410 (1993)Google Scholar
23 Cwilich, G., in OSA Proc. on Adv. in Opt. Imaging and Photon Migration (Alfano, R., ed.), 21 (1994)Google Scholar
24 Stoytchev, M., Genack, A.Z., Phys. Rev. Lett. 79, 309 (1997)Google Scholar
25 Sebbah, P., Legrand, O., Tiggelen, B. A. van, and Genack, A. Z., Phys. Rev. E56, 3619–3623 (1997)Google Scholar
26 Chabanov, A.A., Stoychev, M. and Genack, A.Z., Nature 404, 850–853 (2000); M. Stoytchev, A.Z. Genack, Opt. Lett. 24, 262 (1999)Google Scholar
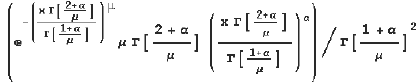27The properly normalized distribution is given by where Γ(x) stands for the Gamma function.Google Scholar
28 Cwilich, Gabriel, Zypman, Fredy R, “Transmittance quantities probability distributions of waves through disordered systems”, in Advances in Materials Theory and Modeling--Bridging Over Multiple-Length and Time Scales, Editors Vasily Bulatov, Fabrizio Cleri, Luciano Colombo, Laurent Lewis, Normand Mousseau, p 66–71 (2001)Google Scholar
29Suggested by Genak, A.Z., private communication.Google Scholar