Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-25T04:52:20.887Z Has data issue: false hasContentIssue false
  • English
  • Français

Effective Direct Piezoelectric Constants in Epitaxial Ferroelectric Films as MEMS Sensors

Published online by Cambridge University Press:  01 February 2011

Jun Ouyang ,
R. Ramesh  and
A. L. Roytburd
Jun Ouyang
Affiliation:
Materials Research and Science Engineering Center, Dept. of Materials Science and Engineering, University of Maryland, College Park, MD, 20742.
R. Ramesh
Affiliation:
Materials Research and Science Engineering Center, Dept. of Materials Science and Engineering, University of Maryland, College Park, MD, 20742. Current address: Dept. of Materials Science and Engineering, University of California, Berkeley, CA 94720-1760.
A. L. Roytburd
Affiliation:
Materials Research and Science Engineering Center, Dept. of Materials Science and Engineering, University of Maryland, College Park, MD, 20742.
Get access

Abstract

Following our previous work on the converse piezoelectric constant- 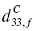in epitaxial ferroelectric films for MEMS actuator applications, the orientation dependence of the direct piezoelectric constants 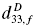, 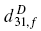and 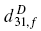are generally formulated, which can help to predict and optimize the performance of piezoelectric MEMS sensor devices based on ferroelectric thin films. Numerical results are obtained and discussed for Pb(ZrxTi1-x)O3 thin films grow on Si substrates with various compositions and structures.

Type
Research Article
Information
MRS Online Proceedings Library (OPL) , Volume 881: Symposium CC – Coupled Nonlinear Phenomena Modeling and Simulation for Smart, Ferroic and Multiferroic Materials , 2005 , CC5.7
Copyright
Copyright © Materials Research Society 2005

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1 Ouyang, Jun, Yang, S.-Y., Chen, L., Ramesh, R. and Roytburd, A. L., Appl. Phys. Lett. 85, 278 (2004).Google Scholar
2 Polla, D. L., Francis, L. F., MRS Bull., July, 59, (1996).Google Scholar
3 Nemirovsky, Y., Nemirovsky, A., Muralt, P., and Setter, N., Sens. Actuators A 56, 239 (1996).Google Scholar
4 Bernstein, J. J., Finberg, S. L., Houston, K., Niles, L. C., Chen, H. D., Cross, L. E., Li, K. K., and Udayakumar, K., IEEE Trans. Ultrason. Ferroelectr. Freq. Control 44, 960 (1997).Google Scholar
5 Muralt, P., J. Micromech. Microeng. 10, 136 (2000).Google Scholar
6 Lefki, K. and Dormans, G. J. M., J. Appl. Phys. 76, 1764 (1994).Google Scholar
7 Barzegar, A., Damjanovic, D., Ledermann, N. and Muralt, P., J. Appl. Phys. 93 (8), 4756 (2003).Google Scholar
8 Trolier-McKinstry, S., Muralt, P., J. Electroceramics, 12, 7 (2004).Google Scholar
9 Orlov, S. S. and Indenbom, V. L., Kristallografiya 14, 780 (1960); Soviet Phys.-Cryst. 14, 675(1970).Google Scholar
10 Roytburd, A. L., Phys. Stat. Sol. (a) 37, 329 (1976).Google Scholar
11 Roytburd, A. L., J. Appl. Phys. 83, 228 (1998).Google Scholar
12 Nye, J. F., Physical Properties of Crystals, Oxford 1957.Google Scholar
13 Ouyang, Jun, Ramesh, R. and Roytburd, A. L., Appl. Phys. Lett. 86, 152901 (2005).Google Scholar
14 Haun, M. J., Furman, E., Jiang, S. J. and Cross, L. E., Ferroelectrics 99, 13–86 (1989).Google Scholar
15 Freire, J. D. and Katiyar, R. S., Phys. Rev. B, 37, 2074 (1988). The following elastic compliances are calculated from it's elastic stiffness data for PT single crystal. , Google Scholar
16 Hellwege, K.-H. and Springer, A. M. Hellwege, Numerical Data and Functional Relationships in Science and Technology, Landolt-Börnstein, Berlin, 1981, 16, 123. Pseudo-tetragonal elastic compliances were given as function of x for bulk Pb(ZrxTi1-x)O3 materials near the morphotropic phase boundary (x=0.48~0.6). For rhombohedral PZT (x≥0.52), the compliance data were obtained by the following procedures as described in Ref. 18: the average value of and was used as , the average value of and was used as , and the average value of and was used as in the pseudo-cubic coordinate system. Then the cubic axis system was rotated to the rhombohedral axis system and the elastic compliance data were obtained by rules of tensor operations12 for the calculation of elastic modulus.Google Scholar
17 Hellwege, K.-H. and Springer, A. M. Hellwege, Numerical Data and Functional Relationships in Science and Technology, Landolt-Börnstein, Berlin, 1981, 16, 3. The following elastic compliances are used: .Google Scholar
18 Du, X.-H., Belegundu, U. and Uchino, K., Jpn. J. Appl. Phys., 36, 5580 (1997).Google Scholar
19 Ledermann, N., Muralt, P., Baborowski, J., Gentil, S., Mukati, K., Cantoni, M., Seifert, A., and Setter, N., Sens. Actuators, A 105, 162 (2003).Google Scholar