Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-05T04:54:41.518Z Has data issue: false hasContentIssue false
  • English
  • Français

Crossover between Ferroelectric and Quantum Paraelectric in SrTiO3 both by Isotopic Substitution and Hydrostatic Pressure

Published online by Cambridge University Press:  01 February 2011

Ruiping Wang  and
Mitsuru Itoh
Ruiping Wang
Affiliation:
Smart Structure Research Center, National Institute of Advanced Industrial Science and Technology, Tsukuba Central 2, 1-1-1, Umezono, Tsukuba, 305-8568, Japan
Mitsuru Itoh
Affiliation:
Materials and Structures Laboratory, Tokyo Institute of Technology, 4259 Nagatsuta, Midori, Yokohama, 226-8503, Japan
Get access

Abstract

Quantum paraelectric SrTiO3 undergoes a transition to ferroelectric by the substitution of 18O for 16O. The Tc vs. x in SrTi(16O1-x18Ox)3 follows Tc = 30.4(x - 0.33)1/2. Application of the hydrostatic pressure on the SrTiO3 and SrTi(16O0.0718O0.93)3 have the effects of decreasing ε and depressing Tc, respectively. Above the critical pressure pc, ferroelectricity of SrTi(16O0.0718O0.93)3 disappears. Fitting the data to the Barrett's formula, ε 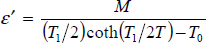, elucidated that T0 and T1 for both compounds changes linearly with pressure.

Type
Research Article
Information
MRS Online Proceedings Library (OPL) , Volume 718: Symposium D – Perovskite Materials , 2002 , D8.8
Copyright
Copyright © Materials Research Society 2002

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Bednorz, J. G. and Müller, K. A., Phys. Rev. Lett., 52, 2289 (1984).Google Scholar
2. Kleemann, W., Int. J. Mod. Phys., 7, 2469 (1993).Google Scholar
3. Lemanov, V. V., Smirnova, E. P., and Tarakanov, E. A., Phys. Solid State, 37, 1356 (1995).Google Scholar
4. Lemanov, V. V., Smirnova, E. P., and Tarakanov, E. A., Phys. Rev. B, 54, 3151 (1996).Google Scholar
5. Markovin, P. A., Lemanov, V. V., Korshunov, O.Yu., and Kleemann, W., Feroelectrics, 199, 121 (1996).Google Scholar
6. Lemanov, V. V., Smirnova, E. P., and Tarakanov, E. A., Phys. Solid State, 39, 1468 (1997).Google Scholar
7. Lemanov, V. V., Phys. Solid State, 39, 1468 (1997).Google Scholar
8. Markovin, P. A., Lemanov, V. V., and Guzhva, M. E., Ferroelectrics, 184, 269 (1996).Google Scholar
9. Guzhva, M. E., Lemanov, V. V., Markovin, P. A., and Shuplygina, T. A., Ferroelectrics, 218, 93 (1998).Google Scholar
10. Lemanov, V. V., Ferroelectrics, 226, 133 (1999).Google Scholar
11. Wang, R., Inaguma, Y., and Itoh, M., Mat. Res. Bull., 36, 1693 (2001).Google Scholar
12 Höchli, U. T., Weibel, H. E., and Boatner, L. A., Phys. Rev. Lett., 39, 1158 (1977).Google Scholar
13. Höchli, U. T., Knorr, K., and Loidl, A., Adv. Phys., 39, 405 (1990).Google Scholar
14. Vugmeister, B. E. and Glinchuk, M. D., Rev. Mod. Phys., 62, 993 (1990).Google Scholar
15. Hanske-Petipierre, O. and Yocoby, Y., and Leon, J. Mustre de, Phys. Rev. B, 44, 6700 (1991).Google Scholar
16. Akimov, I. A., Sirenko, A. A., and Clerk, A. M., Phys. Rev. Lett., 84, 4625 (2000).Google Scholar
17. Khmel'ninskii, D. E. and Shneerson, V. L., Sov. Phys. Solid State, 13, 687 (1971).Google Scholar
18. Oppermann, R. and Thomas, H., Z. Phys. B, 22, 387 (1975).Google Scholar
19. Schneider, T. S., Beck, H., and Stoll, E., Phys. Rev. B, 13, 1123 (1976).Google Scholar
20. Morf, R., Schneider, T., and Stoll, E., Phys. Rev. B, 16, 462 (1977).Google Scholar
21. Kvyatkovskii, O. E., Phys. Solid State, 43, 140 (2001).Google Scholar
22. Itoh, M., Wang, R., Inaguma, Y., Yamaguchi, T., Shan, Y-J., and Nakamura, T., Phys. Rev. Lett., 82, 3540 (1999).Google Scholar
23. Itoh, M. and Wang, R., Appl. Phys. Lett., 76, 221 (2000).Google Scholar
24. Wang, R. and Itoh, M., Phys. Rev. B. 64, 174104 (2001).Google Scholar
25. Wang, R. and Itoh, M., Phys. Rev. B, 62, R3577 (2000).Google Scholar
26. Kvyatkovskii, O. E., Solid State Commun., 117, 455 (2001).Google Scholar
27. Kim, I-S., Itoh, M., and Nakamura, T., Solid State Commun., 101, 77(1992).Google Scholar