Published online by Cambridge University Press: 29 November 2013
A long deoxyribose-nucleic-acid (DNA) molecule can be seen directly under an optical microscope if it is suitably decorated by fluorescent dyes. This makes it possible to see how a long chain responds to external forces f. The conformation of a uniformly stretched chain has been discussed by Pincus. Under a force f, acting on the two free ends, the chain configuration is modified only above a scale length ξ = kT/f where T is temperature and k is Boltzmann's constant. The chain (Figure 1a), containing N monomers, can be pictured as a string of blobs of size ξ containing g monomers with ξ = gva, where a is the monomer size (v = 1/2 in a θ solvent: the chain is ideal, v = 3/5 in a good solvent). The end-to-end distance is L = (N/g)ξ, that is,
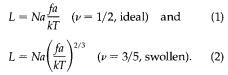
For DNA, which is a semirigid chain, ideal behavior has been observed for chain lengths up to 20 μm when f is small. At higher f ( ≅ 100 pN), Cluzel et al. found a structural phase transition, corresponding to a plateau in the curve f versus elongation. Going even further, one reaches the break point.
Another method to stretch DNA is based on optical tweezers. Here one end of the DNA is attached to a bead of glass of high polarizability, which is attracted by a region of large (optical) electric field. This was used by the Stanford group: In one series of experiments, they observed the conformations of the chain, pulled at one end by a constant force f. The friction on monomers are cumulative, and the tension along the chain is not uniform—it increases from the free end to the tethered end.