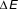Introduction
Ferromagnetic nanomaterials are considered to be at a critical size d cr such that the particles form single magnetic domains. Below this threshold, which is most often <20 nm, the properties become size-dependent. Reference Stoner and Wohlfarth1–Reference Batlle and Labarta5 In simple models of monodomain magnets, all of the atomic spins are parallel. Real magnetic nanoparticles are more complex, and questions remain regarding numerous fundamental issues. The atomic spins at the surface of a particle may behave differently than those in the bulk, with different magnetic moments, Reference Curiale, Granada, Troiani, Sanchez, Leyva, Levy and Samwer6–Reference Salafranca, Gazquez, Pérez, Labarta, Pantelides, Pennycook, Batlle and Varela9 different anisotropy, Reference Mørup10,Reference Yanes, Chubykalo-Fesenko, Kachkachi, Garanin, Evans and Chantrell11 or different orientation due to surface spin canting. Reference Kodama, Berkowitz, McNiff and Foner12 The surface spins may be chemically distinct from those in the core, and if they form a second magnetic phase, there can be exchange bias or exchange spring effects, where the proximity of two magnetically ordered phases alters the switching field and reversibility. Reference Skumryev, Stoyanov, Zhang, Hadjipanayis, Givord and Nogues13 One of the biggest challenges is in preparing uniform nanoparticles that enable these questions to be addressed. This involves not only improved size control, but also a reduction in the impurity and defect density, as well as thorough characterization of the resulting materials.
Even though models of ideal monodomain magnets were developed over 50 years ago, Reference Stoner and Wohlfarth1–Reference Brown3 magnetic nanoparticles continue to be of great research interest. As with other areas of nanotechnology, the field of magnetic nanoparticles has a history of both great hype and difficulties in implementation. Nonetheless, the unique properties of nanoscale magnetic materials provide an opportunity for fundamental investigations, present key building blocks to create more complex structures, and provide opportunities for applications ranging from chemical sensors to therapeutic devices.
We focus on small magnetic nanoparticles prepared by chemical means that can be dispersed in liquids and moved by external forces. Top-down techniques, such as mechanical milling, result in particles with size distributions too broad for the applications discussed in this special issue. We focus on chemical methods because they provide reasonable amounts of material (milligrams to grams) with good monodispersity and chemical uniformity. The ability to disperse and move magnetic nanoparticles is a key advantage for many current and potential applications of magnetic nanoparticles. Iron oxide nanoparticles are now embedded in cellulose fibers used in paper money as an anti-counterfeiting measure. If you hold a strong permanent magnet close to a recently printed US one dollar bill, you can observe a deflection. This idea has also been used to prepare magnetically responsive paper, Reference Olsson, Azizi, Salazar-Alvarez, Belova, Ström, Bergland, Bokala, Nogues and Gedde14 magnetic toner for copying machines, Reference Ziolo, Giannelis, Weinstein, O’Horo, Ganguly, Mehrotra, Russell and Huffman15 magnetic hydrogel composites, Reference Ramanujan and Lao16,Reference Xu, Majetich and Asher17 and micron-sized polymer beads embedded with magnetic nanoparticles. Reference Zhao, Saatchi and Hafeli18 In all cases, the fact that the particles are small and mobile enables them to be incorporated into a larger structure and make the overall structure magnetically responsive. Magnetic nanoparticles are being intensively studied for medical imaging, therapy, and drug delivery Reference Pankhurst, Connolly, Jones and Dobson19–Reference Krishnan21 because static magnetic fields do not interfere with biological function, unlike large electric fields, which can stimulate nerve endings or open channels in cell membranes.
The field of magnetic nanostructures is broad, and the articles in this issue of MRS Bulletin focus on a subset of what may be considered as magnetic nanoparticles. However, the concept of monodomain magnets has been used to understand a wide range of materials, including granular CoCrPt/SiO x media used in hard disk drives, Reference Terris and Thomson22 soft nanocrystalline alloys where exchange coupling of randomly oriented magnetic grains reduces the overall anisotropy, Reference Herzer23,Reference Makino, Hatani, Naitoh, Bitoh, Inoue and Masumoto24 and the free magnetic layer of a multilayer nanopillar that can be switched by a spin polarized current. Reference Katine, Albert, Buhrman, Myers and Ralph25 Monodomain magnets are under investigation for use as individual bits of information in what is known as bit patterned media. Reference Yang, Chen, Huang, Duan, Thiyagarajah, Hui, Leong and Ng26,Reference Albrecht, Hu, Guhr, Ulbrich, Boneberg, Leiderer and Schatz27 We have omitted lithographically patterned submicron structures Reference Pardavi-Horvath, Ng, Castano, Köner, Garcia and Ross28–Reference Gubbiotti, Tacchi, Madami, Carlotti and Adeyeye30 and magnetic nanowires, Reference Maqableh, Huang, Sung, Madhukar Reddy, Norby, Victora and Stadler31,Reference Rossa, Vivas, Pirota, Asenjo and Vazquez32 though their properties are similar to the particles discussed here. There have been other reviews on such related topics in magnetic nanostructures, Reference Bader33–Reference Martin, Nogues, Liu, Vincent and Schuller39 and the interested reader is encouraged to consult them.
We begin with a short description of the physics that unifies the field of magnetic nanoparticles and enables comparison of different materials. Next we provide an overview of current trends and identify specific challenges for applications of magnetic nanoparticles. The articles in this issue include detailed accounts of the current trends in specific topical areas related to magnetic nanoparticles and their applications.
Materials design of monodomain magnetic nanoparticles
In spherical particles, the maximum monodomain size d cr ranges from ∼20 to several hundred nm. It can be estimated from the parameters of the magnetic material, Reference McCurrie40 including the saturation magnetization M s, the exchange stiffness A, and the anisotropy K. The saturation magnetization M s depends on the density of magnetic atoms and their magnetic moments. The exchange stiffness A favors parallel spins and is proportional to the Curie temperature of the bulk material. For a face-centered cubic lattice with lattice parameter a and exchange energy 2JS Reference Jacobs, Bean, Rado and Suhl2 , A = 4JS 2/a, J is the exchange constant and S is the spin of the magnetic atom or ion. Unless the material is amorphous, there will be magnetocrystalline anisotropy K u due to spin-orbit coupling, and there will be minimum energy when the magnetization lies along a particular crystallographic direction, called the easy axis. Figure 1 shows the magnetization for a single particle.

Figure 1. (a) A spherical particle has a net magnetic moment with magnitude μ = M s V, where V is the particle volume and M s is the saturation magnetization, due to the internal alignment of atomic spins. In the case of a perfect sphere, it behaves as a point dipole. (b) The equilibrium direction of the single particle magnetization depends on the external magnetic field H and also on its magnetocrystalline anisotropy easy axis. Note: M is the magnetization, φ is the angle between the magnetization and the easy axis, and θ is the angle between the easy axis and the applied field.
In single domain particles, the exchange-coupled spins rotate in unison, flipping the entire particle’s magnetic moment coherently. The switching field or coercivity, H c, is a maximum for particles at the largest monodomain size Reference Luborsky41 and can be predicted from an energy barrier model, Reference Sharrock42 as illustrated in Figure 2 .

Figure 2. The energy (E) of a magnetic nanoparticle as a function of the magnetic moment orientation relative to the external field direction (H). Because of the magnetocrystalline anisotropy, there will be an energy barrier between “spin up” and “spin down” states (black circles with green arrows), even for an isolated particle. When H = 0,
![]() $\Delta E$
= KV. When particles interact, there is still an energy barrier, but its magnitude changes. When the thermal energy is high, relative to the energy barrier height, equilibration is rapid. Note: K is the anisotropy; V is the particle volume, M
s is the saturation magnetization, k
B is the Boltzmann constant, T
high is a higher temperature, and T
low is a lower temperature.
$\Delta E$
= KV. When particles interact, there is still an energy barrier, but its magnitude changes. When the thermal energy is high, relative to the energy barrier height, equilibration is rapid. Note: K is the anisotropy; V is the particle volume, M
s is the saturation magnetization, k
B is the Boltzmann constant, T
high is a higher temperature, and T
low is a lower temperature.
The rate of equilibration will depend on ΔE/k B T (where ΔE is the height of the energy barrier for coherent rotation of the particle moment, k B is the Boltzmann constant, and T is the temperature) and on the Larmor precession frequency of the magnetic moment about the applied field H. The measured magnetization also depends on the measurement time. If the sample has equilibrated within the measurement time, typically ∼100 s, it is said to be superparamagnetic. The effects of temperature and measurement time on the magnetization curves are shown in Figure 3 . Here an external magnetic field H is applied, and the material magnetization, or magnetic moment density, M, parallel to the applied field is measured. The saturation magnetization M s occurs when the spins of the ferromagnet are fully aligned. When the magnetic field is turned off following saturation, the sample has a remanent magnetization M r at H = 0. To reduce the magnetization to zero, a magnetic field must be applied in the opposite direction. This is known as the coercive field or coercivity H c.

Figure 3. Magnetization (M) as a function of the applied magnetic field (H). (a) Superparamagnetic particles have zero coercivity. This occurs either when the thermal energy is high, relative to the energy barrier, or when the measurement time (t meas) is long so that the sample reaches thermal equilibrium. (b) If equilibrium is not reached within the measurement time, then hysteresis will be observed. Note: k B is the Boltzmann constant, T high is a higher temperature, and T low is a lower temperature.
As the size of a monodomain particle is reduced, H c drops until it reaches zero at the superparamagnetic limit d SP. An ensemble of particles is said to be superparamagnetic if they were originally aligned but have random directions at the measurement time, due to thermal fluctuations of energy k B T. An individual particle at any instant of time will still have a magnetic moment, but the average of the magnetic moments, and therefore the magnetization M, will be zero in zero applied field. Superparamagnets have an S-shaped magnetization curve M(H) (Figure 3a) proportional to a Langevin function. The dynamics of relaxation for superparamagnets are predicted by the Néel model; Reference Brown3,Reference Brown43–Reference Néel45 an ensemble of identical, non-interacting particles has a magnetization that decays exponentially with time. However, in real systems, there are deviations from this prediction even with ∼1 volume percent magnetic nanoparticles, Reference Zhang, Boyd and Luo46 which have been attributed to long-range magnetostatic interactions between particles. Figure 4 shows the values of d cr and d SP for common magnetic materials.

Figure 4. Threshold diameters for superparamagnetism (d sp) and maximum monodomain (d cr) size for spherical nanoparticles, based on bulk material parameters. (Data taken from References 21 and 40.) The measurement time is assumed to be ∼100 s. The size of the particles has a significant impact on the properties of these materials and should be carefully controlled to meet the needs of a given application.
The same particles may be superparamagnetic at one temperature and show hysteresis at a lower temperature. If superparamagnetic particles are cooled, at some temperature the measurement time will be insufficient for complete magnetic relaxation. This temperature is known as the blocking temperature, T b. Below T b, magnetic nanoparticles exhibit hysteresis due to metastability rather than domain wall motion. At the blocking temperature, the magnetic moments of different particles are randomly oriented by thermal excitations. As shown in Figure 5 , this is different from the Curie temperature T C, where the spins within individual particles are randomized by the thermal energy; in general, T b << T C .

Figure 5. Comparison of blocking temperature (T b) and Curie temperature (T C). Below the blocking temperature, there is some net alignment of the particle spins, while above it, the spins are in random directions. Below the Curie temperature, there is some net alignment of the atomic spins within a particle, while above it, they are randomized.
A magnetic particle placed in a uniform magnetic field will rotate due to the magnetic torque. This is referred to as Brownian rotation, as opposed to Néel rotation where the particle is fixed in space but its magnetization direction rotates. To move the particle, a spatially varying magnetic field is necessary. The magnetic force is given by
![]() ${F_m}\, = \,({M_s}V\cdot \nabla )H$
, where M
s is the saturation magnetization, and V is the particle volume.
${F_m}\, = \,({M_s}V\cdot \nabla )H$
, where M
s is the saturation magnetization, and V is the particle volume.
Preparation of magnetic nanoparticles
There are several synthetic routes for the production of magnetic nanoparticles, but they can be divided into two broad classes. Aqueous methods such as coprecipitation Reference Massart and Cabuil47,Reference Tartaj, Morales, Veintemillas-Verlaguer, Gonzalez-Carreno and Serna48 and hydrothermal approaches Reference Adschiri, Lee, Goto and Takami49–Reference Togashi, Naka, Asahina, Sato and Takami51 produce rougher and less monodisperse particles, but the particles are more likely to be biocompatible and can be fabricated in large (100s of g) quantities. Reference Stone, Hipp, Barden, Brown and Mefford52 To maintain this suspension for usable periods of time, the surface of the particles must contain a stabilizing layer to provide sufficient steric repulsion to overcome van der Waals attractive forces between particles. Alternatively, non-aqueous methods Reference Petit, Taleb and Pileni53–Reference Mayo, Yavuz, Yean, Cong, Shipley, Yu, Falkner, Kan, Tomson and Colvin62 can generate highly monodisperse particles that are stabilized with hydrophobic surfactants. However, for biomedical applications, the surface of the particles must be modified by a water-soluble polymeric material to provide steric stability as well as biocompatibility. While some materials such as CoFe2O4 and FePt offer superior magnetic saturation (M s) and anisotropy values, Reference Colombo, Carregal-Romero, Casula, Gutiérrez, Morales, Böhm, Heverhagen, Prosperi and Parak63–Reference Tterlikkis and Jenkins67 their toxicity may be of concern. Reference Laurent, Dutz, Häfeli and Mahmoudi68 Because of this, the biomedical field has focused on iron oxides. As the stabilizing layer on the surface of the magnetic nanoparticle is functionalized for a given application, the relationship of this new surface chemistry must be evaluated to determine accurate biointeractions. Reference Crist, Grossman, Patri, Stern, Dobrovolskaia, Adiseshaiah, Clogston and McNeil69
Current challenges and future directions
There are numerous challenges remaining in the understanding and application of magnetic nanoparticles. This is a highly interdisciplinary field, and the solutions are likely to come from coordinated efforts of researchers in different areas. While we have not focused on synthetic techniques, there is great need for economical large-scale preparation methods that produce nanoparticles with uniform size, shape, structure, and magnetic response. Even in small-scale syntheses, uniformity and repeatability are critical for precise studies of structure–function relationships that will benefit the optimization of particle properties, particularly the saturation magnetization.
Fundamental issues such as surface anisotropy of individual particles, composition variations within alloy particles, and magnetostatic interactions between particles all affect the magnetic response, but are not yet fully understood. In order to bridge the gap between theoretical predictions and experiments, there is a need for more nanoscale magnetic measurements on single particles or small assemblies.
It is still a major challenge to control the motion of a magnetic nanoparticle within the human body, as would be needed for magnetically guided drug delivery or hyperthermic cancer treatment. This requires both large magnetic field gradients and active control to balance the effect of blood perfusion, or cooling by blood flow. Alternatively, the particles would be guided by chemical receptors rather than by magnetic forces, but there is little information about the comparative efficiency of these approaches. Applications of magnetic nanoparticles in biomedicine have particularly complex and demanding requirements. The high salt content of biological media makes steric stabilization necessary. Reference Goon, Lai, Lim, Munroe, Gooding and Amal70–Reference Amstad, Gillich, Bilecka, Textor and Reimhult73 The nature of the surface coating affects the in vivo response—whether the particles are quickly excreted or taken up into cells, and whether they are toxic or selectively bind to particular receptors. Reference Crist, Grossman, Patri, Stern, Dobrovolskaia, Adiseshaiah, Clogston and McNeil69
Overview
In the articles in this issue of MRS Bulletin, Evans et al. review simulations of the magnetization patterns within a nanoparticle and show the effect of surfaces, interfaces, and local variations on chemical composition. Some of the articles focus on magnetic forces on nanoparticles. Tracy and Crawford discuss magnetically guided self-assembly for pattern formation. Odenbach describes how magnetic fields can move a ferrofluid droplet and change its viscosity. He then discusses applications of ferrofluids in loudspeakers and rotary feedthroughs. Kozissnik and Dobson describe biomedical applications, including cell separation, drug targeting, and gene transfection, which rely on the ability to move the particles with a field gradient, and magnetic hyperthermia cancer treatment, which is based on energy dissipation in a high-frequency magnetic field. In their article, Moreland et al. describe how the magnetic moments of nanoparticles are used for in vivo imaging, both in magnetic resonance imaging and the new field of magnetic particle imaging. Here the particles are not moved magnetically, but the fields they generate within tissue are used to sense the local environment. Finally, while spintronics has been a dominant theme in research on magnetic materials for many years, Markovich describes how the spintronics of magnetic nanoparticles has been investigated only recently. Together these articles provide a broad perspective on current research trends, emerging directions, and future applications.