Introduction
The discovery and development of new metallic alloys with unique properties and functionalities have revolutionized entire industries (e.g., aviation, space, communications, automotive, biomedical, and architecture), continuing the centuries-long trend for materials to fundamentally transform society (i.e., the bronze, iron, and silicon ages). Their design has traditionally been experimentally intensive, with linear exploration of composition space or via “design of experiments” approaches. Often with five to 10 major elements and as many “minor” elements, the compositional landscape is prohibitively large. Thus the design and development process has been slow and expensive, and more recently, unable to keep pace with the design tools of other engineering disciplines.Reference Pollock, Allison, Backman, Boyce, Gersh, Holm, LeSar, Long, Powell, Schirra, Whitis and Woodward1–Reference Banerjee and Williams5
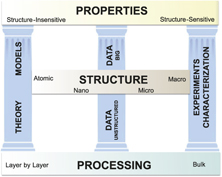
To a greater degree than many other classes of materials, metallic alloys are challenged by a strong interdependence of processing, structure, and properties (PSP) across length scales, from atomic (Å) to the nanoscale (nm), spanning the microscale (μm) and extending up to the macroscale (>mm) (Figure 1). In order to reliably produce materials that perform in a predictable manner in service, it is essential for the PSP linkages to be predictable. These linkages have traditionally been established via experiments and characterization. For example, as demonstrated by the right pillar of Figure 1, the influence of forging parameters on grain structure and texture and the resultant yield strength and fatigue life of an alloy would be understood by varying temperatures and strain rates during forging, measuring grain size and texture by electron backscatter imaging in a scanning electron microscope (SEM), and machining test specimens to establish yield strength and S-N curves as a function of temperature. Characterization results, processing information, and the results of testing would be stored in different data formats, most likely without metadata and in different physical locations.
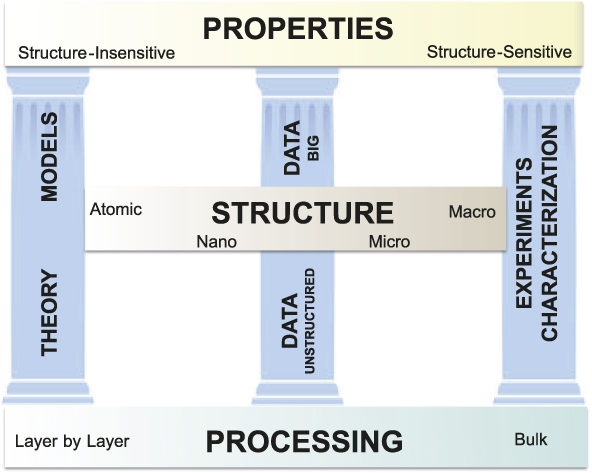
Figure 1. The alloy design infrastructure, where processing–structure–property (PSP) relationships are derived from three pillars of materials science: theory and models/simulations; data (unstructured and high volume “big” data); and experiments and characterization.
In recent years, there has been a dramatic expansion in our ability to predict PSP relationships, through improved theory, expanding suites of models, and a dramatic expansion in our ability to generate, archive, federate, and analyze materials data.Reference Pollock, Allison, Backman, Boyce, Gersh, Holm, LeSar, Long, Powell, Schirra, Whitis and Woodward1–Reference de Pablo, Jones, Lind, Ozolins and Ramirez3,Reference Warren6,Reference Kalidindi and De Graef7 These emerging capabilities provide two additional foundational “pillars” (Figure 1) that promise to dramatically change the landscape for alloy design. New developments along all three pillars (theory/modeling, data, and experiments/characterization) have been in large part enabled by an unprecedented expansion in computational power over the past decade. Thus, the aspirational vision to design new alloys “on demand” with the ability to predict their properties within statistically significant confidence limits is now within reach. In this article, we highlight examples of the progress along each of the pillars and also call attention to some of the many remaining gaps in the infrastructure.
Theory and computation
Most alloys are designed to harness the multitude of structure-sensitive properties that can be engineered over different length scales (Figure 2).Reference Natarajan and Van der Ven9 A multiscale approach is crucial, and modeling in the context of alloy design must be capable of predicting properties over scales that range from the electronic structure to the macroscopic continuum scale. There are two general classes of multiscale materials theories: (1) those that address thermokinetic properties, of relevance to develop processing strategies; and (2) those that seek to predict mechanical properties.
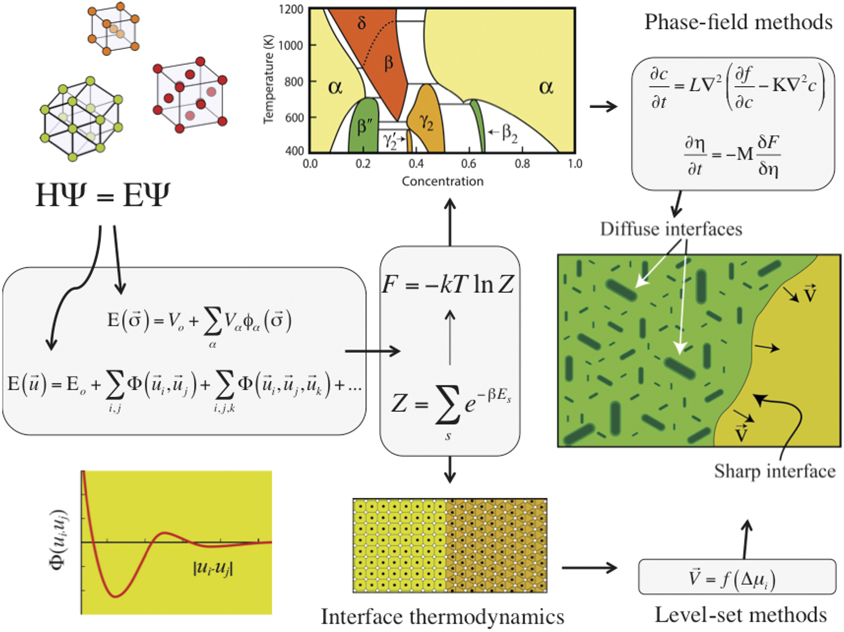
Figure 2. A multiscale approach that connects the electronic structure of a solid to its thermodynamic and kinetic properties at the macroscale. Approximations to the Schrödinger equation inform effective Hamiltonians and force-field descriptions, which in turn, are used in Monte Carlo and molecular dynamics simulations to calculate thermodynamic potentials and kinetic coefficients. These then feed into mesoscale phenomenological descriptions of microstructure evolution and phase transformations, such as the phase-field model and sharp interface approaches.Reference Natarajan and Van der Ven9
Thermodynamic prerequisites
An essential ingredient of any alloy development effort is an accurate description of thermodynamic properties within the composition design space. An alloy designer is generally keen to know whether targeted phases are thermodynamically stable or metastable. The article by Raabe et al. in this issue, for example, describes new alloy design approaches that specifically exploit metastability.Reference Raabe, Li and Ponge8 The CALculation of PHAse Diagrams (CALPHAD) method was an early attempt to organize the vast experimental thermochemical data of known alloys and compounds within a thermodynamically self-consistent framework.Reference Sundman, Chen and Du10,Reference van de Walle and Asta11 It has served as an invaluable tool in alloy design as it enabled the rapid and flexible calculation of thermodynamic properties and phase diagrams. In its original incarnation, the method was based solely on experimentally measured data, making it essentially an interpolation tool.
The emergence of accurate and easy to use first-principles electronic structure methods have given alloy designers a new tool with which to survey previously unexplored composition spaces. First-principles electronic methods can predict formation enthalpies for any candidate crystal structure, often with remarkable accuracy.Reference Lejaeghere, Bihlmayer and Bjoerkman12 While such calculations do not account for the effects of temperature explicitly, they can be used to construct zero-Kelvin phase diagrams, and thereby reveal whether particular intermetallic compounds are stable or not, at least at low temperature. First-principles methods have become so robust in recent years that they can be implemented in high-throughput schemes to map out materials properties over vast uncharted composition spaces. Efforts that seek to do this systematically include the Materials Project, the Open Quantum Materials Database (OQMD), Automatic Flow for Materials Discovery (AFLOW), and the Novel Materials Discovery Laboratory (NOMAD), which are large interactive repositories of materials properties that have been calculated with density functional theory.Reference Tanaka, Rajan and Wolverton13–Reference Draxl and Scheffler16
Unfortunately, the availability of powerful first-principles software packages is only a first step in developing comprehensive thermodynamic descriptions in new composition spaces. Many alloys are designed for high-temperature applications or exploit properties of solid solutions. In these circumstances, entropy plays a crucial role. The strengthening L12 phase in Co-rich Co-Al-W alloys, for example, only emerges at temperatures above 900°C, in large part due to a combination of both configurational and vibrational entropy.Reference Rhein, Dodge, Chen, Titus, Pollock and Van der Ven17 Zero-Kelvin enthalpies by themselves are, therefore, often insufficient to guide alloy developers toward promising high-temperature phases that are entropy stabilized.
Statistical mechanics approaches are necessary to calculate entropic contributions to free-energy descriptions of multicomponent alloys from first principles. A statistical mechanics study of phase stability usually requires an order of magnitude more computational effort than calculations of zero-Kelvin phase diagrams. This is due to the fact that most first-principles statistical mechanics schemes consist of a step that maps the results of large numbers of first-principles electronic structure calculations onto a computationally simpler model that can be evaluated rapidly within molecular dynamics or Monte Carlo simulations where thermodynamic averages are collected (as indicated in the left half of Figure 2). Two general approaches are common. The first relies on force-field descriptions, which in the early days were based on interatomic potentials having functional forms that were motivated by the bonding physics of particular materials classes. Machine-learning approaches are now offering more flexibility, as they do not require predetermined functional forms.Reference Behler18–Reference Drautz21 A second approach uses effective Hamiltonians that are designed to extrapolate first-principles energies for a restricted set of degrees of freedom.Reference Van der Ven, Thomas, Puchala and Natarajan22 Two well-known examples are the harmonic lattice dynamical Hamiltonians describing vibrational excitations and cluster expansion Hamiltonians describing configurational degrees of freedom. Effective Hamiltonians have proven invaluable in many first-principles studies of high-temperature thermodynamic properties, especially when configurational degrees of freedom are important as in nondilute, disordered alloys.Reference van de Walle23–Reference Gunda and Van der Ven25 They can be parameterized to have similar accuracies as those of the first-principles methods they have been trained to using one of several fitting methodsReference Van der Ven, Thomas, Puchala and Natarajan22 and are generally easier to train than the more complex force-field descriptions.
In spite of the remarkable capabilities of first-principles statistical mechanics approaches, fundamental theoretical challenges remain. One of these pertains to high-temperature phases that become dynamically unstable at low temperature. Many technologically important high-temperature materials have crystal structures that are predicted to be dynamically unstable at zero Kelvin by first-principles electronic-structure calculations. Well-known examples include cubic ZrO2 as well as body-centered-cubic Ti and Zr, among others.Reference Puchala and Van der Ven24–Reference Chen, Thomas, Natarajan and Van der Ven28 Anharmonicity must be accounted for to predict the stability of high-temperature phases with low-temperature phonon instabilities since the statistical mechanics approaches based on either the harmonic or quasi-harmonic approximation of crystal vibrationsReference van de Walle, Hong, Kadkhodaei and Sun29,Reference Fultz30 break down for these phases. This not only substantially complicates the calculation of high-temperature free energies, it also poses challenges to formulating a conceptual understanding of the thermal excitations responsible for the thermodynamic stability of many high-temperature phases. Indeed, the true nature of a dislocation or a diffusive hop remains to be established in a high-temperature phase that becomes dynamically unstable at low temperature. Zero-Kelvin estimates of elastic moduli for such phases are often meaningless, as instabilities with respect to a homogeneous distortion of the crystal results in negative elastic moduli. It is only through anharmonic vibrational excitations that such instabilities are lifted and any effort to predict mechanical properties of many high-temperature phases therefore requires a full statistical mechanics treatment.Reference Thomas and Van der Ven31–Reference Wojdel, Hermet, Ljungberg, Ghosez and Iniguez34
Several schemes have been proposed to account for the large anharmonic excitations responsible for stabilizing high-temperature phases. Some approaches attempt to treat anharmonicity directly, by using ab initio molecular dynamics,Reference Ozolins32 or indirectly via self-consistent phonon theories, which approximate the full anharmonic energy surface with a dynamically stable quasi-harmonic potential that describes vibrational excitations at the characteristic amplitudes of a specified temperature.Reference Souvatzis, Eriksson, Katsnelson and Rudin35 Other approaches rely on anharmonic lattice dynamical Hamiltonians that can be arbitrarily refined to match the energy of the crystal as a function of vibrational degrees of freedom.Reference Thomas and Van der Ven33,Reference Wojdel, Hermet, Ljungberg, Ghosez and Iniguez34 While these approaches show promise, they remain labor intensive and are generally developed on a case-by-case basis.
While challenges remain, the availability of highly automated first-principles and statistical mechanics tools is opening doors to new design approaches. For example, it is becoming easier to explore the stability of existing and hypothetical phases under more complex thermodynamic constraints than are commonly imposed. The metastability of a target phase may be turned into absolute stability upon altering thermodynamic boundary conditions. For example, an additional lever with which to manipulate relative stabilities between phases is strain.Reference Thomas and Van der Ven36 While pressure is well known to modify relative stabilities, anisotropic stress states that are present during coherent nucleation and growth can be exploited to either suppress undesirable precipitates or favor a desirable precipitate.Reference Natarajan, Solomon, Puchala, Marquis and Van der Ven37 They can also be exploited to control precipitate shapes.Reference Teichert and Garikipati38,Reference DeWitt, Solomon, Natarajan, Araullo-Peters, Rudraraju, Aagesen, Puchala, Marquis, Van Der Ven, Thornton and Allison39 Metallurgists have been aware of these notions for many decades and have exploited them in recent years to improve the mechanical properties of lightweight magnesium alloys, as described in this issue by Nie et al. in this issue.Reference Nie and Wang40 Emerging computational tools now generate new insights and provide guidance as to how strengthening phases and microstructures can be achieved.Reference Pollock4
Kinetics
Once a thermodynamic description has been mapped out in a particular composition space, it is often necessary to establish kinetic properties that describe the evolution of an alloy during both synthesis and use. Although there are many examples where dynamic processes in materials occur far from equilibrium, a large class of thermally activated, nonequilibrium processes of technological interest can be described at a phenomenological level using irreversible thermodynamics or phase-field models that were inspired by Cahn–Hilliard–Allen-type kinetic descriptions.Reference Cahn41,Reference Allen and Cahn42
Phase-field models predict the temporal evolution of a set of order parameters for nonequilibrium phenomena in microstructures consisting of phases that share a group/subgroup symmetry relationship.Reference Chen43 They can be applied to predict coherent precipitation (upper right of Figure 2), spinodal decomposition, and weak martensitic transformations. Examples of order parameters include composition (for a miscibility gap), order-disorder order parameters (e.g., to describe the γ to γ′-L12 reaction in face-centered-cubic superalloys), and displacive shuffle amplitudes and strain-order parameters (e.g., if there is a cubic to tetragonal type of transformation).Reference Van der Ven, Thomas, Puchala and Natarajan22 The various phases competing for stability correspond to local minima on a common free-energy surface that is continuous as a function of these order parameters.Reference Natarajan, Thomas, Puchala and Van der Ven44 Ingredients to a phase-field model include homogeneous free energies as a function of order parameters, gradient energy coefficients, and various mobility coefficients.
Other phenomenological methods exist to predict nonequilibrium processes in which one phase converts into another through a reconstructive mechanism (lower right of Figure 2). The interfaces separating the phases participating in a reconstructive phase transformation are often atomically abrupt, in rare circumstances coherent or possibly semi-coherent, but usually incoherent in nature. Separate free-energy descriptions are necessary for each phase. Furthermore, separate constitutive thermodynamic and kinetic descriptions are required for the interfaces separating the various phases.Reference Voorhees and Johnson45 From a numerical point of view, phase evolution involving the migration of sharp interfaces with their own separate response functions can be simulated using a level-set approach.Reference Gibou, Fedkiw and Osher46
Predicting dynamical evolution using phenomenological kinetic approaches requires accurate thermodynamic and kinetic information that is often difficult if not impossible to measure experimentally, especially in isolation. Phase-field models of microstructure evolution rely on gradient energy coefficients, which are especially difficult to measure experimentally. Here again, first-principles statistical mechanics methods and tools can play a crucial role in informing phenomenological descriptions of nonequilibrium processes in the solid state. First-principles approaches to predict atomic mobilities are now well established.Reference Van der Ven, Thomas, Puchala and Natarajan22,Reference Van der Ven, Yu, Ceder and Thornton47 Progress has also been made in identifying order parameters and in predicting free energies as a function of those order parameters.Reference Natarajan, Thomas, Puchala and Van der Ven44 Interfacial free energies and mobilities are also accessible with first-principles statistical mechanics methods.Reference Hoyt, Asta and Karma48–Reference Mishin, Asta and Li50 Many challenges remain. One is overcoming the hurdles to developing a quantitative theory of nucleation. The challenges in this respect are not just limited to developing an accurate theory of nucleation and accompanying modeling tools to predict nucleation rates, but also to develop new experimental probes that will enable more precise and in situ measurements of nucleation processes.
Mechanical properties
The thermokinetic models previously described can be hierarchically integrated within a simple multiscale framework. At the micro- and mesolength scales, there are the phenomenological descriptions, while at the atomic and nanoscale, there are the first-principles statistical mechanics approaches. The linkages between these distinct length scales are the thermodynamic potentials and the kinetic coefficients that emerge from first-principles statistical mechanics calculations and that then feed into the larger length scale phenomenological theories as materials specific parameters (right half of Figure 2). Mechanical properties also arise from phenomena that occur at many length scales. Unfortunately, phenomena that occur at different length scales often cannot be separated as distinctly as is possible with thermokinetic models. In this issue, Beyerlein et al. reviewReference Beyerlein, Xu, Llorca, El-Awady, Mianroodi and Svendsen51 the advances and the challenges that emerge in modeling mechanical properties within a multiscale framework.
Experiments and characterization
Experiments and characterization have long been at the heart of alloy design, critical for establishing the structure–property linkages. While tremendous strides have been made across a wide spectrum of instrumentation platforms, it is worth considering a few recent trends that specifically enhance alloy design, including improved resolution; in situ, three-dimensional (3D), and four-dimensional (4D) capabilities; model-driven characterization; and automation.
Resolution
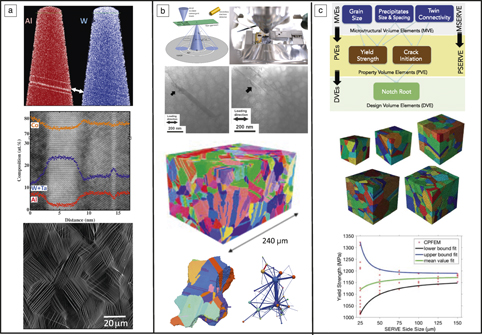
The ability to resolve structural and physical phenomena at all of the length scales and time scales relevant to alloy design is essential for the development of rigorous models for material behavior. With the advent of aberration-corrected transmission electron microscopy (TEM),Reference LeBeau, Findlay, Allen and Stemmer52,Reference Urban53 complementary metal oxide semiconductor (CMOS) direct electron detectors,Reference McMullan, Faruqi, Clare and Henderson54 high sensitivity energy-dispersive spectroscopy (EDS) with silicon drift x-ray detectors,Reference Scholssmacher, Klenov, Freitag and von Harrach55 and local electrode atom probe tomography,Reference McMullan, Faruqi, Clare and Henderson54 there is now an unprecedented ability to resolve structure and chemistry at the atomic scale. This has enabled, for example, rigorous studies of segregation to grain boundaries and stacking faults.Reference Titus, Mottura, Viswanathan, Suzuki, Mills and Pollock57–Reference Dingley, Meaden, Dingley and Day68 Refractory element segregation has been observed at superlattice intrinsic stacking faults in a new class of cobalt-based alloys containing L12 precipitates,Reference Titus, Mottura, Viswanathan, Suzuki, Mills and Pollock57,Reference Titus, Rhein, Wells, Dodge, Viswanathan, Mills, Van der Ven and Pollock58,Reference Pollock, Dibbern, Tsunekane, Zhu and Suzuki69,Reference Sato, Omori, Oikawa, Ohnuma, Kainuma and Ishida70 and is revealed by both local electrode atom probe tomography and high-angle annular dark field-scanning transmission electron microscopy (HAADF-STEM) (see Figure 3a). This provides a new pathway for control of fault energies and higher length scale mechanical properties sensitive to this property. Similar phenomena have also been observed in commercial nickel-based superalloys,Reference Viswanathan, Shi, Gene, Voronstov, Kovarik, Rae and Mills59,Reference Barba, Smith, Miao, Mills and Reed60 suggesting new strategies for alloying in both classes of materials. This approach to tailoring of interface properties promises improved fracture properties, control of grain growth, and stabilization of nanocrystalline structures.Reference Raabe, Herbig, Sandlobes, Li, Tytko, Kuzmina, Ponge and Choi61–Reference Dingley, Meaden, Dingley and Day68

Figure 3. Emerging capabilities for characterization of structure and properties. (a) High-resolution measurements of segregation at stacking faults in Co-based alloys detected by local electrode atom probe tomography (upper panel), high-angle annular dark field-scanning transmission electron microscopy (HAADF-STEM) in the TEM (middle panel), and Heaviside digital image correlation measurements (bottom panel) of strain localization at the grain scale in a Ti alloy. (b) Dynamic imaging of dislocation motion within a SEM using in situ straining with a microelectromechanical systems stage and a STEM detector (upper panel), mesoscale 3D data sets generated by TriBeam tomography, along with a network analysis of twin-related grains created by recrystallization (bottom panel). (c) Representative volume elements and property prediction by crystal plasticity finite element modeling (CPFEM) with prescribed degrees of confidence.Reference Kelly and Miller56,Reference Browning, Bonds, Campbell, Evans, LaGrange, Jungjohann, Masiel, McKeown, Mehraeen, Reed and Santala80,Reference Stinville, Lenthe, Echlin, Callahan, Texier and Pollock95,Reference Pinz, Weber, Lenthe, Uchic, Pollock and Ghosh96
At higher length scales, recent improvements in electron backscatter diffraction (EBSD) cameras and forward modeling of EBSD pattern formation enables rapid acquisition of high spatial resolution crystallographic information as well as quantification of geometrically necessary dislocation densities over large areas (mm2–cm2).Reference Wilkinson, Meaden and Dingley71,Reference Callahan and De Graef72 Combined with in situ straining and SEM-based digital image correlation (DIC),Reference Kammers and Daly73,Reference Stinville, Echlin, Callahan, Miller, Texier, Bridier, Bocher and Pollock74 including recent Heaviside function-based DIC analysis,Reference Bourdin, Stinville, Echlin, Callahan, Lenthe, Torbet, Texier, Bridier, Cormier, Villechaise, Pollock and Valle75 individual slip planes can be resolved and slip systems identified without the need for transmission electron microscopy (see Figure 3a, bottom). Other imaging modalities such as spatially resolved acoustic spectroscopyReference Smith, Li, Coulson, Clark, Somekh and Sharples76,Reference Mark, Li, Sharples and Withers77 provide previously unattainable resolution over large scan areas (>cm2). Given that structure exists across a wide variety of length scales, continued improvements in resolution are needed for all types of characterization signals, including electrons, x-rays, neutrons, light optical, and acoustic.
In situ, 3D, and 4D microscopy
Ideally, PSP relationships reflect the physics of the underlying processes that occur during processing and application of materials. In many cases, property prediction requires detailed knowledge of material structure and stress distribution in 3D and its evolution with time (4D). New suites of tomography and in situ tools that reveal processing kinetics and the dynamics of deformation are providing such insights. Emerging and rapidly maturing approaches include electron tomography,Reference Sharp, Barnard, Kaneko, Higashida and Midgley78,Reference Jornsanoh, Thollet, Ferreira, Masenelli-Varlot, Gauthier and Bogner79 dynamic transmission electron microscopy (DTEM),Reference Browning, Bonds, Campbell, Evans, LaGrange, Jungjohann, Masiel, McKeown, Mehraeen, Reed and Santala80 and in situ scanning transmission electron microscopy experiments in the SEM (STEM).Reference Browning, Bonds, Campbell, Evans, LaGrange, Jungjohann, Masiel, McKeown, Mehraeen, Reed and Santala80,Reference Callahan, Stinville, Yao, Echlin, De Graef, Gianola and Pollock81 Specialized microelectromechanical systems stages and improved focused ion beam (FIB) microscopes have enhanced the ability to fabricate small-scale samples to observe the dynamics of deformation. An example is shown in Figure 3b, where precipitate shearing and sequential fault creation/destruction events are captured in a STEM experiment.Reference Stinville, Yao, Callahan, Shin, Wang, Echlin, Pollock and Gianola82
Lab-scale x-ray tomography and ever-expanding synchrotron beamline facilities are revolutionizing our ability to collect 3D and 4D data.Reference Poulson, Nielsen, Lauridsen, Schmidt, Suter, Lienert, Margulies, Lorentzen and Juul Jensen83–Reference Oswald, Schuren, Pagan and Miller86 In cases where higher resolution information about chemistry or microstructure is required, automated serial sectioning systemsReference Uchic, Groeber, Dimiduk and Simmons87–Reference Spowart, Mullens and Puchala93 can now collect such information in reasonable periods of time (days to weeks). The 3D data set for a polycrystalline nickel-based superalloy (Figure 3b, center) was collected by the femtosecond laser-assisted TriBeam tomography approach in 132 h.Reference Lenthe, Stinville, Echlin and Pollock94–Reference Pinz, Weber, Lenthe, Uchic, Pollock and Ghosh96 The specific motivation for this data set was to extract 3D information on grain size and orientation and the connectivity of twin-related grains, shown in a network representation (Figure 3b, bottom) for prediction of strength and fatigue behavior.Reference Stinville, Lenthe, Echlin, Callahan, Texier and Pollock95–Reference Bagri, Weber, Stinville, Lenthe, Pollock, Woodward and Ghosh97
Model-driven characterization
With an increased focus on models for prediction of alloy properties, characterization will become more focused on supplying information to develop, parameterize, and validate models. For properties that are highly structure-sensitive, this is a major challenge, particularly if properties are to be predicted with a prescribed degree of confidence, which is important for component/device design. A primary consideration is obtaining structure information over a representative volume element. However, for metallic alloys, there is rarely a single representative volume element (RVE), and it may be necessary to consider several RVEs in connection with all critical microstructural featuresReference Bagri, Weber, Stinville, Lenthe, Pollock, Woodward and Ghosh97,Reference Echlin, Lenthe and Pollock98 (see Figure 3c). For the case of the 3D microstructure shown in Figure 3b, this includes grain size, precipitate size, and twin-related domain size. The volume required for full characterization of each of these features is referred to as a microstructural volume element (MVE). Since a property, such as yield strength, will likely depend on multiple microstructural features, the volume for convergence of the property, the property volume element (PVE), will have a different size than the individual MVE. Finally, the design volume element (DVE) will be prescribed by the region of interest in an engineering component; in this case, it is indicated as the volume of highly stressed material adjacent to a notch-like feature. If virtual microstructures are instantiated from distributions extracted from an experimental data set, then the statistically equivalent volume element for the microstructure is indicated as MSERVE and the property equivalent as PSERVE.
The 3D data sets can be meshed (Figure 3c, center) and used for property calculations in finite element models; the accompanying article in this issue by Beyerlein et al.Reference Beyerlein, Xu, Llorca, El-Awady, Mianroodi and Svendsen51 describes the associated challenges with development of constitutive models for mechanical behavior. For the polycrystalline nickel-based superalloy in Figure 3b–c, convergence to a yield strength of 1170 MPa occurs with 95% confidence at PVE size of 150 μm3.Reference Bagri, Weber, Stinville, Lenthe, Pollock, Woodward and Ghosh97 Properties such as fatigue crack initiation life converges at a higher volume element size of 500 μm3.Reference Lenthe, Stinville, Echlin and Pollock94,Reference Stinville, Lenthe, Echlin, Callahan, Texier and Pollock95 While this is only one example of the characterization capability developed to support modeling, future close coupling between models and characterization will dramatically improve predictive capabilities across a spectrum of properties.
Automation
To gather statistically significant quantities of data such as described in the previous section, automation of testing and characterization will become increasingly important. Combinatorial libraries, while they may sample large regions of compositional space, are not necessarily “high throughput,” since long lead times may be required, for example, to prepare the targets that develop the libraries. Characterization data of various modalities are often gathered with a high degree of individual intervention, control, and analysis. The article by Boyce and Uchic in this issueReference Boyce and Uchic99 highlights recent advances in automation, enabled by advances in robotics. Such automation inevitably leads to large volumes of data, addressed in the following section.
Materials data
A critically important piece of the PSP infrastructure is the data pillar (Figure 1). Materials data are complex, ranging from structured (tabular data in spreadsheets or databases), unstructured (images, video, instrument data), or semi-structured (i.e., extensible markup language [XML]). It is estimated that only about 5% of existing materials data are structured.Reference Gandomi and Haider100,Reference Jagadish101 With respect to structured materials data, crystallographic (Inorganic Crystal Structure Database [ICSD]), thermodynamic (CALPHAD) and emerging high-throughput databases described by van de Walle and AstaReference Sundman, Chen and Du10 in this issue are examples. Data are typically characterized by the five “Vs”: volume, variety, velocity, value, and veracity.Reference Kalidindi and De Graef7 Most materials data are not large in volume and are typically unstructured, making it difficult to capitalize on emerging artificial intelligence (AI)/machine-learning tools. However, some large companies with extensive historical material development databases do in some cases have sufficient data to take this approach; see the article by Suzuki et al. in this issue.Reference Suzuki, Shen and Kumar102
There are several notable exceptions where “big” materials data are generated. First, sensors that monitor processing operations are a source of data that are often collected, but typically, incompletely analyzed or leveraged to improve materials design. This is often the case due to the high volumes of information and lack of accompanying workflows to extract meaningful information from the data. Emerging 3D printing systems are an excellent example. For selective laser-melting systems, Spears and GoldReference Spears and Gold103 point out that for a laser scan rate of 100 mm/s and a part with geometric tolerances of +/–100 μm, a 50 kHz multichannel (laser power, photodiodes, IR signal, and position) data sampling rate is required for process monitoring at the scale of the melt pool. As a result, a three-day build will generate about 233 GB of data. With this volume of data, real-time data reduction is often required and visualization is a challenge, resulting in missed opportunities for the use of melt pool data to guide the development of alloys compatible with these new processes. This quickly narrows the field of alloys that are printed, since the process is iteratively optimized experimentally with great effort. As a result, only approximately 10 alloys are routinely printed currently, as compared to the approximately 5000 alloys available along conventional processing paths.Reference Martin, Yahata, Hundley, Mayer, Schadler and Pollock104 Systems that address the data challenge in 3D printing are under developmentReference Steed, Halsey, Dehoff, Yoder, Paquit and Powers105 and require close collaboration between interdisciplinary teams. Insights from this type of data promise to deliver critical information needed for development of a whole new suite of alloys that can be printed on demand. Extensions to other classes of processing also promises improvements in our ability to rapidly optimize new materials.
Tomography is another area of materials faced with a big data challenge. Serial sectioning data sets such as those shown in Figure 3b are 10–15 TB in size if raw EBSD patterns are saved (which is typically required for high-quality reconstruction). When multimodal information is collected (EBSD, EDS, and backscattered electrons [BSE]), there is an added complexity of merging data from different detectors with different distortions and resolutions. Many synchrotron beamlines generate on the orders of 1 TB/day of data; advanced detectors such as the GigaFRoST detector at the Swiss Light Source now generate 8.8 GB/s.Reference Wang, Steiner and Sepe106 The rate-limiting step is no longer acquisition of materials information, but reconstruction and analysis of that information. Collaborative efforts across beamline facilities are underway to deploy massively parallel codes and real-time algorithms.Reference Wang, De Carlo, Mancini, McNulty, Tieman, Bresnahan, Foster, Insley, Lane, von Laszewski, Kesselman, Su and Thiebaux107,Reference Gursoy, De Carlo, Xiao and Jacobsen108 Machine-learning algorithms are already proving useful for 3D reconstruction,Reference Charpagne, Strub and Pollock109 but nevertheless, the challenges of storing, transporting, sharing, and analyzing tomography data are still immense.
A recent study110 has considered the needs in terms of repositories, tools, and e-collaboration platforms for materials data and prioritized strategies in terms of potential impact and probability of success. While data efforts in materials are still in their infancy, it is clear that as the infrastructure matures to the point where AI and informatics tools can be applied across the PSP space,Reference Hill, Mulholland, Persson, Seshadri, Wolverton and Meredig111,Reference Dimiduk, Holm and Niezgoda112 the impact on alloy design will be profound.
Future needs
While the payoff for the discovery and rapid development of new alloys is high, there remain challenges and gaps. Specific areas that could have high impact include:
• The development of databases of first-principles finite temperature free-energy descriptions and diffusion coefficients that complement, augment, and are integrated with existing CALPHAD descriptions.
• New theoretical and computational tools with which to predict and rationalize nucleation events in the solid state.
• Advances in statistical mechanics methods that chart out rigorous links between thermodynamic and kinetic ingredients of phase-field models and the underlying electronic structure of materials.
• A larger suite of automated characterization and property measurement tools that generate experimental data across unexplored compositional spaces and accompanying data workflows for analysis.
• A materials data infrastructure that supports planning, acquisition, storage, analysis, and sharing of unstructured as well as large volumes of structured materials data.
• Development of materials-science-specific data science tools and greater interaction between the materials science and computer science communities for development of cross-disciplinary tools and training of students with skills in both domains.
• Improved theoretical understanding of materials behavior across the length scales and embodiment of this understanding in models and simulation tools that predict material properties, particularly those that are strongly influenced by rare features and events at the mesoscale.
Summary
We anticipate rapid progress in the next decade toward the goal of designing alloys “on demand” with properties that can be tailored to the needs of specific engineering systems. This article and accompanying articles in this issue highlight progress in theory, computation, data and advanced experimental techniques, applied across the length scales that support exploration and design across broad composition spaces. We hope these emerging approaches will motivate and inspire future innovations that further enhance and accelerate the discovery and design process.
Acknowledgments
The authors acknowledge the support of the National Science Foundation DMREF Grant No. DMR 1534264. T.M.P. also acknowledges a Vannevar Bush Faculty Fellowship, ONR Grant No. N00014–18–1-3031.

Tresa Pollock is the Alcoa Distinguished Professor of Materials at the University of California, Santa Barbara. She received her BS degree in metallurgical engineering from Purdue University and her PhD degree in materials science and engineering from the Massachusetts Institute of Technology. She was employed at General Electric Aircraft Engines from 1989 to 1991, conducting R&D on high-temperature alloys. Pollock was then a materials science and engineering faculty member at Carnegie Mellon University from 1991 to 1999 and the University of Michigan from 2000 to 2010. Her research focuses on the performance of materials in extreme environments, alloy design, and 3D materials characterization. She was elected to the US National Academy of Engineering in 2005, the German Academy of Sciences Leopoldina in 2015, and is a US Department of Defense Vannevar Bush Fellow, and Fellow of The Minerals, Metals & Materials Society and ASM International. Pollock can be reached by email at [email protected].

Anton Van der Ven is a professor of materials at the University of California, Santa Barbara. He studied metallurgy at the Katholieke Universiteit Leuven, Belgium, and obtained his PhD degree in materials science at the Massachusetts Institute of Technology. His research focuses on the links between the electronic structure of solids and their macroscopic properties using first-principles statistical mechanics, using a wide variety of materials classes for electrochemical energy storage and high-temperature aerospace applications. His research group develops statistical mechanics methods and accompanying software tools to predict the properties of complex crystals from first principles. Van der Ven can be reached by email at [email protected].