Introduction
The counterintuitive features of quantum mechanics such as superposition (“being at two places at the same time”) and entanglement (leading to “spooky action at a distance”) have been a subject of debate for much of the 20th century. After pioneering experiments with photonsReference Aspect, Grangier and Roger 1 showed that entanglement is indeed a part of nature, scientists began to wonder how these quantum resources could be put to use. A number of exciting opportunities have emerged: quantum computers, secure quantum communications, and quantum metrology.
Building a scalable quantum technology requires meeting two conflicting demands. On the one hand, a well-isolated system is desired that can be controlled with high precision. Arguably the best example is a single trapped atom. Indeed, many pioneering experiments on individual quantum systems were performed with single atoms;Reference Leibfried, Blatt, Monroe and Wineland 2 the 2012 Nobel Prize in Physics recognized the remarkable level of control achieved over neutral atoms and ions. On the other hand, the technology needs to be scalable. Solid-state systems have a clear advantage in this regard, offering the opportunity to adapt nanofabrication techniques developed in the semiconductor industry to build integrated quantum devices.Reference Hanson and Awschalom 3
Nitrogen-vacancy (NV) centers in diamond have emerged as one of the most promising candidates for implementing quantum technologies because they exhibit atom-like properties—long-lived spin quantum states and well-defined optical transitions—in a robust solid-state device (see the Introduction article in this issue). The NV center has spin degrees-of-freedom associated with both its bound electrons and nearby nuclear spins (see Figure 1 a–b), and, much like atomic states, these spins can be addressed using optical transitions (see Figure 1c). At the same time, the solid-state host allows for fast electrical and magnetic control using on-chip wiring and waveguides; similarly, photonic structures can be fabricated from the diamond crystal (see Figure 1d) to create an efficient optical interface (see the Loncar and Faraon, and Toyli et al. articles in this issue). In the past few years, a number of labs around the world have exploited this combination of atom-like properties and solid-state control to demonstrate a number of key functionalities required for quantum technologies. In this article, we describe a few of these experiments and discuss prospects and challenges for future applications.
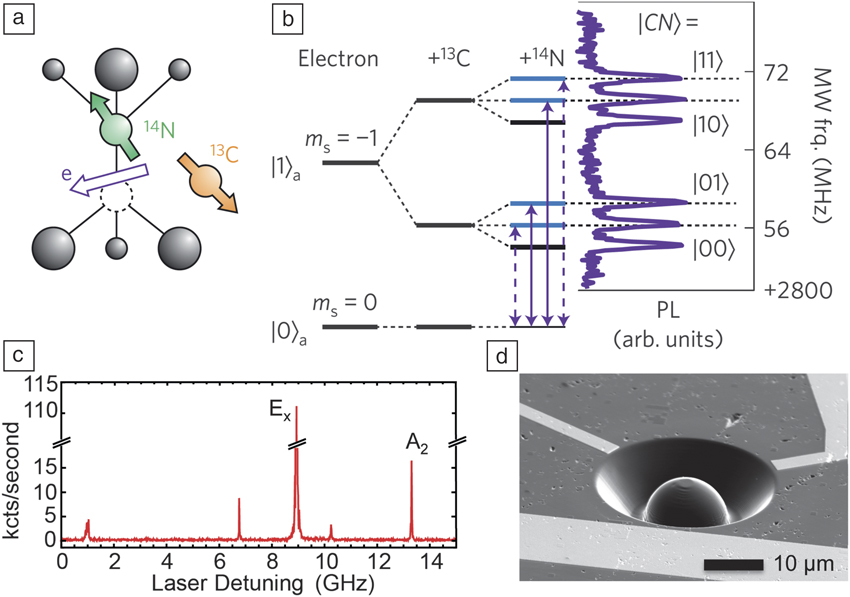
Figure 1. (a) The nitrogen-vacancy (NV) center structure, illustrating both the NV electronic spin and nuclear spins on the host nitrogen and nearby Reference Jelezko, Gaebel, Popa, Domhan, Gruber and Wrachtrup 13 C nuclei. Reprinted with permission from Reference 19. © 2012 Nature Publishing Group. (b) Energy levels associated with the NV electronic spin and two nuclear spin qubits (one 14 N, one 13 C). The S = 1 electronic spin has characteristic energy splittings in the GHz range. Hyperfine interactions shift its energy levels by ∼MHz for different nuclear spin states; this provides a mechanism for performing controlled logical operations by addressing specific transitions within this level scheme using resonant microwaves. PL, photoluminescence. Reprinted with permission from Reference Reference Pfaff, Taminiau, Robledo, Bernien, Markham, Twitchen and Hanson19. © 2012 Nature Publishing Group. (c) Resonant optical excitation (∼637 nm) of a NV center at low temperature (9 K). Scanning a laser in frequency while monitoring the NV fluorescence reveals narrow, spectrally resolved lines that correspond to transitions originating from specific electronic spin states. The sharpest lines are labeled by the symmetry of the excited state (Ex/A2) addressed by the resonant laser. Adapted from Reference 18. (d) Scanning electron microscope image of a solid immersion lens fabricated around a single NV center in diamond, with an integrated microwave strip line (front) and two electrodes (back) for controlling the defect quantum states. Adapted from Reference 18.
Controlling and reading single electron and nuclear spins
Much of the excitement about the NV center stems from its robust spin quantum states. In its ground state, the electrons bound to the NV center have a net spin S = 1, and superpositions of the spin sublevels (m s = –1, 0, 1) can exhibit coherent quantum evolution over long time scales. The typical sources of disturbance for spins in semiconductors and insulators—spin-orbit coupling and magnetic nuclei in the crystalline structure—are relatively weak for NV centers in diamond. For most diamond devices, spin coherence is limited by magnetic interactions with surrounding electronicReference Hanson, Dobrovitski, Feiguin, Gywat and Awschalom 4 and nuclear spins.Reference Childress, Gurudev Dutt, Taylor, Zibrov, Jelezko, Wrachtrup, Hemmer and Lukin 5 As a result, coherence times for the NV electronic spin range from a few microseconds in diamond with a significant amount of nitrogen impurities (the vast majority of diamonds fall in this category) to milliseconds in ultrapure isotopically purified diamonds.Reference Balasubramanian, Neumann, Twitchen, Markham, Kolesov, Mizuochi, Isoya, Achard, Beck, Tissler, Jacques, Hemmer, Jelezko and Wrachtrup 6
Remarkably, this coherence time is not a hard limit to the spin quantum state’s survival time. It was demonstrated in 2010 that by flipping the spin periodically, the disturbance from the surrounding spins could be nullifiedReference de Lange, Wang, Ristè, Dobrovitski and Hanson 7 – Reference Naydenov, Dolde, Hall, Shin, Fedder, Hollenberg, Jelezko and Wrachtrup 9 (see Figure 2 a–b). The essential idea is this: When the NV spin is being flipped, it experiences a reversed interaction with its environment. By flipping the NV spin sufficiently quickly, one can eliminate, on average, the effects of a slowly evolving environment. Ultimately, this so-called “dynamical decoupling” technique can extend the spin quantum coherence time to the spin-lattice relaxation time, removing effects of the surrounding electronic and nuclear spins. In ambient conditions, millisecond coherence times can thereby be achieved for NV spins even in natural isotopic samples,Reference Ryan, Hodges and Cory 8 , Reference van der Sar, Wang, Blok, Bernien, Taminiau, Toyli, Lidar, Awschalom, Hanson and Dobrovitski 10 and much longer times should be possible at cryogenic temperatures.Reference Takahashi, Hanson, van Tol, Sherwin and Awschalom 11

Figure 2. (a) Controlled rotations of a nitrogen-vacancy (NV) electronic spin at moderate (left) and high (right) microwave power. Fast spin control is critical for logical operations, and rapid spin flips can extend coherence times by averaging away effects of the environment. (b) Dynamical decoupling of the NV electronic spin. The “probability of the bright state” is a proxy for the remaining spin coherence; by increasing the number of spin flips (pulses) during a given time interval, the spin coherence can be significantly extended.Reference Ryan, Hodges and Cory 8 Reprinted with permission from Reference 8. © 2010 American Physical Society. (c) Free precession over time t, of a single Reference Jelezko, Gaebel, Popa, Domhan, Gruber and Wrachtrup 13 C nuclear spin in the vicinity of an optically illuminated NV center at room temperature. In these data, the y-axis is the probability of spin up. The measured coherence time is 0.5 ± 0.1s, and it can be extended to more than a second with dynamical decoupling techniques.Reference Maurer, Kucsko, Latta, Jiang, Yao, Bennett, Pastawski, Hunger, Chisholm, Markham, Twitchen, Cirac and Lukin 12 Reprinted with permission from Reference Reference Maurer, Kucsko, Latta, Jiang, Yao, Bennett, Pastawski, Hunger, Chisholm, Markham, Twitchen, Cirac and Lukin12. © 2012 AAAS.
Viewed from another perspective, however, the nearby spins can also be a resource. The magnetic interactions between the NV electronic spin and nearby nuclei (in particular the host nitrogen and 13 C isotopic impurities) allow NV-mediated access to individual nuclear spins that have extraordinarily long-lived quantum states. Even at room temperature, the coherence of these nuclear spins can persist for secondsReference Maurer, Kucsko, Latta, Jiang, Yao, Bennett, Pastawski, Hunger, Chisholm, Markham, Twitchen, Cirac and Lukin 12 (see Figure 2c), offering additional states for logical operations or a long-lived quantum memory.Reference Jelezko, Gaebel, Popa, Domhan, Gruber and Wrachtrup 13
These long coherence times stand in stark contrast to the fast time scales on which solid-state spins can be manipulated. Lithographically defined microwave waveguides can drive electronic spin transitions in nanoseconds (see Figure 2a),Reference de Lange, Wang, Ristè, Dobrovitski and Hanson 7 , Reference Fuchs, Dobrovitski, Toyli, Heremans and Awschalom 14 while nuclear spins can be rotated on microsecond time scales.Reference Jelezko, Gaebel, Popa, Domhan, Gruber and Wrachtrup 13 , Reference Dutt, Childress, Jiang, Togan, Maze, Jelezko, Zibrov, Hemmer and Lukin 15 Logical operations between quantum bits of information (qubits) stored in different spins can be achieved by selective excitation of specific transitions within the multi-spin energy levels (see Figure 1b). Intriguingly, it is even possible to combine two-spin logic gates with dynamical decoupling to preserve the coherence of a multi-spin system during logical operations.Reference van der Sar, Wang, Blok, Bernien, Taminiau, Toyli, Lidar, Awschalom, Hanson and Dobrovitski 10 Very recently, these ideas were applied to demonstrate an elementary quantum algorithm for fast searching—Grover’s algorithm—using two spins associated with a NV center,Reference van der Sar, Wang, Blok, Bernien, Taminiau, Toyli, Lidar, Awschalom, Hanson and Dobrovitski 10 hinting at the possibilities opened by the combination of long-lived coherence and fast control over spin states.
Arguably, these properties are not unique to the NV: In an appropriate host, many other types of spin qubits could exhibit similar coherence properties or achieve comparably fast control. The critical difference between the NV center and other solid-state spin systems lies in the optical properties of the NV defect. More than a decade ago, it was recognized that fluorescence from a single NV center could be used to observe transitions of its electronic spin, even at room temperature—a groundbreaking result at the time.Reference Gruber, Dräbenstedt, Tietz, Fleury, Wrachtrup and von Borczyskowski 16 In the past two years, this capability has been extended to the quantum regime: it is now possible to prepare the electronic and nuclear spins of a NV center with high fidelity and detect their quantum states in a single measurement.Reference Neumann, Beck, Steiner, Rempp, Fedder, Hemmer, Wrachtrup and Jelezko 17 , Reference Robledo, Childress, Bernien, Hensen, Alkemade and Hanson 18
Single shot spin readout is a critical capability for establishing the NV center as a viable qubit candidate. At cryogenic temperatures, phonon processes are suppressed, revealing the spectrally sharp optical transitions of the NV center (see Figure 1c). Reminiscent of hyperfine-resolved lines in atoms, these spin-dependent transitions create an exciting opportunity to adapt techniques pioneered in quantum optics and atomic physics to this solid-state defect. In particular, resonant optical pumping can initialize the electronic spin states with better than 99% fidelity, and resonance fluorescence can be exploited to directly detect the electronic spin state of the NV center.Reference Robledo, Childress, Bernien, Hensen, Alkemade and Hanson 18 By combining resonance fluorescence with integrated solid immersion lenses (see Figure 1d), a readout fidelity in excess of 95% has now been achieved (see Figure 3 a). Moreover, this measurement can be extended to nearby nuclear spins (achieved by mapping the nuclear spin state onto the electronic spin for readout), enabling single shot detection of a multiple-quantum-bit register.Reference Robledo, Childress, Bernien, Hensen, Alkemade and Hanson 18 , Reference Pfaff, Taminiau, Robledo, Bernien, Markham, Twitchen and Hanson 19
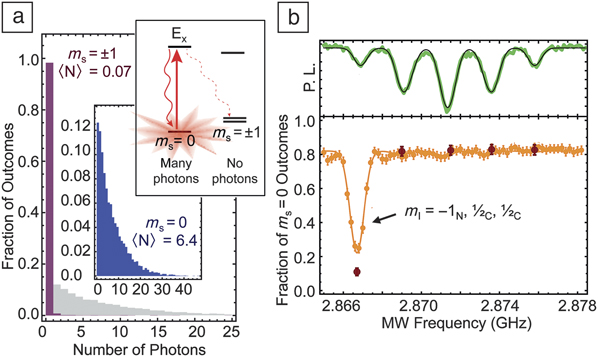
Figure 3. (a) Single-shot readout of the nitrogen-vacancy (NV) electronic spin by resonant excitation. Upper right: a laser resonant with a transition from the m s = 0 ground state to the Ex excited state (see Figure 1c) should yield fluorescence when the spin is in m s = 0; the NV will remain dark if the spin is in m s = ±1. The main figure shows a histogram of the number of photons detected from a single resonant laser pulse after optically pumping the NV into m s = ±1 (purple, 0.07 photons on average) or m s = 0 (blue, 6.4 photons on average).Reference Robledo, Childress, Bernien, Hensen, Alkemade and Hanson 18 Reprinted with permission from Reference Reference Robledo, Childress, Bernien, Hensen, Alkemade and Hanson18. © 2011 Nature Publishing Group. (b) Preparation-by-measurement of three nuclear spins and one electronic spin. The upper image shows a set of partially overlapping hyperfine lines associated with the 12 possible nuclear spin configurations. By correlating the electronic spin with the quantum state of the nuclear spins, measuring the electronic spin (using the technique shown in (a)), and conditioning on a specific measurement outcome, the nuclear spins can be polarized into a single well-defined quantum state (lower graph).Reference Robledo, Childress, Bernien, Hensen, Alkemade and Hanson 18 Reprinted with permission from Reference Reference Robledo, Childress, Bernien, Hensen, Alkemade and Hanson18. © 2011 Nature Publishing Group.
If a nuclear spin readout mechanism does not destroy the states that it is interrogating (quantum physicists call this a “non-demolition” measurement), the readout can be used to prepare the nuclear spins in a well-defined state by selecting for a certain measurement outcome. The simplest example is the fully polarized state in which all nuclear spins are pointing the same way (see Figure 3b). For comparison, to achieve such a polarization thermally, a strong magnetic field of 10 Tesla and a temperature far below 1 mK would be required. A non-demolition readout can also be used to create highly nonclassical states by measuring a joint property of two or more nuclear spins. Last year, entanglement between two nuclear spins near a NV center was created by reading out their combined parity (parity is even or odd depending on whether the nuclear spins are pointing in the same or in opposite directions). By combining this entanglement with individual spin readout, researchers were able to violate Bell’s inequality (a manifestation of nonclassical correlations between entangled qubits).Reference Pfaff, Taminiau, Robledo, Bernien, Markham, Twitchen and Hanson 19 As the first violation of Bell’s inequality using solid-state spins, this result demonstrates that experiments with NV centers have become sufficiently precise and sensitive to probe truly quantum phenomena.
Scalable connections
The electronic and nuclear spins associated with a single NV center form a highly coherent and controllable quantum register. They can be prepared, manipulated, and detected with high fidelity, and the field is ripe for exploration of quantum sensing devices or demonstration of elementary quantum algorithms with a small number of qubits. For long-term applications in quantum information science, however, it will be necessary to move beyond the handful of qubits attainable around a single NV defect and develop a scalable mechanism for coherently linking a network of NV-based registers.
One approach is based on magnetic interactions. Dipolar coupling of electronic spins could mediate interactions between nuclear spins associated with different NV centers,Reference Bermudez, Jelezko, Plenio and Retzker 20 offering a potentially scalable platform for information processing.Reference Yao, Jiang, Gorshkov, Maurer, Giedke, Cirac and Lukin 21 The electronic spins of NV centers separated by approximately 10 nm can exhibit coherent magnetic dipole-dipole interactions; initial experiments have observed a coupling strength of 43 kHz,Reference Neumann, Kolesov, Naydenov, Beck, Rempp, Steiner, Jacques, Balasubramanian, Markham, Twitchen, Pezzagna, Meijer, Twamley, Jelezko and Wrachtrup 22 well in excess of achievable spin decoherence rates, and these interactions have very recently been used to demonstrate entangling operations between two nearby NV center spins.Reference Dolde, Jakobi, Naydenov, Zhao, Pezzagna, Trautmann, Meijer, Neumann, Jelezko and Wrachtrup 29 Excitingly, a device based on such magnetic interactions could feasibly function at room temperature in ambient conditions.
Optical channels provide an alternate platform that is well suited to mediating interactions over macroscopic distances or in highly connected networks. At low temperatures, the spin-dependent optical transitions of a NV center (e.g., Figure 1c) provide a mechanism for entangling its electronic spin with an outgoing photon. If two NV centers’ electronic spins are each entangled with an outgoing photon, and the two photons can coherently interfere with each other on a beam splitter, then photon detection can project the NV spins onto an entangled state (see Figure 4 a).Reference Moehring, Maunz, Olmschenk, Younge, Matsukevich, Duan and Monroe 23

Figure 4. (a) Schematic for generating entanglement between distant spins. Two photons, each entangled with a different spin, interfere on a beam splitter (top). Detection of a photon on each output port can thereby project the spins onto a long-distance entangled state (bottom). (b) Level scheme for spin-photon entanglement illustrating the atomic-like polarization selection rules for radiative decay from a specific nitrogen-vacancy (NV) excited state (A2) to the ground state spin levels |m s〉 = |1〉 and |–1〉. Both pathways occur simultaneously, leaving the spin and the outgoing photon in an entangled state. σ+ and σ– denote opposite rotations of the polarized photons. (c) Two photon quantum interference. For this experiment, photons from different NV centers impinge on a 50/50 beam splitter, and the number of coincidence counts is shown as a function of the time between detection events on the two output ports. When the photons are perpendicularly polarized (top), no interference occurs. For parallel polarizations (bottom), the pronounced suppression of coincidence counts near zero delay is a signature of a high contrast (approximately 60%) two-photon interference, and indicates that the photons show some degree of indistinguishability.Reference Bernien, Childress, Robledo, Markham, Twitchen and Hanson 25 Reprinted with permission from Reference Reference Bernien, Childress, Robledo, Markham, Twitchen and Hanson25. © 2012 American Physical Society. (d) Dynamic stabilization of NV optical transitions. The top panel shows resonant excitation of a NV center optical transition as a function of time. In both panels, green arrows indicate pulses of 532 nm light, which changes local electric fields and shifts the frequency of the optical transition. Using nearby electrodes to provide feedback on the transition frequency, the observed frequency drifts can be eliminated (lower panel).27 Reprinted with permission from Reference Reference Acosta, Santori, Faraon, Huang, Fu, Stacey, Simpson, Ganesan, Tomljenovic-Hanic, Greentree, Prawer and Beausoleil27. © 2012 American Physical Society.
The first essential component for such optical connections is spin-photon entanglement. Recent experiments took advantage of the atomic-like selection rules for the NV center to create entanglement between the electronic spin quantum state and the polarization of an outgoing photon. In particular, one excited state of the NV center (labeled A2) decays to the m s = ±1 spin sublevels via opposite circular polarization pathways (see Figure 4b). If a NV center excited to A2 emits a photon that does not interact with the lattice (i.e., in the so-called zero phonon line), the resulting joint state of the electronic spin and the photon should be fully entangled. By measuring correlations between the spin state and photon polarization, it was possible to demonstrate spin-photon entanglement for the first time with a solid-state device.Reference Togan, Chu, Trifonov, Jiang, Maze, Childress, Dutt, Sorensen, Hemmer, Zibrov and Lukin 24
To generate entanglement between distant NV centers, the spins must each be entangled with photons that are otherwise indistinguishable and thus capable of coherently interfering on a beam splitter. In 2012, two groups observed the hallmark feature of such two-photon quantum interference: photon bunching.Reference Bernien, Childress, Robledo, Markham, Twitchen and Hanson 25 , Reference Sipahigil, Goldman, Togan, Chu, Markham, Twitchen, Zibrov, Kubanek and Lukin 26 Specifically, when two identical photons impinge on the input ports of a 50/50 beam splitter, they will always both emerge from the same output port. Experimentally, this is observed as a lack of simultaneous detection events (“coincidence counts”) on the two output ports (see Figure 4c). Such effects are challenging to discern with solid-state emitters. First, it is difficult to extract coherent photons with high efficiency from a high-index material. Worse, strain and fluctuating local electric fields change the frequency of emitted photons, making them spectrally distinguishable. Working with a solid-state device, however, can also provide a solution: Lithographically defined electrodes (see Figure 1d) can apply electric fields to shift the emission frequency (a DC Stark effect); it is even possible to stabilize spectral diffusion effects (see Figure 4d).Reference Acosta, Santori, Faraon, Huang, Fu, Stacey, Simpson, Ganesan, Tomljenovic-Hanic, Greentree, Prawer and Beausoleil 27 These initial demonstrations of spin-photon entanglement and two-photon quantum interference have laid the groundwork for generating entanglement between NV spins separated by macroscopic distances. Very recently, such remote NV-NV entanglement has been successfully achieved.Reference Bernien, Hensen, Pfaff, Koolstra, Blok, Robledo, Childress, Taminiau, Markham, Twitchen and Hanson 28 This experiment marks the beginning of a new era in quantum science in which entanglement between solid-state systems can be studied and exploited over human-scale distances.
Outlook
In the larger picture, several challenges remain before these exciting physics developments can be used in real-life technologies. Collection efficiencies for coherent photons need to be substantially improved by using cavities and optical nanostructures (see the Loncar and Faraon article in this issue). To create a quantum network, it will be necessary to generate entanglement while maintaining a coherent nuclear spin quantum memory. Moreover, fabrication techniques for deterministically creating NV centers with high spatial control are desired (see the Toyli et al. article in this issue). As the scientific community takes on these challenges, new devices and techniques will emerge, pushing forward applications and also enabling the exploration of new territory in physics.
Acknowledgments
R.H. acknowledges support from the Dutch Organization for Fundamental Research on Matter (FOM), the European Research Council through a Starting Grant, and the EU SOLID and DIAMANT programs.







