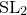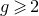1. Introduction
1.1 Quasimaps
Let
![]() $M({\mathsf{d}})$
be a moduli space of semistable Higgs
$M({\mathsf{d}})$
be a moduli space of semistable Higgs
![]() ${\rm{S}}{{\rm{L}}_2}$
-bundles of degree
${\rm{S}}{{\rm{L}}_2}$
-bundles of degree
![]() $\mathsf{d}$
on a curve
$\mathsf{d}$
on a curve
![]() $C$
of genus
$C$
of genus
![]() $g \geqslant 2$
. In this work, we consider quasimaps from a fixed elliptic curve
$g \geqslant 2$
. In this work, we consider quasimaps from a fixed elliptic curve
![]() $E$
to
$E$
to
![]() $M(\mathsf{d})$
. These are maps from
$M(\mathsf{d})$
. These are maps from
![]() $E$
to the stack of all Higgs sheaves mapping generically to
$E$
to the stack of all Higgs sheaves mapping generically to
![]() $M(\mathsf{d})$
.
$M(\mathsf{d})$
.
The (reduced) expected dimension of a moduli space of quasimaps up to translations by
![]() $E$
is 0, hence by [Reference NesterovNes23], it produces an invariant
$E$
is 0, hence by [Reference NesterovNes23], it produces an invariant
where
![]() ${{\mathsf{w}}} \in \mathbb{Z}$
is the degree of quasimaps. The Picard rank of
${{\mathsf{w}}} \in \mathbb{Z}$
is the degree of quasimaps. The Picard rank of
![]() $M(\mathsf{d})$
is 1, and the degree is taken with respect to the ample generator of
$M(\mathsf{d})$
is 1, and the degree is taken with respect to the ample generator of
![]() ${\rm{Pic}}({M(\mathsf{d})})$
. Assuming
${\rm{Pic}}({M(\mathsf{d})})$
. Assuming
![]() ${\mathsf{d}} = 1$
or, equivalently, that
${\mathsf{d}} = 1$
or, equivalently, that
![]() ${\mathsf{d}}$
is odd, we determine these invariants for odd degrees
${\mathsf{d}}$
is odd, we determine these invariants for odd degrees
![]() ${\mathsf{w}}$
. Let
${\mathsf{w}}$
. Let
 \begin{align*}{\mathsf{U}}(q):= \log \Bigg(\prod_{k\geqslant 0}(1-q^k)\Bigg).\end{align*}
\begin{align*}{\mathsf{U}}(q):= \log \Bigg(\prod_{k\geqslant 0}(1-q^k)\Bigg).\end{align*}
Theorem 1.1. We have
By [Reference NesterovNes23, Corollary 10.12], this also determines genus 1 Gromov–Witten invariant
![]() ${\mathsf{GW}}_{1,{\mathsf{w}}}^ \bullet $
of
${\mathsf{GW}}_{1,{\mathsf{w}}}^ \bullet $
of
![]() $M(1)$
since
$M(1)$
since
if
![]() ${\mathsf{w}}$
is odd. The invariant
${\mathsf{w}}$
is odd. The invariant
![]() ${\mathsf{GW}}_{1,{\mathsf{w}}}^ \bullet $
is defined analogously but via the moduli space of stable maps from
${\mathsf{GW}}_{1,{\mathsf{w}}}^ \bullet $
is defined analogously but via the moduli space of stable maps from
![]() $E$
. Moreover, by Corollary 3.7, these quasimap invariants determine certain Vafa–Witten invariants with insertions on the product
$E$
. Moreover, by Corollary 3.7, these quasimap invariants determine certain Vafa–Witten invariants with insertions on the product
![]() $C \times E$
.
$C \times E$
.
1.2 Degree 0 Higgs bundles
In [Reference NesterovNes23], a notion of extended degreeFootnote
1
![]() $\left( {{\mathsf{w}},{\mathsf{a}}} \right) \in \mathbb{Z} \oplus {\mathbb{Z}_2}$
of quasimaps to
$\left( {{\mathsf{w}},{\mathsf{a}}} \right) \in \mathbb{Z} \oplus {\mathbb{Z}_2}$
of quasimaps to
![]() $M(\mathsf{d})$
was defined (see Definition 2.5) as were the associated invariants for an arbitrary
$M(\mathsf{d})$
was defined (see Definition 2.5) as were the associated invariants for an arbitrary
![]() ${\mathsf{d}}$
,
${\mathsf{d}}$
,
If
![]() ${\mathsf{d}} = 1$
, the extended degree is determined by the parity of
${\mathsf{d}} = 1$
, the extended degree is determined by the parity of
![]() ${\mathsf{w}};$
that is,
${\mathsf{w}};$
that is,
![]() $\left( {{\mathsf{w}},{\mathsf{a}}} \right) = ({\mathsf{w}},\left[ {{\mathsf{w}}{]_2}} \right)$
, where
$\left( {{\mathsf{w}},{\mathsf{a}}} \right) = ({\mathsf{w}},\left[ {{\mathsf{w}}{]_2}} \right)$
, where
![]() ${[{{\mathsf{w}}}]_2}: = {{\mathsf{w}}}\ \mathrm{mod}\ 2.$
In particular, for odd
${[{{\mathsf{w}}}]_2}: = {{\mathsf{w}}}\ \mathrm{mod}\ 2.$
In particular, for odd
![]() ${{\mathsf{w}}}$
we have
${{\mathsf{w}}}$
we have
In this article, we also determine the quasimap invariants
![]() ${\mathsf{QM}}_{0,{{\mathsf{w}}}}^{1, \bullet }$
associated to a moduli space of degree 0 Higgs
${\mathsf{QM}}_{0,{{\mathsf{w}}}}^{1, \bullet }$
associated to a moduli space of degree 0 Higgs
![]() ${\rm{S}}{{\rm{L}}_2}$
-bundles
${\rm{S}}{{\rm{L}}_2}$
-bundles
![]() $M\!\left( 0 \right)$
.
$M\!\left( 0 \right)$
.
Theorem 1.2. We have
As it was argued in [Reference NesterovNes23], these invariants can be seen as Gromov–Witten–type invariants of the stack
![]() $M\!\left( 0 \right)$
. Moreover, we compute certain invariants for
$M\!\left( 0 \right)$
. Moreover, we compute certain invariants for
![]() ${{\mathsf{w}}} = 0$
in Corollary 3.9. Theorems 1.1 and 1.2, with Corollary 3.9, confirm parts of [Reference NesterovNes23, Conjecture A, B], thus providing evidence for [Reference NesterovNes23, Conjecture A, B, C].
${{\mathsf{w}}} = 0$
in Corollary 3.9. Theorems 1.1 and 1.2, with Corollary 3.9, confirm parts of [Reference NesterovNes23, Conjecture A, B], thus providing evidence for [Reference NesterovNes23, Conjecture A, B, C].
We want to draw the reader’s attention to a peculiar coincidence: Genus 1 positive-degree Gromov–Witten invariants of an elliptic curve
![]() $E$
are given by the following generating series:
$E$
are given by the following generating series:
 \begin{align*}-{\mathsf{U}}(q)=- \log\bigg( \prod_{k\geqslant 0}(1-q^k)\bigg),\end{align*}
\begin{align*}-{\mathsf{U}}(q)=- \log\bigg( \prod_{k\geqslant 0}(1-q^k)\bigg),\end{align*}
as is shown in [Reference DijkgraafDij95]. Our methods make this coincidence in some sense less surprising,Footnote
2
because in fact, the roles of
![]() $C$
and
$C$
and
![]() $E$
can be exchanged, allowing us to treat invariants
$E$
can be exchanged, allowing us to treat invariants
![]() ${\mathsf{QM}}_{{\mathsf{d}},{{\mathsf{w}}}}^{{\mathsf{a}}, \bullet }$
in terms of other invariants that are expressible via
${\mathsf{QM}}_{{\mathsf{d}},{{\mathsf{w}}}}^{{\mathsf{a}}, \bullet }$
in terms of other invariants that are expressible via
![]() $E$
alone. We now explain how this is done (see also Remark 4.15).
$E$
alone. We now explain how this is done (see also Remark 4.15).
1.3 Methods
The correspondence between quasimap invariants of
![]() $M(\mathsf{d})$
and Vafa–Witten invariants of
$M(\mathsf{d})$
and Vafa–Witten invariants of
![]() $C \times E$
, discussed in [Reference NesterovNes23], is essential. Our argument uses a combination of
$C \times E$
, discussed in [Reference NesterovNes23], is essential. Our argument uses a combination of
-
• wall-crossing for Vafa–Witten invariants and
-
• quasimap wall-crossing of [Reference NesterovNes21].
The wall-crossing for Vafa–Witten invariants is conjectured to be trivial for a complex surface
![]() $S$
with
$S$
with
![]() ${p_g}\!\left( S \right) \gt 0$
or, equivalently, with
${p_g}\!\left( S \right) \gt 0$
or, equivalently, with
![]() $b_2^ + \left( S \right) \gt 1$
. We will sketch an argument for its triviality by assembling various results from the existing literature. However, these results usually assume that
$b_2^ + \left( S \right) \gt 1$
. We will sketch an argument for its triviality by assembling various results from the existing literature. However, these results usually assume that
![]() ${b_1}\!\left( S \right) = 0$
, mainly in order to simplify the exposition. In our case,
${b_1}\!\left( S \right) = 0$
, mainly in order to simplify the exposition. In our case,
![]() $S$
is a product of two non-rational curves; hence,
$S$
is a product of two non-rational curves; hence,
![]() ${b_1}\!\left( S \right) \ne 0$
. We therefore make the assumption that existing results extend to the case of
${b_1}\!\left( S \right) \ne 0$
. We therefore make the assumption that existing results extend to the case of
![]() $S$
with
$S$
with
![]() ${b_1}\!\left( S \right) \ne 0$
. See Section 2.1 for more details.
${b_1}\!\left( S \right) \ne 0$
. See Section 2.1 for more details.
Changing stability on
![]() $C \times E$
from the one that has a high degree on
$C \times E$
from the one that has a high degree on
![]() $E$
to the one that has a high degree on
$E$
to the one that has a high degree on
![]() $C$
corresponds to passing from quasimaps
$C$
corresponds to passing from quasimaps
![]() $E \dashrightarrow M(\mathsf{d})$
to quasimaps
$E \dashrightarrow M(\mathsf{d})$
to quasimaps
![]() $C \dashrightarrow M^{\prime}( {\mathsf{a}})$
, where
$C \dashrightarrow M^{\prime}( {\mathsf{a}})$
, where
![]() $M^{\prime}( {\mathsf{a}})$
is a moduli space of Higgs
$M^{\prime}( {\mathsf{a}})$
is a moduli space of Higgs
![]() ${\rm{S}}{{\rm{L}}_2}$
-bundles on
${\rm{S}}{{\rm{L}}_2}$
-bundles on
![]() $E$
. Since the wall-crossing for Vafa–Witten invariants is trivial, this gives rise to an equivalence of associated invariants: Corollaries 2.12 and 3.7.
$E$
. Since the wall-crossing for Vafa–Witten invariants is trivial, this gives rise to an equivalence of associated invariants: Corollaries 2.12 and 3.7.
In this way, invariants
![]() ${\mathsf{QM}}_{{\mathsf{d}},{{\mathsf{w}}}}^{1, \bullet }$
correspond to quasimap invariants of
${\mathsf{QM}}_{{\mathsf{d}},{{\mathsf{w}}}}^{1, \bullet }$
correspond to quasimap invariants of
![]() $M^{\prime}(1)$
. This makes computation more accessible because
$M^{\prime}(1)$
. This makes computation more accessible because
![]() $M^{\prime}(1)$
is just a point, as there is a unique stable Higgs
$M^{\prime}(1)$
is just a point, as there is a unique stable Higgs
![]() ${\rm{S}}{{\rm{L}}_2}$
-bundle of degree 1 on
${\rm{S}}{{\rm{L}}_2}$
-bundle of degree 1 on
![]() $E$
. Hence, the corresponding quasimap invariants can be effectively computed by the quasimap wall-crossing: They will be equal to the wall-crossing invariants of the quasimap wall-crossing formula, which are just Euler characteristics of certain Quot schemes on
$E$
. Hence, the corresponding quasimap invariants can be effectively computed by the quasimap wall-crossing: They will be equal to the wall-crossing invariants of the quasimap wall-crossing formula, which are just Euler characteristics of certain Quot schemes on
![]() $E$
(which are quotiented by the action of
$E$
(which are quotiented by the action of
![]() $E$
). A summary of the preceding discussion is depicted in Figure 1.
$E$
). A summary of the preceding discussion is depicted in Figure 1.

Figure 1. Summary.
Complications arise due to the fact that in reality, one needs to consider quasisections of
![]() $C$
to
$C$
to
![]() $M^{\prime}( {\mathsf{a}})$
instead of quasimaps. This is a reason we did not put signs of equality in Figure 1 (another reason is that we have to find the quotient using
$M^{\prime}( {\mathsf{a}})$
instead of quasimaps. This is a reason we did not put signs of equality in Figure 1 (another reason is that we have to find the quotient using
![]() $E$
). Moduli spaces of quasisections and quasimaps are essentially isomorphic in this case, but the obstruction theories are not. This is the main source of technicalities in our calculations: The cosection of the obstruction theory of quasisections takes values in the canonical bundle of the curve
$E$
). Moduli spaces of quasisections and quasimaps are essentially isomorphic in this case, but the obstruction theories are not. This is the main source of technicalities in our calculations: The cosection of the obstruction theory of quasisections takes values in the canonical bundle of the curve
![]() $C$
, as is explained in Section 4.4. Nevertheless, we obtain the same vanishing results as in the case of an obstruction theory with a standard surjective cosection, Theorem 4.10. We refer to Section 2.3 for more on quasisections in our context. Quasisections are treated in greater detail for more general fibrations in [Reference Lee and WenLW23].
$C$
, as is explained in Section 4.4. Nevertheless, we obtain the same vanishing results as in the case of an obstruction theory with a standard surjective cosection, Theorem 4.10. We refer to Section 2.3 for more on quasisections in our context. Quasisections are treated in greater detail for more general fibrations in [Reference Lee and WenLW23].
1.4 Higher rank
Almost everything presented in this article applies to an arbitrary rank
![]() ${\mathsf{r}}$
, except for the following two results. Firstly, Claim 2.3 is stated for a prime rank
${\mathsf{r}}$
, except for the following two results. Firstly, Claim 2.3 is stated for a prime rank
![]() ${\mathsf{r}}$
because of Thomas’ vanishing result [Reference ThomasTho20, Corollary 5.30]. Secondly, the analysis of the wall-crossing Quot schemes in Section 5 is done only for
${\mathsf{r}}$
because of Thomas’ vanishing result [Reference ThomasTho20, Corollary 5.30]. Secondly, the analysis of the wall-crossing Quot schemes in Section 5 is done only for
![]() ${\mathsf{r}} = 2$
.
${\mathsf{r}} = 2$
.
The case of
![]() ${\mathsf{r}} \gt 2$
requires Quot schemes to parametrise quotients of higher rank on
${\mathsf{r}} \gt 2$
requires Quot schemes to parametrise quotients of higher rank on
![]() $E$
. One can always deform to a sum of line bundle and use torus-localisations. However, since a sum of line bundles is not stable and since we consider higher-rank quotients, the resulting Quot schemes have non-trivial obstruction theories. This slightly obscures localisation formulas; hence, it will be addressed elsewhere. To this end, we conjecture an expression for higher-rank invariants in Conjecture 4.17 and provide a basic check of the conjecture, Proposition 4.16.
$E$
. One can always deform to a sum of line bundle and use torus-localisations. However, since a sum of line bundles is not stable and since we consider higher-rank quotients, the resulting Quot schemes have non-trivial obstruction theories. This slightly obscures localisation formulas; hence, it will be addressed elsewhere. To this end, we conjecture an expression for higher-rank invariants in Conjecture 4.17 and provide a basic check of the conjecture, Proposition 4.16.
1.5 Even degrees
There is a good reason we cannot compute invariants for even degrees
![]() ${{\mathsf{w}}}$
(or, more generally, for degrees coprime to the rank) using the same methods. This case corresponds to the moduli space of degree 0 Higgs
${{\mathsf{w}}}$
(or, more generally, for degrees coprime to the rank) using the same methods. This case corresponds to the moduli space of degree 0 Higgs
![]() ${\rm{S}}{{\rm{L}}_2}$
-bundles
${\rm{S}}{{\rm{L}}_2}$
-bundles
![]() $M^{\prime}\!\left( 0 \right)$
on
$M^{\prime}\!\left( 0 \right)$
on
![]() $E$
. The space
$E$
. The space
![]() $M^{\prime}\!\left( 0 \right)$
is no longer a point. In fact, all Higgs bundles of degree 0 on
$M^{\prime}\!\left( 0 \right)$
is no longer a point. In fact, all Higgs bundles of degree 0 on
![]() $E$
are strictly semistable and are given by direct sums of degree 0 line bundles. As such, the moduli space
$E$
are strictly semistable and are given by direct sums of degree 0 line bundles. As such, the moduli space
![]() $M^{\prime}\!\left( 0 \right)$
is not complicated, but since it is a stack, its moduli spaces of quasimaps are not easily accessible.
$M^{\prime}\!\left( 0 \right)$
is not complicated, but since it is a stack, its moduli spaces of quasimaps are not easily accessible.
Quasimap invariants of even degrees are in some sense more appealing. For example, if
![]() ${{\mathsf{w}}} = 0$
, then the corresponding invariants give Euler characteristics of moduli spaces of Higgs bundles. If
${{\mathsf{w}}} = 0$
, then the corresponding invariants give Euler characteristics of moduli spaces of Higgs bundles. If
![]() ${{\mathsf{w}}} \gt 0$
, then by [Reference NesterovNes23, Section 7.2], they determine quasimap invariants of the gerbe given by the class
${{\mathsf{w}}} \gt 0$
, then by [Reference NesterovNes23, Section 7.2], they determine quasimap invariants of the gerbe given by the class
![]() $\alpha $
. Moreover,
$\alpha $
. Moreover,
![]() $K$
-theoretic invariants should give more refined topological invariants. In particular, one could potentially compute these topological invariants via the moduli space of degree 0 Higgs bundles on
$K$
-theoretic invariants should give more refined topological invariants. In particular, one could potentially compute these topological invariants via the moduli space of degree 0 Higgs bundles on
![]() $E$
by using Vafa–Witten wall-crossing, once quasimaps to moduli space of degree 0 Higgs bundles on
$E$
by using Vafa–Witten wall-crossing, once quasimaps to moduli space of degree 0 Higgs bundles on
![]() $E$
is better understood.
$E$
is better understood.
1.6 Notation and conventions
We denote the torus that scales Higgs fields by
![]() $\mathbb{C}_t^{\rm{*}},$
while the torus that scales
$\mathbb{C}_t^{\rm{*}},$
while the torus that scales
![]() ${\mathbb{P}^1}$
(with weight 1 at
${\mathbb{P}^1}$
(with weight 1 at
![]() $0 \in {\mathbb{P}^1}$
) by
$0 \in {\mathbb{P}^1}$
) by
![]() $\mathbb{C}_z^{\rm{*}}$
. We also denote
$\mathbb{C}_z^{\rm{*}}$
. We also denote
such that
![]() $t: = {e_{{\mathbb{C}_t}}}( {\bf{t}})$
and
$t: = {e_{{\mathbb{C}_t}}}( {\bf{t}})$
and
![]() $z: = {e_{{\mathbb{C}_z}}}( {\bf{z}})$
are the associated classes in the equivariant cohomology of a point.
$z: = {e_{{\mathbb{C}_z}}}( {\bf{z}})$
are the associated classes in the equivariant cohomology of a point.
Moduli spaces of Higgs sheaves are not proper; hence, we will always use the virtual localisation to define invariants. In order to make the notation less complicated, we denote
Finally, we will frequently use the fact that an obstruction theory of some space
![]() $M$
descends to the quotient
$M$
descends to the quotient
![]() $\left[ {M/G} \right]$
. That this is indeed true can be seen either by taking quotients in the category of derived stacks, since our group actions preserve the naturally defined derived enhancements, or by viewing the descent of an obstruction theory of
$\left[ {M/G} \right]$
. That this is indeed true can be seen either by taking quotients in the category of derived stacks, since our group actions preserve the naturally defined derived enhancements, or by viewing the descent of an obstruction theory of
![]() $M$
to
$M$
to
![]() $\left[ {M/G} \right]$
as an obstruction theory of
$\left[ {M/G} \right]$
as an obstruction theory of
![]() $\left[ {M/G} \right]$
relative to
$\left[ {M/G} \right]$
relative to
![]() $\left[ {{\rm{pt}}/G} \right]$
, which requires certain compatibility of the corresponding moduli problems, which also holds in our case.
$\left[ {{\rm{pt}}/G} \right]$
, which requires certain compatibility of the corresponding moduli problems, which also holds in our case.
2. Vafa–Witten and quasimap invariants
2.1 Preliminaries
Throughout the present article, we fix a rank
![]() ${\mathsf{r}}\geq 2$
. Only in the very end of Section 4 will we restrict to
${\mathsf{r}}\geq 2$
. Only in the very end of Section 4 will we restrict to
![]() ${\mathsf{r}} = 2$
. We need
${\mathsf{r}} = 2$
. We need
![]() ${\mathsf{r}} = 2$
for the analysis of Quot schemes in Section 5.
${\mathsf{r}} = 2$
for the analysis of Quot schemes in Section 5.
Let
![]() $C$
and
$C$
and
![]() $C^{\prime}$
be smooth, non-rational projective curves, and let
$C^{\prime}$
be smooth, non-rational projective curves, and let
be an ample
![]() $\mathbb{Q}$
-line bundle on the product
$\mathbb{Q}$
-line bundle on the product
![]() $C \times C^{\prime}$
. For the extremal values of
$C \times C^{\prime}$
. For the extremal values of
![]() $\delta $
, we introduce the following notation:
$\delta $
, we introduce the following notation:
Throughout this article, we will be using the identification
as provided by the Kunneth’s decomposition theorem. We define
to be a group of
![]() ${\mathsf{r}}$
-torsion lines bundles on
${\mathsf{r}}$
-torsion lines bundles on
![]() $C$
.
$C$
.
Definition 2.1. Let
![]() $\mathsf{d}$
and
$\mathsf{d}$
and
![]() $\mathsf{a}$
be integers such that
$\mathsf{a}$
be integers such that
![]() $0 \leqslant \mathsf{d},\mathsf{a} \lt \mathsf{r}$
. We define
$0 \leqslant \mathsf{d},\mathsf{a} \lt \mathsf{r}$
. We define
to be a moduli space of Higgs sheaves
![]() $\left( {F,\phi } \right),$
with a fixed determinant and traceless Higgs field
$\left( {F,\phi } \right),$
with a fixed determinant and traceless Higgs field
![]() $\phi \in \mathrm{Hom}\!\left( {F,F \otimes {\omega _{C \times C^{\prime}}}} \right)$
on
$\phi \in \mathrm{Hom}\!\left( {F,F \otimes {\omega _{C \times C^{\prime}}}} \right)$
on
![]() $C \times C^{\prime}$
, which are Gieseker-stable with respect to
$C \times C^{\prime}$
, which are Gieseker-stable with respect to
![]() ${L_\delta }$
. The class of
${L_\delta }$
. The class of
![]() $F$
is given as follows:
$F$
is given as follows:
 \begin{align*}{\rm{rk}}(F) & = {\mathsf{r}};\\{{\rm{c}}_1}(F) & = \left( {{\mathsf{d}},0,{\mathsf{a}}} \right);\\{\rm{\Delta }}(F) & : = {{\rm{c}}_1}{(F)^2} - 2{\mathsf{r}\rm{ch}}_2(F) = 2{{\mathsf{w}}}.\end{align*}
\begin{align*}{\rm{rk}}(F) & = {\mathsf{r}};\\{{\rm{c}}_1}(F) & = \left( {{\mathsf{d}},0,{\mathsf{a}}} \right);\\{\rm{\Delta }}(F) & : = {{\rm{c}}_1}{(F)^2} - 2{\mathsf{r}\rm{ch}}_2(F) = 2{{\mathsf{w}}}.\end{align*}
Throughout this article, we assume
which implies that there are no strictly semistable Higgs sheaves.
Remark 2.2. The assumption on the middle component of
![]() $c_1(F)$
being 0 is not restrictive because if
$c_1(F)$
being 0 is not restrictive because if
![]() $C$
and
$C$
and
![]() $C^{\prime}$
are chosen in the same way that, as the Jacobian of one curve is not an isogenous component of another, then
$C^{\prime}$
are chosen in the same way that, as the Jacobian of one curve is not an isogenous component of another, then
![]() ${H^1}(C) \otimes {H^1}\!\left( {C^{\prime}} \right)$
does not contain algebraic classes. The curves
${H^1}(C) \otimes {H^1}\!\left( {C^{\prime}} \right)$
does not contain algebraic classes. The curves
![]() $C^{\prime}$
and
$C^{\prime}$
and
![]() $C$
can always be deformed to such a setup. By the deformation invariance of Vafa–Witten invariants, we can therefore assume that the middle component is zero.
$C$
can always be deformed to such a setup. By the deformation invariance of Vafa–Witten invariants, we can therefore assume that the middle component is zero.
2.2 Vafa–Witten wall-crossing
Conjecturally, Vafa–Witten invariants are independent of stabilities for surfaces with
![]() ${p_g}\!\left( S \right) \gt 1$
. Let us present some evidences of this: By [Reference Manschot and MooreMM21], (physically derived) formulas for Vafa–Witten invariants for a surface
${p_g}\!\left( S \right) \gt 1$
. Let us present some evidences of this: By [Reference Manschot and MooreMM21], (physically derived) formulas for Vafa–Witten invariants for a surface
![]() $S$
with
$S$
with
![]() ${b_1}\!\left( S \right) = 0$
and
${b_1}\!\left( S \right) = 0$
and
![]() ${p_g}\!\left( S \right) \gt 1$
are independent of stabilities (see also the discussion in [Reference Tanaka and ThomasTT20, Section 1.6]). By [Reference Dijkgraaf, Park and SchroersDPS98], the same holds for Donaldson invariants for a surface with
${p_g}\!\left( S \right) \gt 1$
are independent of stabilities (see also the discussion in [Reference Tanaka and ThomasTT20, Section 1.6]). By [Reference Dijkgraaf, Park and SchroersDPS98], the same holds for Donaldson invariants for a surface with
![]() ${b_1}\!\left( S \right) \ne 0$
and
${b_1}\!\left( S \right) \ne 0$
and
![]() ${p_g}\!\left( S \right) \gt 1$
. It is therefore reasonable to expect that Vafa–Witten invariants (with even insertions) for a surface with
${p_g}\!\left( S \right) \gt 1$
. It is therefore reasonable to expect that Vafa–Witten invariants (with even insertions) for a surface with
![]() ${b_1}\!\left( S \right) \ne 0$
and
${b_1}\!\left( S \right) \ne 0$
and
![]() ${p_g}\!\left( S \right) \gt 1$
are also independent of stabilities. Products of non-rational curves are among such surfaces. We now derive a proof for this claim.
${p_g}\!\left( S \right) \gt 1$
are also independent of stabilities. Products of non-rational curves are among such surfaces. We now derive a proof for this claim.
Claim 2.3. Assume
![]() ${p_g}\!\left( S \right) \gt 0$
. If
${p_g}\!\left( S \right) \gt 0$
. If
![]() $\mathsf{r}$
is prime and there are no strictly semistable sheaves, then Vafa–Witten invariants with even
$\mathsf{r}$
is prime and there are no strictly semistable sheaves, then Vafa–Witten invariants with even
![]() $\mu $
-insertions are independent of stability.
$\mu $
-insertions are independent of stability.
Derivation of proof: Vafa–Witten invariants consist of instanton and monopole contributions. The instanton contributions are integrals on moduli spaces of stable sheaves on the surface (descendent Donaldson invariants). On the other hand, the monopole contributions are given by integrals on moduli spaces of flags of sheaves. See [Reference Tanaka and ThomasTT20] for more details.
The claim can therefore be proven by assembling the following results from the literature:
-
• Mochizuki’s universal expressions for descendent invariants on moduli spaces of sheaves on surfaces [Reference MochizukiMoc09]. To express instanton contributions via descendent invariants, we use Göttsche–Kool’s expressions of the virtual equivariant Euler class in terms of descendent invariants [Reference Cao and YauCY22];
-
• Thomas’ double-cosection argument, which shows that only vertical components contribute to the monopole branch [Reference ThomasTho20, Corollary 5.30];
-
• Laarakker’s expressions of vertical contributions in terms of integrals on nested Hilbert schemes [Reference LaarakkerLaa20, Theorem A] (see also [Reference Gholampour, Sheshmani and YauGSY20, Theorem 3] for the rank 2 case). Laarakker’s analysis extends to invariants with insertions.
It can be readily checked that Thomas’ and Laarakker’s results are independent of the assumption on
![]() ${b_1}\!\left( S \right)$
. On the other hand, Mochizuki’s result is more involved.
${b_1}\!\left( S \right)$
. On the other hand, Mochizuki’s result is more involved.
More conceptually, the independence of stability for Vafa–Witten invariants should be studied within the framework of Joyce’s wall-crossing [Reference JoyceJoy21].
Definition 2.4. Following [Reference Tanaka and ThomasTT20], we define Vafa–Witten invariants associated to a moduli space
![]() ${M^\delta }\!\left( {C \times C^{\prime},\mathsf{d},\mathsf{a},\mathsf{w}} \right)$
by the
${M^\delta }\!\left( {C \times C^{\prime},\mathsf{d},\mathsf{a},\mathsf{w}} \right)$
by the
![]() $\mathbb{C}_t^*$
-localisation,
$\mathbb{C}_t^*$
-localisation,
By Claim 2.3, they are independent of
![]() $\delta $
. For short, we will write
$\delta $
. For short, we will write
the same notation of which applies to all integrals that require
![]() $\mathbb{C}_t^{\rm{*}}$
-localisations.
$\mathbb{C}_t^{\rm{*}}$
-localisations.
2.3 Quasisection invariants
The importance of quasisections was already observed in [Reference OkounkovOko19, Section 7]. Here we apply them in the context of a relative moduli space of Higgs bundles.
Let
![]() ${K_{C \times C^{\prime}}}$
be the total space of the canonical bundle
${K_{C \times C^{\prime}}}$
be the total space of the canonical bundle
![]() ${\omega _{C \times C^{\prime}}}$
on
${\omega _{C \times C^{\prime}}}$
on
![]() $C \times C^{\prime}$
. The variety
$C \times C^{\prime}$
. The variety
![]() ${K_{C \times C^{\prime}}}$
admits projections both to
${K_{C \times C^{\prime}}}$
admits projections both to
![]() $C$
and to
$C$
and to
![]() $C^{\prime}$
:
$C^{\prime}$
:
We will consider various moduli spaces (that is, Quot schemes and moduli spaces of Higgs sheaves) relative to these projections.
Definition 2.5. We define
![]() $\mathfrak{M}_C^{\mathrm{rel}}( \mathsf{d}) \to C^{\prime}$
to be a relative moduli space of 1-dimensional compactly supported sheaves on
$\mathfrak{M}_C^{\mathrm{rel}}( \mathsf{d}) \to C^{\prime}$
to be a relative moduli space of 1-dimensional compactly supported sheaves on
![]() ${\pi _{C^{\prime}}}:{K_{C \times C^{\prime}}} \to C^{\prime}$
whose associated Higgs sheaves are of rank
${\pi _{C^{\prime}}}:{K_{C \times C^{\prime}}} \to C^{\prime}$
whose associated Higgs sheaves are of rank
![]() $\mathsf{r}$
, degree
$\mathsf{r}$
, degree
![]() $\mathsf{d}$
and with a fixed determinant and a traceless Higgs field. We refer to this moduli space as a relative moduli space of Higgs sheaves. By
$\mathsf{d}$
and with a fixed determinant and a traceless Higgs field. We refer to this moduli space as a relative moduli space of Higgs sheaves. By
![]() $M_C^{\mathrm{rel}}( \mathsf{d}) \to C^{\prime}$
, we denote its semistable locus.
$M_C^{\mathrm{rel}}( \mathsf{d}) \to C^{\prime}$
, we denote its semistable locus.
Let us denote
As in the absolute case, we have a determinant-line-bundle map
such that a class
![]() $u \in {H^{{\rm{ev}}}}\!\left( {C,\mathbb{Z}} \right)$
that satisfies
$u \in {H^{{\rm{ev}}}}\!\left( {C,\mathbb{Z}} \right)$
that satisfies
gives a trivilisation of the
![]() ${\mathbb{C}^{\rm{*}}}$
-gerbe
${\mathbb{C}^{\rm{*}}}$
-gerbe

or, in other words, a universal family on
![]() $\mathfrak{M}_{{\rm{rg}},C}^{{\rm{rel}}}(\mathsf{d})$
. For a class
$\mathfrak{M}_{{\rm{rg}},C}^{{\rm{rel}}}(\mathsf{d})$
. For a class
![]() $u \in {H^{{\rm{ev}}}}\!\left( {C,\mathbb{Z}} \right)$
such that
$u \in {H^{{\rm{ev}}}}\!\left( {C,\mathbb{Z}} \right)$
such that
![]() $\chi \!\left( {{\rm{v}} \cdot u} \right) = 0$
, the line bundle
$\chi \!\left( {{\rm{v}} \cdot u} \right) = 0$
, the line bundle
![]() $\lambda \!\left( u \right)$
descends to
$\lambda \!\left( u \right)$
descends to
![]() $\mathfrak{M}_{{\rm{rg}},C}^{{\rm{rel}}}(\mathsf{d})$
.
$\mathfrak{M}_{{\rm{rg}},C}^{{\rm{rel}}}(\mathsf{d})$
.
We define the theta line bundle
![]() ${\rm{\Theta }} \in {\rm{Pic}}\Big( {\mathfrak{M}_{{\rm{rg}},C}^{{\rm{rel}}}(\mathsf{d})} \Big)$
as follows:
${\rm{\Theta }} \in {\rm{Pic}}\Big( {\mathfrak{M}_{{\rm{rg}},C}^{{\rm{rel}}}(\mathsf{d})} \Big)$
as follows:
We also define the class of
![]() ${\rm{SL}}$
-trivialisations of the universal family of
${\rm{SL}}$
-trivialisations of the universal family of
![]() $\mathfrak{M}_C^{{\rm{rel}}}(\mathsf{d}):$
$\mathfrak{M}_C^{{\rm{rel}}}(\mathsf{d}):$
Equivalently,
![]() $\alpha $
is the Kunneth component of the first Chern class of the universal family modulo
$\alpha $
is the Kunneth component of the first Chern class of the universal family modulo
![]() ${\rm{r}}$
. The class
${\rm{r}}$
. The class
![]() $\alpha $
is the gerbe class of [Reference Hausel and ThaddeusHT03]. The classes
$\alpha $
is the gerbe class of [Reference Hausel and ThaddeusHT03]. The classes
![]() ${\rm{\Theta }}$
and
${\rm{\Theta }}$
and
![]() $\alpha $
will be used to define degrees of quasisections.
$\alpha $
will be used to define degrees of quasisections.
Remark 2.6. If gcd
![]() $( {\mathsf{r},\mathsf{d}})$
=1, then
$( {\mathsf{r},\mathsf{d}})$
=1, then
![]() $\alpha $
is a multiple of
$\alpha $
is a multiple of
![]() $\Theta $
modulo
$\Theta $
modulo
![]() $\mathsf{r}$
. However, this is not the case otherwise. It is useful to keep
$\mathsf{r}$
. However, this is not the case otherwise. It is useful to keep
![]() $\alpha $
for notational purposes, however, because even in the case when gcd
$\alpha $
for notational purposes, however, because even in the case when gcd
![]() $( {\mathsf{r},\mathsf{d}})$
=1, invariants behave very differently depending on the degree with respect to
$( {\mathsf{r},\mathsf{d}})$
=1, invariants behave very differently depending on the degree with respect to
![]() $\alpha $
.
$\alpha $
.
Definition 2.7. A quasisection of
![]() $M_C^{\mathrm{rel}}( \mathsf{d})$
is a section of the projection
$M_C^{\mathrm{rel}}( \mathsf{d})$
is a section of the projection
![]() ${p_{C^{\prime}}}:\mathfrak{M}_{rg,C}^{\mathrm{rel}}( \mathsf{d}) \to C^{\prime}$
,
${p_{C^{\prime}}}:\mathfrak{M}_{rg,C}^{\mathrm{rel}}( \mathsf{d}) \to C^{\prime}$
,
which maps generically to
![]() $M_C^{{\rm{rel}}}(\mathsf{d})$
. A quasisection is of degree
$M_C^{{\rm{rel}}}(\mathsf{d})$
. A quasisection is of degree
![]() $\left( {{{\mathsf{w}}},{\mathsf{a}}} \right) \in \mathbb{Z} \oplus {\mathbb{Z}_{\mathsf{r}}}: = \mathbb{Z} \oplus \mathbb{Z}/{\mathsf{r}}\mathbb{Z}$
, if
$\left( {{{\mathsf{w}}},{\mathsf{a}}} \right) \in \mathbb{Z} \oplus {\mathbb{Z}_{\mathsf{r}}}: = \mathbb{Z} \oplus \mathbb{Z}/{\mathsf{r}}\mathbb{Z}$
, if
We denote the moduli space of quasisections of
![]() $M_C^{{\rm{rel}}}(\mathsf{d})$
of degree
$M_C^{{\rm{rel}}}(\mathsf{d})$
of degree
![]() $\left( {{{\mathsf{w}}},{\mathsf{a}}} \right)$
by
$\left( {{{\mathsf{w}}},{\mathsf{a}}} \right)$
by
![]() $Q\!\left( {M_C^{{\rm{rel}}}(\mathsf{d}),{\mathsf{a}},{{\mathsf{w}}}} \right)$
.
$Q\!\left( {M_C^{{\rm{rel}}}(\mathsf{d}),{\mathsf{a}},{{\mathsf{w}}}} \right)$
.
The moduli spaces
![]() $Q\!\left( {M_C^{{\rm{rel}}}(\mathsf{d}),{\mathsf{a}},{{\mathsf{w}}}} \right)$
inherit
$Q\!\left( {M_C^{{\rm{rel}}}(\mathsf{d}),{\mathsf{a}},{{\mathsf{w}}}} \right)$
inherit
![]() $\mathbb{C}_t^{\rm{*}}$
-actions from
$\mathbb{C}_t^{\rm{*}}$
-actions from
![]() $\mathfrak{M}_C^{{\rm{rel}}}(\mathsf{d})$
. The properness of quasisections and the existence of a perfect obstruction theory is proven in the same way as in [Reference NesterovNes21, Reference NesterovNes23]; see also [Reference Lee and WenLW23].
$\mathfrak{M}_C^{{\rm{rel}}}(\mathsf{d})$
. The properness of quasisections and the existence of a perfect obstruction theory is proven in the same way as in [Reference NesterovNes21, Reference NesterovNes23]; see also [Reference Lee and WenLW23].
Definition 2.8. If
![]() $\mathrm{gcd}( {\mathsf{r},\mathsf{d}}) = 1$
, we define
$\mathrm{gcd}( {\mathsf{r},\mathsf{d}}) = 1$
, we define
to be quasisection invariants associated to a moduli space
![]() $Q\!\left( {M_C^{{\rm{rel}}}(\mathsf{d}),{\mathsf{a}},{{\mathsf{w}}}} \right)$
.
$Q\!\left( {M_C^{{\rm{rel}}}(\mathsf{d}),{\mathsf{a}},{{\mathsf{w}}}} \right)$
.
Note that by the definition of a relative moduli of sheaves, a section
is given by a sheaf on
Hence by [Reference NesterovNes23, Proposition 5.10], a moduli space of
![]() ${L_ + }$
-stable Higgs sheaves on
${L_ + }$
-stable Higgs sheaves on
![]() $C \times C^{\prime}$
is naturally a
$C \times C^{\prime}$
is naturally a
![]() ${{\rm{\Gamma }}_{C^{\prime}}}$
-torsor over the moduli space of quasisections of
${{\rm{\Gamma }}_{C^{\prime}}}$
-torsor over the moduli space of quasisections of
![]() $M_C^{{\rm{rel}}}(\mathsf{d})$
. On the other hand, the moduli space of
$M_C^{{\rm{rel}}}(\mathsf{d})$
. On the other hand, the moduli space of
![]() ${L_ - }$
-stable Higgs sheaves on
${L_ - }$
-stable Higgs sheaves on
![]() $C \times C^{\prime}$
is naturally a
$C \times C^{\prime}$
is naturally a
![]() ${{\rm{\Gamma }}_C}$
-torsor over the moduli space of quasisections of
${{\rm{\Gamma }}_C}$
-torsor over the moduli space of quasisections of
![]() $M_{C^{\prime}}^{{\rm{rel}}}(\mathsf{d})$
. Moreover, the corresponding obstruction theories match. This is summarised in the following proposition:
$M_{C^{\prime}}^{{\rm{rel}}}(\mathsf{d})$
. Moreover, the corresponding obstruction theories match. This is summarised in the following proposition:
Proposition 2.9.
If
![]() $\mathrm{gcd}( {\mathsf{r},\mathsf{d}}) = 1$
, we have
$\mathrm{gcd}( {\mathsf{r},\mathsf{d}}) = 1$
, we have
 \begin{align*}Q\Big( {M_{C^{\prime}}^{{\rm{rel}}}(\mathsf{d}),{\mathsf{a}},{{\mathsf{w}}}}\Big) & \cong \left[ {{{{M^ - }\!\left( {C \times C^{\prime},{\mathsf{d}},{\mathsf{a}},{{\mathsf{w}}}} \right)}}{{{{\rm{\Gamma }}_C}}}} \right]\\Q\Big( {M_C^{{\rm{rel}}}(\mathsf{d}),{\mathsf{a}},{{\mathsf{w}}}} \Big) & \cong \left[ {{M^ + }\!\left( {C \times C^{\prime},{\mathsf{d}},{\mathsf{a}},{{\mathsf{w}}}} \right)\!/{{\rm{\Gamma }}_{C^{\prime}}}} \right],\end{align*}
\begin{align*}Q\Big( {M_{C^{\prime}}^{{\rm{rel}}}(\mathsf{d}),{\mathsf{a}},{{\mathsf{w}}}}\Big) & \cong \left[ {{{{M^ - }\!\left( {C \times C^{\prime},{\mathsf{d}},{\mathsf{a}},{{\mathsf{w}}}} \right)}}{{{{\rm{\Gamma }}_C}}}} \right]\\Q\Big( {M_C^{{\rm{rel}}}(\mathsf{d}),{\mathsf{a}},{{\mathsf{w}}}} \Big) & \cong \left[ {{M^ + }\!\left( {C \times C^{\prime},{\mathsf{d}},{\mathsf{a}},{{\mathsf{w}}}} \right)\!/{{\rm{\Gamma }}_{C^{\prime}}}} \right],\end{align*}
such that the naturally defined obstruction theories on both sides match.
Proof. Similar to [Reference NesterovNes23, Proposition 5.10], see also [Reference Lee and WenLW23].
We use Proposition 2.9 as a justification for the following definition of invariants in the case of
![]() ${\rm{gcd}}({{\rm{r}},{\rm{d}}}) \ne 1:$
${\rm{gcd}}({{\rm{r}},{\rm{d}}}) \ne 1:$
Definition 2.10. If
![]() $\mathrm{gcd}( {\mathsf{r},\mathsf{d}}) \ne 1$
, we define
$\mathrm{gcd}( {\mathsf{r},\mathsf{d}}) \ne 1$
, we define
If
![]() ${\rm{gcd}}( {{\mathsf{r}},{\mathsf{a}}}) \ne 1$
, we define
${\rm{gcd}}( {{\mathsf{r}},{\mathsf{a}}}) \ne 1$
, we define
Remark 2.11. Proposition 2.9 implicitly depends on the choice of the universal family on the rigidified stack
![]() $\mathfrak{M}_{\mathrm{rg},C}^{\mathrm{rel}}$
. We return to this point in Section 3.2 for an elliptic curve.
$\mathfrak{M}_{\mathrm{rg},C}^{\mathrm{rel}}$
. We return to this point in Section 3.2 for an elliptic curve.
Using Claim 2.3 and Proposition 2.9, we obtain a curious correspondence between quasisection invariants of
![]() $M_C^{{\rm{rel}}}(\mathsf{d})$
and
$M_C^{{\rm{rel}}}(\mathsf{d})$
and
![]() $M_{C^{\prime}}^{{\rm{rel}}}( {\mathsf{a}})$
.
$M_{C^{\prime}}^{{\rm{rel}}}( {\mathsf{a}})$
.
Corollary 2.12.
If
![]() $\mathsf{r}$
is prime, we have
$\mathsf{r}$
is prime, we have
3. Genus 1 invariants
3.1 Group actions
For the rest of this article we assume that
![]() $C^{\prime}$
is an elliptic curve,
$C^{\prime}$
is an elliptic curve,
Since
![]() ${\pi _E}:{K_{C \times E}} \to E$
is a trivial fibration, the moduli space of quasisections to
${\pi _E}:{K_{C \times E}} \to E$
is a trivial fibration, the moduli space of quasisections to
![]() $M_C^{{\rm{rel}}}(\mathsf{d})$
is canonically isomorphic to a moduli space of quasimaps from
$M_C^{{\rm{rel}}}(\mathsf{d})$
is canonically isomorphic to a moduli space of quasimaps from
![]() $E$
to an absolute moduli space of Higgs bundles
$E$
to an absolute moduli space of Higgs bundles
![]() ${M_C}(\mathsf{d})$
on
${M_C}(\mathsf{d})$
on
![]() $C$
:
$C$
:
In fact, our primary interest is in quasimaps up to translations of
![]() $E$
; that is, in the quotient
$E$
; that is, in the quotient
where
![]() $E$
acts
$E$
acts
![]() ${\rm{on}}\;{Q_E}\!\left( {M(\mathsf{d}),{\mathsf{a}},{{\mathsf{w}}}} \right)$
by precomposition with a translation. A similar action exists on the level of moduli spaces
${\rm{on}}\;{Q_E}\!\left( {M(\mathsf{d}),{\mathsf{a}},{{\mathsf{w}}}} \right)$
by precomposition with a translation. A similar action exists on the level of moduli spaces
![]() ${M^\delta }\!\left( {C \times E,{\mathsf{d}},{\mathsf{a}},{{\mathsf{w}}}} \right)$
, which we now explain.
${M^\delta }\!\left( {C \times E,{\mathsf{d}},{\mathsf{a}},{{\mathsf{w}}}} \right)$
, which we now explain.
The group
naturally acts on sheaves. Here,
![]() $E$
acts by pulling back a sheaf with respect to a translation
$E$
acts by pulling back a sheaf with respect to a translation
![]() ${\tau _p}$
by a point
${\tau _p}$
by a point
![]() $p \in E$
, while
$p \in E$
, while
![]() ${\rm{Jac}}(E)$
acts by tensoring a sheaf with a line bundle
${\rm{Jac}}(E)$
acts by tensoring a sheaf with a line bundle
![]() $L$
. These operations commute. Overall,
$L$
. These operations commute. Overall,
Let
be the subgroup that fixes the determinant line bundle
![]() ${\mathcal{L}}$
of sheaves in a moduli space
${\mathcal{L}}$
of sheaves in a moduli space
![]() ${M^\delta }\!\left( {C \times E,{\mathsf{d}},{\mathsf{a}},{{\mathsf{w}}}} \right)$
. We define
${M^\delta }\!\left( {C \times E,{\mathsf{d}},{\mathsf{a}},{{\mathsf{w}}}} \right)$
. We define
The group
![]() ${{\rm{\Phi }}_{\mathsf{a}}}$
preserves rank
${{\rm{\Phi }}_{\mathsf{a}}}$
preserves rank
![]() ${\mathsf{r}}$
sheaves with determinant
${\mathsf{r}}$
sheaves with determinant
![]() ${\mathcal{L}}$
. The action of
${\mathcal{L}}$
. The action of
![]() ${{\rm{\Phi }}_{\mathsf{a}}}$
on sheaves therefore restricts to an action on
${{\rm{\Phi }}_{\mathsf{a}}}$
on sheaves therefore restricts to an action on
![]() ${M^\delta }\!\left( {C \times E,{\mathsf{d}},{\mathsf{a}},{{\mathsf{w}}}} \right)$
.
${M^\delta }\!\left( {C \times E,{\mathsf{d}},{\mathsf{a}},{{\mathsf{w}}}} \right)$
.
By our assumption on the classes in Definition 2.1, the line bundle
![]() ${\mathcal{L}}$
is of the form
${\mathcal{L}}$
is of the form
![]() $L \boxtimes L^{\prime}$
. Hence,
$L \boxtimes L^{\prime}$
. Hence,
![]() ${\rm{\Phi }}\!\left( {\mathcal{L}} \right)$
and therefore
${\rm{\Phi }}\!\left( {\mathcal{L}} \right)$
and therefore
![]() ${{\rm{\Phi }}_{\mathsf{a}}}$
depend only on the degree of
${{\rm{\Phi }}_{\mathsf{a}}}$
depend only on the degree of
![]() ${\mathsf{a}}$
. The group
${\mathsf{a}}$
. The group
![]() ${{\rm{\Phi }}_{\mathsf{a}}}$
also acts on
${{\rm{\Phi }}_{\mathsf{a}}}$
also acts on
![]() $\mathfrak{M}_E^{{\rm{rel}}}( {\mathsf{a}})$
. In the case of
$\mathfrak{M}_E^{{\rm{rel}}}( {\mathsf{a}})$
. In the case of
the action of
![]() ${{\rm{\Phi }}_{\mathsf{a}}}$
on
${{\rm{\Phi }}_{\mathsf{a}}}$
on
![]() $Q\!\left( {M_E^{{\rm{rel}}}( {\mathsf{a}}),{\mathsf{d}},{{\mathsf{w}}}} \right)$
can be seen as identification of maps by the automorphisms of the target. The importance of this action is due to the next two lemmas:
$Q\!\left( {M_E^{{\rm{rel}}}( {\mathsf{a}}),{\mathsf{d}},{{\mathsf{w}}}} \right)$
can be seen as identification of maps by the automorphisms of the target. The importance of this action is due to the next two lemmas:
Lemma 3.1. There is a canonical identification
such that the naturally defined obstruction theories on both sides match.
Proof. There exists a natural map
that is a
![]() ${{\rm{\Gamma }}_E}$
-torsor. There also exists a natural projection
${{\rm{\Gamma }}_E}$
-torsor. There also exists a natural projection
that is also a
![]() ${{\rm{\Gamma }}_E}$
-torsor. The map (3) is equivariant with respect to (4) and the corresponding actions of
${{\rm{\Gamma }}_E}$
-torsor. The map (3) is equivariant with respect to (4) and the corresponding actions of
![]() ${{\rm{\Phi }}_{\mathsf{a}}}$
and
${{\rm{\Phi }}_{\mathsf{a}}}$
and
![]() $E$
on the source and the target. It is not difficult to check that we obtain the desired identification after taking quotients. The rest follows from the same arguments as in [Reference NesterovNes23, Section 5.5].
$E$
on the source and the target. It is not difficult to check that we obtain the desired identification after taking quotients. The rest follows from the same arguments as in [Reference NesterovNes23, Section 5.5].
The action of
![]() ${{\rm{\Phi }}_{\mathsf{a}}}$
can be exchanged for an insertion. We are interested in
${{\rm{\Phi }}_{\mathsf{a}}}$
can be exchanged for an insertion. We are interested in
![]() $\mu $
-insertions, which are defined as follows:
$\mu $
-insertions, which are defined as follows:
 \begin{align*}\mu :{H^{\rm{*}}}\!\left( {C \times E,\mathbb{Q}} \right) & \to H_{{\mathbb{C}^{\rm{*}}}}^{{\rm{*}}}\left( {{M^\delta }\!\left( {C \times E,{\mathsf{d}},{\mathsf{a}},{{\mathsf{w}}}} \right),\mathbb{Q}} \right);\\\beta & \mapsto {\pi _{M{\rm{*}}}}\left( {{\rm{\Delta }}\!\left( {\mathcal{F}} \right)\!/2{\rm{r}} \cdot \pi _{X \times E}^{\rm{*}}\beta } \right),\end{align*}
\begin{align*}\mu :{H^{\rm{*}}}\!\left( {C \times E,\mathbb{Q}} \right) & \to H_{{\mathbb{C}^{\rm{*}}}}^{{\rm{*}}}\left( {{M^\delta }\!\left( {C \times E,{\mathsf{d}},{\mathsf{a}},{{\mathsf{w}}}} \right),\mathbb{Q}} \right);\\\beta & \mapsto {\pi _{M{\rm{*}}}}\left( {{\rm{\Delta }}\!\left( {\mathcal{F}} \right)\!/2{\rm{r}} \cdot \pi _{X \times E}^{\rm{*}}\beta } \right),\end{align*}
where
![]() ${\mathcal{F}}$
is the universal sheaf on
${\mathcal{F}}$
is the universal sheaf on
![]() ${M^\delta }\!\left( {C \times E,{\mathsf{d}},{\mathsf{a}},{{\mathsf{w}}}} \right)$
. Consider now the class
${M^\delta }\!\left( {C \times E,{\mathsf{d}},{\mathsf{a}},{{\mathsf{w}}}} \right)$
. Consider now the class
Lemma 3.2. We have
Proof. Similar to [Reference NesterovNes23, Proposition 5.26],
by Lemma 3.2 and Claim 2.3, invariants associated to a moduli space
![]() $\left[ {{M^\delta }\!\left( {C \times E,{\mathsf{d}},{\mathsf{a}},{{\mathsf{w}}}} \right)\!/{{\rm{\Phi }}_{\mathsf{a}}}} \right]$
are independent of
$\left[ {{M^\delta }\!\left( {C \times E,{\mathsf{d}},{\mathsf{a}},{{\mathsf{w}}}} \right)\!/{{\rm{\Phi }}_{\mathsf{a}}}} \right]$
are independent of
![]() $\delta $
.
$\delta $
.
Definition 3.3. If
![]() $\rm{gcd}( {\mathsf{r},\mathsf{d}}) = 1$
, we define
$\rm{gcd}( {\mathsf{r},\mathsf{d}}) = 1$
, we define
to be invariants associated with quotient moduli spaces
![]() $\left[ {{Q_E}\!\left( {M(\mathsf{d}),{\mathsf{a}},{{\mathsf{w}}}} \right)/E} \right]$
. If
$\left[ {{Q_E}\!\left( {M(\mathsf{d}),{\mathsf{a}},{{\mathsf{w}}}} \right)/E} \right]$
. If
![]() ${\rm{gcd}}\!\left( {{\mathsf{r}},{\mathsf{a}}} \right) = 1$
, we also define
${\rm{gcd}}\!\left( {{\mathsf{r}},{\mathsf{a}}} \right) = 1$
, we also define
to be invariants associated with the quotient moduli space
![]() $\left[ {Q\!\left( {M_E^{{\rm{rel}}}( {\mathsf{a}}),{\mathsf{d}},{{\mathsf{w}}}} \right)/{{\rm{\Phi }}_{\mathsf{a}}}} \right]$
.
$\left[ {Q\!\left( {M_E^{{\rm{rel}}}( {\mathsf{a}}),{\mathsf{d}},{{\mathsf{w}}}} \right)/{{\rm{\Phi }}_{\mathsf{a}}}} \right]$
.
We use Lemma 3.1 as a justification for the following definition of invariants in the case of
![]() ${\rm{gcd}}\!\left( {{\mathsf{r}},{\mathsf{d}}} \right) \ne 1$
and
${\rm{gcd}}\!\left( {{\mathsf{r}},{\mathsf{d}}} \right) \ne 1$
and
![]() ${\rm{gcd}}\!\left( {{\mathsf{r}},{\mathsf{a}}} \right)$
.
${\rm{gcd}}\!\left( {{\mathsf{r}},{\mathsf{a}}} \right)$
.
Definition 3.4. If
![]() $\rm{gcd}( {\mathsf{r},\mathsf{d}}) \ne 1$
, we define
$\rm{gcd}( {\mathsf{r},\mathsf{d}}) \ne 1$
, we define
If
![]() $\mathrm{gcd}\!\left( {{\mathsf{r}},{\mathsf{a}}} \right) \ne 1$
, we define
$\mathrm{gcd}\!\left( {{\mathsf{r}},{\mathsf{a}}} \right) \ne 1$
, we define
Remark 3.5. Note the presence of the equivariant parameter
![]() $t$
. This is due to the existence of
$t$
. This is due to the existence of
![]() $\mathbb{C}_t^*$
-equivariant cosections, which map to a line bundle of
$\mathbb{C}_t^*$
-equivariant cosections, which map to a line bundle of
![]() $\mathbb{C}_t^*$
-weight 1 and are constructed in [Reference NesterovNes23, Proposition 3.15]. We can divide by
$\mathbb{C}_t^*$
-weight 1 and are constructed in [Reference NesterovNes23, Proposition 3.15]. We can divide by
![]() $t$
, thereby obtaining
$t$
, thereby obtaining
![]() $\mathbb{Q}$
-valued invariants. This also corresponds to reducing the obstruction theory. However, the reduction of the obstruction theory is not necessary, as the cosection is equivariant and therefore does not lead to the vanishing of the virtual fundamental class; rather, it becomes a multiple of the equivariant parameter.
$\mathbb{Q}$
-valued invariants. This also corresponds to reducing the obstruction theory. However, the reduction of the obstruction theory is not necessary, as the cosection is equivariant and therefore does not lead to the vanishing of the virtual fundamental class; rather, it becomes a multiple of the equivariant parameter.
Remark 3.6. In the case of invariants up to translation by
![]() $E$
, the role of the
$E$
, the role of the
![]() $E$
-action is exchanged after passing from quasimaps of
$E$
-action is exchanged after passing from quasimaps of
![]() ${M_C}(\mathsf{d})$
to quasisections of
${M_C}(\mathsf{d})$
to quasisections of
![]() ${M_E}\!\left( \mathsf{a} \right)$
. For
${M_E}\!\left( \mathsf{a} \right)$
. For
![]() $\left[ {{Q_E}\!\left( {M(\mathsf{d}),\mathsf{a},\mathsf{w}} \right)/E} \right]$
, taking the quotient is an identification of maps by translations of the source curve
$\left[ {{Q_E}\!\left( {M(\mathsf{d}),\mathsf{a},\mathsf{w}} \right)/E} \right]$
, taking the quotient is an identification of maps by translations of the source curve
![]() $E$
. On the other hand, for
$E$
. On the other hand, for
![]() $\left[ {Q\!\left( {M_E^{\mathrm{rel}}(\mathsf{a}),\mathsf{d},\mathsf{w}} \right)\!/{\Phi _{\mathsf{a}}}} \right]$
, taking quotient can be seen as identification of quasisections by automorphisms of the target
$\left[ {Q\!\left( {M_E^{\mathrm{rel}}(\mathsf{a}),\mathsf{d},\mathsf{w}} \right)\!/{\Phi _{\mathsf{a}}}} \right]$
, taking quotient can be seen as identification of quasisections by automorphisms of the target
![]() $M_E^{\mathrm{rel}}(\mathsf{d})$
.
$M_E^{\mathrm{rel}}(\mathsf{d})$
.
Using Claim 2.3 and Lemma 3.2, we obtain the following result:
Corollary 3.7.
If
![]() $\mathsf{r}$
is prime, we have
$\mathsf{r}$
is prime, we have
Remark 3.8. Note that unlike in Corollary 2.12, we do not have the factor
![]() ${\mathsf{r}^{2g(E)}}$
on the left-hand side. This is because the group
${\mathsf{r}^{2g(E)}}$
on the left-hand side. This is because the group
![]() ${\Phi _{\mathsf{a}}}$
contains
${\Phi _{\mathsf{a}}}$
contains
![]() ${\Gamma _E}$
.
${\Gamma _E}$
.
3.2 Moduli spaces of Higgs sheaves and sheaves
From now on, we will assume that
![]() ${\rm{gcd}}\!\left( {{\mathsf{r}},{\mathsf{a}}} \right) = 1$
, unless stated otherwise. A moduli space of rank
${\rm{gcd}}\!\left( {{\mathsf{r}},{\mathsf{a}}} \right) = 1$
, unless stated otherwise. A moduli space of rank
![]() ${\mathsf{r}}$
and degree
${\mathsf{r}}$
and degree
![]() ${\mathsf{a}}$
stable Higgs
${\mathsf{a}}$
stable Higgs
![]() ${\rm{G}}{{\rm{L}}_{\rm{r}}}$
-bundles on
${\rm{G}}{{\rm{L}}_{\rm{r}}}$
-bundles on
![]() $E$
, denoted by
$E$
, denoted by
![]() $M_E^{{\rm{GL}}}( {\mathsf{a}})$
, is isomorphic to
$M_E^{{\rm{GL}}}( {\mathsf{a}})$
, is isomorphic to
![]() ${K_E}$
via the determinant-trace map,
${K_E}$
via the determinant-trace map,
Hence, a moduli space of stable Higgs sheaves on
![]() $E$
with a fixed determinant and a traceless Higgs field is a point,
$E$
with a fixed determinant and a traceless Higgs field is a point,
where
![]() $G$
is the unique stable sheaf with the given determinant. This is also holds relatively for the projection
$G$
is the unique stable sheaf with the given determinant. This is also holds relatively for the projection
![]() ${\pi _C}:{K_{C \times E}} \to C$
,
${\pi _C}:{K_{C \times E}} \to C$
,
Using Corollary 2.12, we obtain an immediate consequence for quasimaps of degree
![]() ${{\mathsf{w}}} = 0$
, which confirms a part of [Reference NesterovNes23, Conjecture B].
${{\mathsf{w}}} = 0$
, which confirms a part of [Reference NesterovNes23, Conjecture B].
Corollary 3.9.
If
![]() $\mathsf{r}$
is prime and
$\mathsf{r}$
is prime and
![]() $\mathsf{a} \ne 0$
, then
$\mathsf{a} \ne 0$
, then
Let us now consider quasimaps of degree
![]() $\;{{\mathsf{w}}} \ne 0$
. Since the unique Higgs sheaf in
$\;{{\mathsf{w}}} \ne 0$
. Since the unique Higgs sheaf in
![]() $M_E^{{\rm{rel}}}( {\mathsf{a}})$
has a zero Higgs field, a quasisection to
$M_E^{{\rm{rel}}}( {\mathsf{a}})$
has a zero Higgs field, a quasisection to
![]() $M_E^{{\rm{rel}}}( {\mathsf{a}})$
must factor through the moduli stack of Higgs sheaves with zero Higgs fields. The latter is just a moduli stack of sheaves on
$M_E^{{\rm{rel}}}( {\mathsf{a}})$
must factor through the moduli stack of Higgs sheaves with zero Higgs fields. The latter is just a moduli stack of sheaves on
![]() $E$
,
$E$
,
Since
![]() $\mathfrak{N}_E^{{\rm{rel}}}( {\mathsf{a}})$
is a relative moduli space of sheaves associated to a trivial fibration
$\mathfrak{N}_E^{{\rm{rel}}}( {\mathsf{a}})$
is a relative moduli space of sheaves associated to a trivial fibration
![]() $C \times E \to C$
, it trivialises canonically,
$C \times E \to C$
, it trivialises canonically,
The same applies for rigidified stacks.
The obstruction theory of
![]() $\mathfrak{M}_{{\rm{rg}},E}^{{\rm{rel}}}( {\mathsf{a}})$
is constructed as follows: Let
$\mathfrak{M}_{{\rm{rg}},E}^{{\rm{rel}}}( {\mathsf{a}})$
is constructed as follows: Let
be the universal
![]() $C$
-relative 1-dimensional sheaf and the canonical projection. The complex
$C$
-relative 1-dimensional sheaf and the canonical projection. The complex
![]() $R{\mathcal{H}}{om_\pi }\!\left( {{\mathcal{G}},{\mathcal{G}}} \right)$
descends to
$R{\mathcal{H}}{om_\pi }\!\left( {{\mathcal{G}},{\mathcal{G}}} \right)$
descends to
![]() $\mathfrak{M}_{{\rm{rg}},E}^{{\rm{rel}}}( {\mathsf{a}})$
. The obstruction theory for Higgs sheaves on a surface is constructed in [Reference Tanaka and ThomasTT20, Section 6], and the construction applies to Higgs sheaves on a curve. The spectral-curve construction identifies
$\mathfrak{M}_{{\rm{rg}},E}^{{\rm{rel}}}( {\mathsf{a}})$
. The obstruction theory for Higgs sheaves on a surface is constructed in [Reference Tanaka and ThomasTT20, Section 6], and the construction applies to Higgs sheaves on a curve. The spectral-curve construction identifies
![]() $C$
-relative 1-dimensional sheaves on
$C$
-relative 1-dimensional sheaves on
![]() ${K_{C \times E}}$
with
${K_{C \times E}}$
with
![]() $C$
-relative Higgs sheaves on
$C$
-relative Higgs sheaves on
![]() $C \times E$
with Higgs fields valued in
$C \times E$
with Higgs fields valued in
![]() ${\omega _{C \times E}}$
. Hence, the
${\omega _{C \times E}}$
. Hence, the
![]() $C$
-relative obstruction theory of
$C$
-relative obstruction theory of
![]() $\mathfrak{M}_{{\rm{rg}},E}^{{\rm{rel}}}( {\mathsf{a}})$
is given by the complex
$\mathfrak{M}_{{\rm{rg}},E}^{{\rm{rel}}}( {\mathsf{a}})$
is given by the complex
where
![]() $R{\mathcal{H}}o{m_\pi }{({\mathcal{G}},{\mathcal{G}})_0}$
is defined to be the cone
$R{\mathcal{H}}o{m_\pi }{({\mathcal{G}},{\mathcal{G}})_0}$
is defined to be the cone
Note that
![]() $\mathbb{T}_{\mathfrak{M}_{{\rm{rg}},E}^{{\rm{rel}}}( {\mathsf{a}})}^{{\rm{vir}}}$
does not restrict to the virtual tangent complex of the stack
$\mathbb{T}_{\mathfrak{M}_{{\rm{rg}},E}^{{\rm{rel}}}( {\mathsf{a}})}^{{\rm{vir}}}$
does not restrict to the virtual tangent complex of the stack
![]() $\mathfrak{N}_{{\rm{rg}},E}^{{\rm{rel}}}( {\mathsf{a}})$
.
$\mathfrak{N}_{{\rm{rg}},E}^{{\rm{rel}}}( {\mathsf{a}})$
.
3.3 Chern characters
For the purposes of wall-crossing, one needs to make a choice for a universal family on the rigidified stack
![]() $\mathfrak{M}_{{\rm{rg}},E}^{{\rm{rel}}}( {\mathsf{a}})$
. As explained in [Reference NesterovNes23, Section 3], this amounts to choosing
$\mathfrak{M}_{{\rm{rg}},E}^{{\rm{rel}}}( {\mathsf{a}})$
. As explained in [Reference NesterovNes23, Section 3], this amounts to choosing
![]() ${\mathsf{u}} \in {H^{{\rm{ev}}}}\!\left( {E,\mathbb{Z}} \right)$
such that
${\mathsf{u}} \in {H^{{\rm{ev}}}}\!\left( {E,\mathbb{Z}} \right)$
such that
![]() $\chi \!\left( {{\mathsf{u}} \cdot {\mathsf{v}}} \right) = 1.$
For a choice of such class
$\chi \!\left( {{\mathsf{u}} \cdot {\mathsf{v}}} \right) = 1.$
For a choice of such class
![]() ${\mathsf{u}} = \left( {{{\mathsf{u}}_1},{{\mathsf{u}}_2}} \right)$
, the sheaf
${\mathsf{u}} = \left( {{{\mathsf{u}}_1},{{\mathsf{u}}_2}} \right)$
, the sheaf
![]() $F$
on
$F$
on
![]() $C \times E$
associated to a quasisection
$C \times E$
associated to a quasisection
![]() $f:C \to \mathfrak{M}_{{\rm{rg}},E}^{{\rm{rel}}}( {\mathsf{a}})$
of degree
$f:C \to \mathfrak{M}_{{\rm{rg}},E}^{{\rm{rel}}}( {\mathsf{a}})$
of degree
![]() ${{\mathsf{w}}}$
has the following Chern character,
${{\mathsf{w}}}$
has the following Chern character,
where
![]() $\check{\mathsf{w}} $
is defined by the following system of equations:
$\check{\mathsf{w}} $
is defined by the following system of equations:
For example, if
![]() $( {{\mathsf{r}},{\mathsf{a}}}) = \left( {{\rm{r}},1} \right)$
, then
$( {{\mathsf{r}},{\mathsf{a}}}) = \left( {{\rm{r}},1} \right)$
, then
![]() ${\mathsf{u}} = \left( {1,0} \right)$
clearly satisfies
${\mathsf{u}} = \left( {1,0} \right)$
clearly satisfies
Using (7), we deduce that in this case,
4. Wall-crossing
4.1
 $\boldsymbol\epsilon $
-stable quasisections
$\boldsymbol\epsilon $
-stable quasisections
We will use Corollary 3.7 to compute genus 1 quasimap invariants of moduli spaces of Higgs bundles on
![]() $C$
. If
$C$
. If
![]() ${\rm{gcd}}( {{\mathsf{r}},{\mathsf{a}}}) = 1$
, then
${\rm{gcd}}( {{\mathsf{r}},{\mathsf{a}}}) = 1$
, then
hence, there are no sections of nonzero degree, and there is a unique section of degree zero. The quasimap wall-crossing for
![]() ${{\mathsf{w}}} \gt 0$
is therefore particularly simple here, as it gives equality of invariants associated to
${{\mathsf{w}}} \gt 0$
is therefore particularly simple here, as it gives equality of invariants associated to
![]() $\epsilon = {0^ + }$
and to the wall-crossing invariants. However, there are two complications:
$\epsilon = {0^ + }$
and to the wall-crossing invariants. However, there are two complications:
-
• the action of
 ${{\rm{\Phi }}_{\mathsf{a}}}$
on
${{\rm{\Phi }}_{\mathsf{a}}}$
on
 $\mathfrak{M}_E^{{\rm{rel}}}( {\mathsf{a}})$
and
$\mathfrak{M}_E^{{\rm{rel}}}( {\mathsf{a}})$
and -
•
 $C$
-relative setup,
$C$
-relative setup,
which obscure otherwise-simple computations.
Let us start with defining
![]() $\epsilon $
-stable quasisections. From now on, we simplify the notation in the following way:
$\epsilon $
-stable quasisections. From now on, we simplify the notation in the following way:
 \begin{align*}Q( {{\mathsf{a}},{{\mathsf{w}}}})& : = Q\left( {M_E^{{\rm{rel}}}( {\mathsf{a}}),{{\mathsf{w}}}} \right),\\Q{({\mathsf{a}},{{\mathsf{w}}})^ \bullet } & : = \left[ {{{Q\left( {M_E^{{\rm{rel}}}( {\mathsf{a}}),{{\mathsf{w}}}} \right)}}{{{{\rm{\Phi }}_{\mathsf{a}}}}}}\right];\end{align*}
\begin{align*}Q( {{\mathsf{a}},{{\mathsf{w}}}})& : = Q\left( {M_E^{{\rm{rel}}}( {\mathsf{a}}),{{\mathsf{w}}}} \right),\\Q{({\mathsf{a}},{{\mathsf{w}}})^ \bullet } & : = \left[ {{{Q\left( {M_E^{{\rm{rel}}}( {\mathsf{a}}),{{\mathsf{w}}}} \right)}}{{{{\rm{\Phi }}_{\mathsf{a}}}}}}\right];\end{align*}
the same applies to other related spaces.
Definition 4.1. A marked bubbling of
![]() $C$
is a pair
$C$
is a pair
![]() $\left( {C^{\prime},\mathbf{p},\iota } \right)$
, where
$\left( {C^{\prime},\mathbf{p},\iota } \right)$
, where
![]() $\left( {C^{\prime},\mathbf{p}} \right)$
is a connected, marked nodal curve of genus equal to
$\left( {C^{\prime},\mathbf{p}} \right)$
is a connected, marked nodal curve of genus equal to
![]() $g(C)$
and where
$g(C)$
and where
is a closed immersion. In other words,
![]() $C^{\prime}$
is an isotrivial, semistable degeneration of
$C^{\prime}$
is an isotrivial, semistable degeneration of
![]() $C$
.
$C$
.
Definition 4.2. Given
![]() $\epsilon \in {\mathbb{Q}_{ \gt 0}}$
, we define
$\epsilon \in {\mathbb{Q}_{ \gt 0}}$
, we define
![]() $Q_k^\epsilon ({\mathsf{a},\mathsf{w}})$
to be the moduli space of quasimaps of degree
$Q_k^\epsilon ({\mathsf{a},\mathsf{w}})$
to be the moduli space of quasimaps of degree
![]() $\mathsf{w}$
,
$\mathsf{w}$
,
such that
-
•
 ${f_{\mathfrak{N}( {\mathsf{a}})}}:\left( {C^{\prime},{\bf{p}}} \right) \to {\mathfrak{N}_{{\rm{rg}},E}}( {\mathsf{a}})$
is
${f_{\mathfrak{N}( {\mathsf{a}})}}:\left( {C^{\prime},{\bf{p}}} \right) \to {\mathfrak{N}_{{\rm{rg}},E}}( {\mathsf{a}})$
is
 $\epsilon $
-stable [Reference NesterovNes23, Definition 3.5];
$\epsilon $
-stable [Reference NesterovNes23, Definition 3.5]; -
•
 $\left( {C^{\prime},{\bf{p}}} \right)$
is a marked bubbling of
$\left( {C^{\prime},{\bf{p}}} \right)$
is a marked bubbling of
 $C$
with
$C$
with
 $k$
markings;
$k$
markings; -
•
 $\left[ {{f_C} \circ \iota :C \to C} \right] = {\rm{i}}{{\rm{d}}_C}$
.
$\left[ {{f_C} \circ \iota :C \to C} \right] = {\rm{i}}{{\rm{d}}_C}$
.
Since quasisections to
![]() $\mathfrak{M}_{{\rm{rg}},E}^{{\rm{rel}}}( {\mathsf{a}})$
factor through
$\mathfrak{M}_{{\rm{rg}},E}^{{\rm{rel}}}( {\mathsf{a}})$
factor through
![]() $\mathfrak{N}_{{\rm{rg}},E}^{{\rm{rel}}}( {\mathsf{a}})$
, a moduli space
$\mathfrak{N}_{{\rm{rg}},E}^{{\rm{rel}}}( {\mathsf{a}})$
, a moduli space
![]() $Q_k^\epsilon ( {{\mathsf{a}},{{\mathsf{w}}}})$
should be viewed as a moduli space of
$Q_k^\epsilon ( {{\mathsf{a}},{{\mathsf{w}}}})$
should be viewed as a moduli space of
![]() $\epsilon $
-stable quasisections to
$\epsilon $
-stable quasisections to
![]() $\mathfrak{M}_E^{{\rm{rel}}}( {\mathsf{a}})$
. The fact that these moduli spaces are proper follows from the arguments of [Reference NesterovNes21, Reference NesterovNes23]. Recall the embedding (5), which also holds for rigidified stacks,
$\mathfrak{M}_E^{{\rm{rel}}}( {\mathsf{a}})$
. The fact that these moduli spaces are proper follows from the arguments of [Reference NesterovNes21, Reference NesterovNes23]. Recall the embedding (5), which also holds for rigidified stacks,
we thus endow
![]() $Q_k^\epsilon ( {{\mathsf{a}},{{\mathsf{w}}}})$
with the obstruction theory given by the complex
$Q_k^\epsilon ( {{\mathsf{a}},{{\mathsf{w}}}})$
with the obstruction theory given by the complex
Its perfectness is proven in the same vein as in [Reference NesterovNes21, Reference NesterovNes23].
Let us indicate what moduli spaces
![]() $Q_k^\epsilon ( {{\mathsf{a}},{{\mathsf{w}}}})$
are for the extremal values of
$Q_k^\epsilon ( {{\mathsf{a}},{{\mathsf{w}}}})$
are for the extremal values of
![]() $\epsilon $
. Using the same notation as in (1), if
$\epsilon $
. Using the same notation as in (1), if
![]() $\epsilon = - $
, we get
$\epsilon = - $
, we get
If
![]() $\epsilon = + $
, then
$\epsilon = + $
, then
 \begin{align*}Q_0^ + ( {{\mathsf{a}},{{\mathsf{w}}}}) & = {\rm{pt\;\;\;\;if}}\ {\mathsf{w}} = 0;\\[4pt]Q_0^ + ( {{\mathsf{a}},{{\mathsf{w}}}}) & = \emptyset {\rm{\;\;\;\;\;\;\;if}}\ {\mathsf{w}} \ne 0.\end{align*}
\begin{align*}Q_0^ + ( {{\mathsf{a}},{{\mathsf{w}}}}) & = {\rm{pt\;\;\;\;if}}\ {\mathsf{w}} = 0;\\[4pt]Q_0^ + ( {{\mathsf{a}},{{\mathsf{w}}}}) & = \emptyset {\rm{\;\;\;\;\;\;\;if}}\ {\mathsf{w}} \ne 0.\end{align*}
We now discuss the wall-crossing between invariants associated to different values of
![]() $\epsilon $
.
$\epsilon $
.
Definition 4.3. Let
![]() $GQ({\mathsf{a},\mathsf{w}})$
be a moduli space of prestable quasimaps of degree
$GQ({\mathsf{a},\mathsf{w}})$
be a moduli space of prestable quasimaps of degree
![]() $\mathsf{w}$
,
$\mathsf{w}$
,
such that
![]() $\infty \in {\mathbb{P}^1}$
is mapped to the stable locus. Consider a
$\infty \in {\mathbb{P}^1}$
is mapped to the stable locus. Consider a
![]() $\mathbb{C}_z^{\rm{*}}$
-action on the source
$\mathbb{C}_z^{\rm{*}}$
-action on the source
![]() ${\mathbb{P}^1}$
with weight
${\mathbb{P}^1}$
with weight
![]() $1$
at
$1$
at
![]() $0 \in {\mathbb{P}^1}$
. It thus induces a
$0 \in {\mathbb{P}^1}$
. It thus induces a
![]() $\mathbb{C}_z^{\rm{*}}$
-action on
$\mathbb{C}_z^{\rm{*}}$
-action on
![]() $GQ( {{\mathsf{a}},{{\mathsf{w}}}})$
. We define
$GQ( {{\mathsf{a}},{{\mathsf{w}}}})$
. We define
to be the
![]() $\mathbb{C}_z^{\rm{*}}$
-fixed locus.
$\mathbb{C}_z^{\rm{*}}$
-fixed locus.
As in the case of
![]() $Q_k^\epsilon ( {{\mathsf{a}},{{\mathsf{w}}}})$
, we endow
$Q_k^\epsilon ( {{\mathsf{a}},{{\mathsf{w}}}})$
, we endow
![]() $GQ( {{\mathsf{a}},{{\mathsf{w}}}})$
with the obstruction theory given by the complex
$GQ( {{\mathsf{a}},{{\mathsf{w}}}})$
with the obstruction theory given by the complex
using the embedding
![]() $\mathfrak{N}_{{\rm{rg}},E}^{{\rm{rel}}}( {\mathsf{a}}) \hookrightarrow \mathfrak{M}_{{\rm{rg}},E}^{{\rm{rel}}}( {\mathsf{a}})$
. The space
$\mathfrak{N}_{{\rm{rg}},E}^{{\rm{rel}}}( {\mathsf{a}}) \hookrightarrow \mathfrak{M}_{{\rm{rg}},E}^{{\rm{rel}}}( {\mathsf{a}})$
. The space
![]() ${W^{{\rm{rel}}}}( {{\mathsf{a}},{{\mathsf{w}}}})$
inherits the obstruction theory defined by the fixed part of the obstruction theory of
${W^{{\rm{rel}}}}( {{\mathsf{a}},{{\mathsf{w}}}})$
inherits the obstruction theory defined by the fixed part of the obstruction theory of
![]() $GQ( {{\mathsf{a}},{{\mathsf{w}}}})$
, as well as the virtual normal bundle
$GQ( {{\mathsf{a}},{{\mathsf{w}}}})$
, as well as the virtual normal bundle
![]() ${N^{{\rm{vir}}}}$
defined by the moving part of the obstruction theory.
${N^{{\rm{vir}}}}$
defined by the moving part of the obstruction theory.
4.2 Moduli spaces of flags
As before, there exists a canonical identification of moduli spaces
where
![]() $W( {{\mathsf{a}},{{\mathsf{w}}}})$
is the analogous space defined via quasimaps to
$W( {{\mathsf{a}},{{\mathsf{w}}}})$
is the analogous space defined via quasimaps to
![]() ${\mathfrak{N}_E}( {\mathsf{a}})$
. By [Reference OberdieckObe21, Section 4], the space
${\mathfrak{N}_E}( {\mathsf{a}})$
. By [Reference OberdieckObe21, Section 4], the space
![]() $W( {{\mathsf{a}},{{\mathsf{w}}}})$
admits a description in terms of moduli spaces of flags, which we now recall. In what follows, by
$W( {{\mathsf{a}},{{\mathsf{w}}}})$
admits a description in terms of moduli spaces of flags, which we now recall. In what follows, by
![]() $G$
we denote the unique stable sheaf of degree
$G$
we denote the unique stable sheaf of degree
![]() ${\rm{a}}$
with a fixed determinant supported on the zero section in
${\rm{a}}$
with a fixed determinant supported on the zero section in
![]() ${K_E}$
. We also define
${K_E}$
. We also define
Let
be a moduli space of flags such that consecutive terms are allowed to be equal. To each
![]() ${F_ \bullet }$
and a choice of an integer
${F_ \bullet }$
and a choice of an integer
![]() $k \in \mathbb{Z}$
, we can associated a
$k \in \mathbb{Z}$
, we can associated a
![]() ${\mathbb{C}^{\rm{*}}}$
-equivariant, torsion-free sheaf
${\mathbb{C}^{\rm{*}}}$
-equivariant, torsion-free sheaf
![]() ${\mathcal{F}}$
on
${\mathcal{F}}$
on
![]() ${K_E} \times {\mathbb{A}^1}$
,
${K_E} \times {\mathbb{A}^1}$
,
In fact, for torsion-free sheaves
![]() $G$
, such association is an equivalence between
$G$
, such association is an equivalence between
![]() ${\mathbb{C}^{\rm{*}}}$
-fixed torsion-free sheaves on
${\mathbb{C}^{\rm{*}}}$
-fixed torsion-free sheaves on
![]() ${K_E} \times {\mathbb{A}^1}$
and weighted flags (up to a choice of
${K_E} \times {\mathbb{A}^1}$
and weighted flags (up to a choice of
![]() $k$
). Moreover, each
$k$
). Moreover, each
![]() ${\mathbb{C}^{\rm{*}}}$
-fixed sheaf in
${\mathbb{C}^{\rm{*}}}$
-fixed sheaf in
![]() $W( {{\mathsf{a}},{{\mathsf{w}}}})$
is canonically
$W( {{\mathsf{a}},{{\mathsf{w}}}})$
is canonically
![]() ${\mathbb{C}^{\rm{*}}}$
-equivariant. Let us denote by
${\mathbb{C}^{\rm{*}}}$
-equivariant. Let us denote by
the locus of flags that correspond to sheaves in
![]() $W( {{\mathsf{a}},{{\mathsf{w}}}})$
. By construction, we have
$W( {{\mathsf{a}},{{\mathsf{w}}}})$
. By construction, we have
Analogously, let
![]() ${\rm{F}}{{\rm{l}}^{{\rm{rel}}}}( {{\mathsf{a}},{{\mathsf{w}}}})$
be the relative moduli space of flags of
${\rm{F}}{{\rm{l}}^{{\rm{rel}}}}( {{\mathsf{a}},{{\mathsf{w}}}})$
be the relative moduli space of flags of
![]() ${(\pi _E^{\rm{*}}G)_{|C \times E}}$
on the relative surface
${(\pi _E^{\rm{*}}G)_{|C \times E}}$
on the relative surface
![]() ${\pi _C}:{K_{C \times E}} \to C$
. Viewing quotients of
${\pi _C}:{K_{C \times E}} \to C$
. Viewing quotients of
![]() $G$
as quotients of a sheaf on
$G$
as quotients of a sheaf on
![]() $E$
, on
$E$
, on
![]() ${K_E}$
or
${K_E}$
or
![]() $C$
-relatively on
$C$
-relatively on
![]() ${K_{C \times E}}$
is equivalent. Hence, identification (11) also holds relatively:
${K_{C \times E}}$
is equivalent. Hence, identification (11) also holds relatively:
Let
be the connected component corresponding to Quot schemes; that is, flags with
![]() $r = 2$
. By
$r = 2$
. By
we denote its complement. We define
to be the universal quotient and the universal kernel of
![]() ${\rm{Quo}}{{\rm{t}}^{{\rm{rel}}}}( {{\mathsf{a}},{{\mathsf{w}}}})$
, respectively. Quot schemes of stable sheaves on smooth curves are smooth; hence, so are
${\rm{Quo}}{{\rm{t}}^{{\rm{rel}}}}( {{\mathsf{a}},{{\mathsf{w}}}})$
, respectively. Quot schemes of stable sheaves on smooth curves are smooth; hence, so are
![]() ${\rm{Quo}}{{\rm{t}}^{{\rm{rel}}}}( {{\mathsf{a}},{{\mathsf{w}}}})$
by (12).
${\rm{Quo}}{{\rm{t}}^{{\rm{rel}}}}( {{\mathsf{a}},{{\mathsf{w}}}})$
by (12).
4.3 Obstruction theory of flags
By [Reference OberdieckObe21, Section 4], obstruction theories of moduli spaces
![]() ${W^{{\rm{rel}}}}( {{\mathsf{a}},{{\mathsf{w}}}})$
and
${W^{{\rm{rel}}}}( {{\mathsf{a}},{{\mathsf{w}}}})$
and
![]() ${\rm{F}}{{\rm{l}}^{{\rm{rel}}}}( {{\mathsf{a}},{{\mathsf{w}}}})$
also agree. We now describe the obstruction theory of
${\rm{F}}{{\rm{l}}^{{\rm{rel}}}}( {{\mathsf{a}},{{\mathsf{w}}}})$
also agree. We now describe the obstruction theory of
![]() ${\rm{F}}{{\rm{l}}^{{\rm{rel}}}}( {{\mathsf{a}},{{\mathsf{w}}}})$
and the associated virtual normal bundle
${\rm{F}}{{\rm{l}}^{{\rm{rel}}}}( {{\mathsf{a}},{{\mathsf{w}}}})$
and the associated virtual normal bundle
![]() ${N^{{\rm{vir}}}}$
. Let
${N^{{\rm{vir}}}}$
. Let
be the universal flag on
![]() ${K_{C \times E}}\,{ \times _C}\,{\rm{F}}{{\rm{l}}^{{\rm{rel}}}}( {{\mathsf{a}},{{\mathsf{w}}}})$
, and let
${K_{C \times E}}\,{ \times _C}\,{\rm{F}}{{\rm{l}}^{{\rm{rel}}}}( {{\mathsf{a}},{{\mathsf{w}}}})$
, and let
be the natural projection.
Theorem 4.4
The
![]() $C$
-relative obstruction theory of
$C$
-relative obstruction theory of
![]() ${\rm{F}}{{\rm{l}}^{{\rm{rel}}}}( {{\mathsf{a}},{{\mathsf{w}}}})$
is given by the complex
${\rm{F}}{{\rm{l}}^{{\rm{rel}}}}( {{\mathsf{a}},{{\mathsf{w}}}})$
is given by the complex
The
![]() $K$
-class of
$K$
-class of
![]() ${N^{{\rm{vir}}}}$
is
${N^{{\rm{vir}}}}$
is
 \begin{align*} N^{\mathrm{vir}}= &-\sum_{i\geqslant 1}\sum_{k\geqslant 1} R {\mathcal H} om_\pi({\mathcal F}_{i+k}/{\mathcal F}_{i+k-1},{\mathcal F}_i) \mathbf z^{k} \\[3pt] &+ \sum_{i\geqslant 1}\sum_{k\geqslant 1} R {\mathcal H} om_\pi({\mathcal F}_{i+k+1}/{\mathcal F}_{i+k},{\mathcal F}_i)^{\vee}\mathbf z^{-k}. \end{align*}
\begin{align*} N^{\mathrm{vir}}= &-\sum_{i\geqslant 1}\sum_{k\geqslant 1} R {\mathcal H} om_\pi({\mathcal F}_{i+k}/{\mathcal F}_{i+k-1},{\mathcal F}_i) \mathbf z^{k} \\[3pt] &+ \sum_{i\geqslant 1}\sum_{k\geqslant 1} R {\mathcal H} om_\pi({\mathcal F}_{i+k+1}/{\mathcal F}_{i+k},{\mathcal F}_i)^{\vee}\mathbf z^{-k}. \end{align*}
Proof.
See [Reference OberdieckObe21, Section 4]. Note the sign difference in
![]() $z$
-weights; this occurs because
$z$
-weights; this occurs because
![]() $0 \in {\mathbb{P}^1}$
has weight
$0 \in {\mathbb{P}^1}$
has weight
![]() $z$
in contrast with [Reference OberdieckObe21], where its weight is equal to
$z$
in contrast with [Reference OberdieckObe21], where its weight is equal to
![]() $ - z$
.
$ - z$
.
The next lemmas will be useful for the analysis presented in Section 4.6 and in Section 5.
Lemma 4.5. We have the following identity in the K-group,
for some
![]() $K$
-class
$K$
-class
![]() ${\mathsf{K}}$
.
${\mathsf{K}}$
.
Proof.
Let us denote
![]() ${\mathcal{A}}: = {{\mathcal{F}}_{j + 1}}/{{\mathcal{F}}_j}$
and
${\mathcal{A}}: = {{\mathcal{F}}_{j + 1}}/{{\mathcal{F}}_j}$
and
![]() ${\mathcal{B}}: = {{\mathcal{F}}_i}$
. Both
${\mathcal{B}}: = {{\mathcal{F}}_i}$
. Both
![]() ${\mathcal{A}}$
and
${\mathcal{A}}$
and
![]() ${\mathcal{B}}$
are scheme-theoretically supported on the zero section
${\mathcal{B}}$
are scheme-theoretically supported on the zero section
![]() $C \times E \subset {K_{C \times E}}$
; they can therefore be extended to the entire
$C \times E \subset {K_{C \times E}}$
; they can therefore be extended to the entire
![]() ${K_{C \times E}}$
by pulling them back by the projection
${K_{C \times E}}$
by pulling them back by the projection
![]() ${K_{C \times E}} \to C \times E$
. We denote these extensions by
${K_{C \times E}} \to C \times E$
. We denote these extensions by
![]() $\bar {\mathcal{A}}$
and
$\bar {\mathcal{A}}$
and
![]() $\bar {\mathcal{B}}$
.
$\bar {\mathcal{B}}$
.
Consider now the sequence on
![]() ${K_{C \times E}}$
,
${K_{C \times E}}$
,
We tensor it with
![]() $\bar {\mathcal{A}}$
,
$\bar {\mathcal{A}}$
,
and then we apply
![]() $R{\mathcal{H}}o{m_\pi }\!\left( { -, {\mathcal{B}}} \right)$
to obtain the distinguished triangle
$R{\mathcal{H}}o{m_\pi }\!\left( { -, {\mathcal{B}}} \right)$
to obtain the distinguished triangle
There is a natural
![]() $\mathbb{C}_t^{\rm{*}}$
-equivariant identification
$\mathbb{C}_t^{\rm{*}}$
-equivariant identification
which gives us that
Passing to the
![]() $K$
-group, the distinguished triangle (13) therefore gives us that
$K$
-group, the distinguished triangle (13) therefore gives us that
This proves the claim.
Lemma 4.6.
With respect to the identification (12), the obstruction bundle of a Quot scheme
![]() $\mathrm{Quo}{t^{\mathrm{rel}}}({\mathsf{a},\mathsf{w}})$
leads to the following expression:
$\mathrm{Quo}{t^{\mathrm{rel}}}({\mathsf{a},\mathsf{w}})$
leads to the following expression:
Proof.
Assume
![]() $r = 2;$
then
$r = 2;$
then
Using the same distinguished triangle (13) and passing to the associated long exact sequence, we obtain
 \begin{align*}0 & \to {\mathcal{H}}o{m_\pi }\big( {{{\mathcal{K}}^{{\rm{rel}}}},{{\mathcal{Q}}^{{\rm{rel}}}}} \big) \to {\mathcal{H}}o{m_\pi }\big( {{{\bar {\mathcal{K}}}^{{\rm{rel}}}},{{\mathcal{Q}}^{{\rm{rel}}}}} \big) \to {\mathcal{H}}o{m_\pi }\big( {{{\bar {\mathcal{K}}}^{{\rm{rel}}}}\!\left( { - C \times E} \right),{{\mathcal{Q}}^{{\rm{rel}}}}} \big) \to\\& \to {\mathcal{E}}xt_\pi ^1\big( {{{\mathcal{K}}^{{\rm{rel}}}},{{\mathcal{Q}}^{{\rm{rel}}}}} \big) \to {\mathcal{E}}xt_\pi ^1\big( {{{\bar {\mathcal{K}}}^{{\rm{rel}}}},{{\mathcal{Q}}^{{\rm{rel}}}}} \big) \to {\mathcal{E}}xt_\pi ^1\big( {{{\bar {\mathcal{K}}}^{{\rm{rel}}}}\!\left( { - C \times E} \right),{{\mathcal{Q}}^{{\rm{rel}}}}} \big) \to . \ldots \end{align*}
\begin{align*}0 & \to {\mathcal{H}}o{m_\pi }\big( {{{\mathcal{K}}^{{\rm{rel}}}},{{\mathcal{Q}}^{{\rm{rel}}}}} \big) \to {\mathcal{H}}o{m_\pi }\big( {{{\bar {\mathcal{K}}}^{{\rm{rel}}}},{{\mathcal{Q}}^{{\rm{rel}}}}} \big) \to {\mathcal{H}}o{m_\pi }\big( {{{\bar {\mathcal{K}}}^{{\rm{rel}}}}\!\left( { - C \times E} \right),{{\mathcal{Q}}^{{\rm{rel}}}}} \big) \to\\& \to {\mathcal{E}}xt_\pi ^1\big( {{{\mathcal{K}}^{{\rm{rel}}}},{{\mathcal{Q}}^{{\rm{rel}}}}} \big) \to {\mathcal{E}}xt_\pi ^1\big( {{{\bar {\mathcal{K}}}^{{\rm{rel}}}},{{\mathcal{Q}}^{{\rm{rel}}}}} \big) \to {\mathcal{E}}xt_\pi ^1\big( {{{\bar {\mathcal{K}}}^{{\rm{rel}}}}\!\left( { - C \times E} \right),{{\mathcal{Q}}^{{\rm{rel}}}}} \big) \to . \ldots \end{align*}
Since
![]() $Q$
is scheme-theoretically supported on the zero section, the map
$Q$
is scheme-theoretically supported on the zero section, the map
![]() ${\mathcal{H}}o{m_\pi }\big( {{{\bar {\mathcal{K}}}^{{\rm{rel}}}},{{\mathcal{Q}}^{{\rm{rel}}}}} \big) \to {\mathcal{H}}o{m_\pi }( {{{\bar {\mathcal{K}}}^{{\rm{rel}}}}\!\left( { - C \times E} \right),{{\mathcal{Q}}^{{\rm{rel}}}}})$
is zero; hence, the map
${\mathcal{H}}o{m_\pi }\big( {{{\bar {\mathcal{K}}}^{{\rm{rel}}}},{{\mathcal{Q}}^{{\rm{rel}}}}} \big) \to {\mathcal{H}}o{m_\pi }( {{{\bar {\mathcal{K}}}^{{\rm{rel}}}}\!\left( { - C \times E} \right),{{\mathcal{Q}}^{{\rm{rel}}}}})$
is zero; hence, the map
is an isomorphism. This also implies that
is injective. Since we are considering quotients of the stable sheaf
![]() ${\rm{ex}}{{\rm{t}}^2}\left( {K,Q} \right) = 0$
, hence
${\rm{ex}}{{\rm{t}}^2}\left( {K,Q} \right) = 0$
, hence
we conclude that
![]() ${\mathcal{H}}o{m_\pi }( {{{\bar {\mathcal{K}}}^{{\rm{rel}}}}\!\left( { - C \times E} \right),{{\mathcal{Q}}^{{\rm{rel}}}}}) \to {\mathcal{E}}xt_\pi ^1\big( {{{\mathcal{K}}^{{\rm{rel}}}},{{\mathcal{Q}}^{{\rm{rel}}}}} \big)$
is in fact an isomorphism. Using the
${\mathcal{H}}o{m_\pi }( {{{\bar {\mathcal{K}}}^{{\rm{rel}}}}\!\left( { - C \times E} \right),{{\mathcal{Q}}^{{\rm{rel}}}}}) \to {\mathcal{E}}xt_\pi ^1\big( {{{\mathcal{K}}^{{\rm{rel}}}},{{\mathcal{Q}}^{{\rm{rel}}}}} \big)$
is in fact an isomorphism. Using the
![]() $\mathbb{C}_t^{\rm{*}}$
-equivariant identification (14), we obtain that
$\mathbb{C}_t^{\rm{*}}$
-equivariant identification (14), we obtain that
 \begin{align*}{\mathcal{E}}xt_\pi ^1\big( {{{\mathcal{K}}^{{\rm{rel}}}},{{\mathcal{Q}}^{{\rm{rel}}}}} \big) & \cong {\mathcal{H}}o{m_\pi }( {{{\bar {\mathcal{K}}}^{{\rm{rel}}}}\!\left( { - C \times E} \right),{{\mathcal{Q}}^{{\rm{rel}}}}})\\&\cong {\mathcal{H}}o{m_\pi }\big( {{{\bar {\mathcal{K}}}^{{\rm{rel}}}},{{\mathcal{Q}}^{{\rm{rel}}}}} \big) \boxtimes {\omega _C}{\bf{t}} \cong {\mathcal{H}}o{m_\pi } \big( {{{\mathcal{K}}^{{\rm{rel}}}},{{\mathcal{Q}}^{{\rm{rel}}}}} \big) \boxtimes{\omega _C}{\bf{t}}.\end{align*}
\begin{align*}{\mathcal{E}}xt_\pi ^1\big( {{{\mathcal{K}}^{{\rm{rel}}}},{{\mathcal{Q}}^{{\rm{rel}}}}} \big) & \cong {\mathcal{H}}o{m_\pi }( {{{\bar {\mathcal{K}}}^{{\rm{rel}}}}\!\left( { - C \times E} \right),{{\mathcal{Q}}^{{\rm{rel}}}}})\\&\cong {\mathcal{H}}o{m_\pi }\big( {{{\bar {\mathcal{K}}}^{{\rm{rel}}}},{{\mathcal{Q}}^{{\rm{rel}}}}} \big) \boxtimes {\omega _C}{\bf{t}} \cong {\mathcal{H}}o{m_\pi } \big( {{{\mathcal{K}}^{{\rm{rel}}}},{{\mathcal{Q}}^{{\rm{rel}}}}} \big) \boxtimes{\omega _C}{\bf{t}}.\end{align*}
The sheaf
![]() ${\mathcal{H}}o{m_\pi }\big( {{{\mathcal{K}}^{{\rm{rel}}}},{{\mathcal{Q}}^{{\rm{rel}}}}} \big)$
is the
${\mathcal{H}}o{m_\pi }\big( {{{\mathcal{K}}^{{\rm{rel}}}},{{\mathcal{Q}}^{{\rm{rel}}}}} \big)$
is the
![]() $C$
-relative tangent bundle of
$C$
-relative tangent bundle of
![]() ${\rm{Quo}}{{\rm{t}}^{{\rm{rel}}}}( {{\mathsf{a}},{{\mathsf{w}}}})$
, and due to the decomposition (12), its
${\rm{Quo}}{{\rm{t}}^{{\rm{rel}}}}( {{\mathsf{a}},{{\mathsf{w}}}})$
, and due to the decomposition (12), its
![]() $C$
-relative tangent bundle is exactly the pull-back of the tangent bundle of
$C$
-relative tangent bundle is exactly the pull-back of the tangent bundle of
![]() ${\rm{Quot}}( {{\mathsf{a}},{{\mathsf{w}}}})$
.
${\rm{Quot}}( {{\mathsf{a}},{{\mathsf{w}}}})$
.
4.4 Cosections
Cosections of the obstruction theory of
![]() ${\rm{Fl}}{({\mathsf{a}},{{\mathsf{w}}})^{{\rm{rel}}}}$
are constructed in exactly the same way as in [Reference Pandharipande and ThomasPT16, Section 5.4] (see also [Reference OberdieckObe21, Section 4] and [Reference NesterovNes21, Section 10.2]). However, since we work relative to
${\rm{Fl}}{({\mathsf{a}},{{\mathsf{w}}})^{{\rm{rel}}}}$
are constructed in exactly the same way as in [Reference Pandharipande and ThomasPT16, Section 5.4] (see also [Reference OberdieckObe21, Section 4] and [Reference NesterovNes21, Section 10.2]). However, since we work relative to
![]() $C$
, the cosections map is not to a trivial line bundle but to
$C$
, the cosections map is not to a trivial line bundle but to
![]() ${\omega _C}$
. For example, this can already be seen in Lemma 4.6. This is because the relative canonical sheaf of
${\omega _C}$
. For example, this can already be seen in Lemma 4.6. This is because the relative canonical sheaf of
is the pull-back of
![]() $\omega _C^ \vee $
. By the argument from [Reference NesterovNes21, Section 10.2], which uses Serre’s duality, we therefore get a
$\omega _C^ \vee $
. By the argument from [Reference NesterovNes21, Section 10.2], which uses Serre’s duality, we therefore get a
![]() $C$
-relative cosection to
$C$
-relative cosection to
![]() $\omega _C^{ \oplus 2}$
instead of the trivial bundle
$\omega _C^{ \oplus 2}$
instead of the trivial bundle
![]() ${{\mathcal{O}}^{ \oplus 2}}$
(here, we use the identification (9)):
${{\mathcal{O}}^{ \oplus 2}}$
(here, we use the identification (9)):
where
Remark 4.7. By (12), the absolute obstruction theory of
![]() $\mathrm{Fl}^{\mathrm{rel}}( {{\mathsf{a}},{{\mathsf{w}}}})$
is a direct sum of the relative obstruction theory of
$\mathrm{Fl}^{\mathrm{rel}}( {{\mathsf{a}},{{\mathsf{w}}}})$
is a direct sum of the relative obstruction theory of
![]() $\mathrm{Fl}^{\mathrm{rel}}( {{\mathsf{a}},{{\mathsf{w}}}})$
and
$\mathrm{Fl}^{\mathrm{rel}}( {{\mathsf{a}},{{\mathsf{w}}}})$
and
![]() ${T_C}$
. Hence, the cosection constructed above extends to a cosection of the absolute obstruction theory. However, since we are working
${T_C}$
. Hence, the cosection constructed above extends to a cosection of the absolute obstruction theory. However, since we are working
![]() $\mathbb{C}_t^*$
-equivariantly, we do not need to reduce our obstruction theory, as the cosections will manifest themselves only in terms of equivariant parameters in the expressions of virtual fundamental cycles.
$\mathbb{C}_t^*$
-equivariantly, we do not need to reduce our obstruction theory, as the cosections will manifest themselves only in terms of equivariant parameters in the expressions of virtual fundamental cycles.
As in [Reference NesterovNes21, Proposition 10.6], we have the following result:
Proposition 4.8.
The cosection
![]() $\sigma $
is surjective on
$\sigma $
is surjective on
![]() $\mathrm{Quot}^{\mathrm{rel}}{(\mathsf{a},\mathsf{w})^c}$
in
$\mathrm{Quot}^{\mathrm{rel}}{(\mathsf{a},\mathsf{w})^c}$
in
![]() ${W^{\mathrm{rel}}}({\mathsf{a},\mathsf{w}})$
. On
${W^{\mathrm{rel}}}({\mathsf{a},\mathsf{w}})$
. On
![]() $\mathrm{Quot}^{\mathrm{rel}}({\mathsf{a},\mathsf{w}})$
, only the component
$\mathrm{Quot}^{\mathrm{rel}}({\mathsf{a},\mathsf{w}})$
, only the component
![]() ${\sigma _1}$
is surjective.
${\sigma _1}$
is surjective.
Proof. Similar to [Reference Pandharipande and ThomasPT16, Proposition 12].
By the description of the obstruction theory of
![]() ${W^{{\rm{rel}}}}( {{\mathsf{a}},{{\mathsf{w}}}})$
in terms of flags from [Reference OberdieckObe21, Section 4], we can compute its virtual dimension. Indeed, for any two sheaves
${W^{{\rm{rel}}}}( {{\mathsf{a}},{{\mathsf{w}}}})$
in terms of flags from [Reference OberdieckObe21, Section 4], we can compute its virtual dimension. Indeed, for any two sheaves
![]() ${F_1}$
and
${F_1}$
and
![]() ${F_2}$
supported on the zero section of
${F_2}$
supported on the zero section of
![]() ${K_E}$
, we have
${K_E}$
, we have
and the
![]() $C$
-relative virtual dimension of
$C$
-relative virtual dimension of
![]() ${\rm{F}}{{\rm{l}}^{{\rm{rel}}}}( {{\mathsf{a}},{{\mathsf{w}}}})$
is therefore 0. Hence the absolute virtual dimension of
${\rm{F}}{{\rm{l}}^{{\rm{rel}}}}( {{\mathsf{a}},{{\mathsf{w}}}})$
is therefore 0. Hence the absolute virtual dimension of
![]() ${\rm{F}}{{\rm{l}}^{{\rm{rel}}}}( {{\mathsf{a}},{{\mathsf{w}}}})$
is 1.
${\rm{F}}{{\rm{l}}^{{\rm{rel}}}}( {{\mathsf{a}},{{\mathsf{w}}}})$
is 1.
Both the virtual normal bundle and the cosections are
![]() ${{\rm{\Phi }}_{\mathsf{a}}}$
-equivariant by the construction; hence, they descend to the quotients
${{\rm{\Phi }}_{\mathsf{a}}}$
-equivariant by the construction; hence, they descend to the quotients
This, in conjunction with Proposition 4.8, implies that the virtual fundamental cycles of quotients
![]() $\left[ {{\rm{F}}{{\rm{l}}^{{\rm{rel}}}}( {{\mathsf{a}},{{\mathsf{w}}}})/{{\rm{\Phi }}_{\mathsf{a}}}} \right]$
, when restricted to Quot schemes and to their complements, are of the following corollary:
$\left[ {{\rm{F}}{{\rm{l}}^{{\rm{rel}}}}( {{\mathsf{a}},{{\mathsf{w}}}})/{{\rm{\Phi }}_{\mathsf{a}}}} \right]$
, when restricted to Quot schemes and to their complements, are of the following corollary:
Corollary 4.9. We have
 \begin{align*}& {{{[{\rm{Quo}}{{\rm{t}}^{{\rm{rel}}}}( {{\mathsf{a}},{{\mathsf{w}}}})/{{\rm{\Phi }}_{\mathsf{a}}}]}^{{\rm{vir}}}}} {}{ = {\mathsf{B}} \boxtimes [ {{\rm{pt}}}] \in {H_0}\!\left( {W( {{\mathsf{a}},{{\mathsf{w}}}}) \times C,\mathbb{Q}} \right)[t],}\\& {{{[{\rm{Quo}}{{\rm{t}}^{{\rm{rel}}}}( {{\mathsf{a}},{{\mathsf{w}}}})^{c}/{{\rm{\Phi }}_{\mathsf{a}}}]}^{{\rm{vir}}}}} {}{ = {t\mathsf{B}}^{\prime} \boxtimes [ {{\rm{pt}}}] \in {H_2}\!\left( {W( {{\mathsf{a}},{{\mathsf{w}}}}) \times C,\mathbb{Q}} \right)[t],}\end{align*}
\begin{align*}& {{{[{\rm{Quo}}{{\rm{t}}^{{\rm{rel}}}}( {{\mathsf{a}},{{\mathsf{w}}}})/{{\rm{\Phi }}_{\mathsf{a}}}]}^{{\rm{vir}}}}} {}{ = {\mathsf{B}} \boxtimes [ {{\rm{pt}}}] \in {H_0}\!\left( {W( {{\mathsf{a}},{{\mathsf{w}}}}) \times C,\mathbb{Q}} \right)[t],}\\& {{{[{\rm{Quo}}{{\rm{t}}^{{\rm{rel}}}}( {{\mathsf{a}},{{\mathsf{w}}}})^{c}/{{\rm{\Phi }}_{\mathsf{a}}}]}^{{\rm{vir}}}}} {}{ = {t\mathsf{B}}^{\prime} \boxtimes [ {{\rm{pt}}}] \in {H_2}\!\left( {W( {{\mathsf{a}},{{\mathsf{w}}}}) \times C,\mathbb{Q}} \right)[t],}\end{align*}
4.5 Master space
Let
![]() ${\epsilon _0} \in {\mathbb{Q}_{ \gt 0}}$
be a wall of
${\epsilon _0} \in {\mathbb{Q}_{ \gt 0}}$
be a wall of
![]() $\epsilon $
-stabilities for quasisections, and let
$\epsilon $
-stabilities for quasisections, and let
![]() ${\epsilon ^ + }$
and
${\epsilon ^ + }$
and
![]() ${\epsilon ^ - }$
be the values close to the wall
${\epsilon ^ - }$
be the values close to the wall
![]() ${\epsilon _0}$
from the right-hand side and from the left-hand side, respectively. Consider the master space
${\epsilon _0}$
from the right-hand side and from the left-hand side, respectively. Consider the master space
![]() $M{Q^{{\epsilon _0}}}( {{\mathsf{a}},{{\mathsf{w}}}})$
for the wall-crossing around the wall
$M{Q^{{\epsilon _0}}}( {{\mathsf{a}},{{\mathsf{w}}}})$
for the wall-crossing around the wall
![]() ${\epsilon _0};$
we refer to [Reference ZhouZho22, Section 4] for the construction of the master space. Let
${\epsilon _0};$
we refer to [Reference ZhouZho22, Section 4] for the construction of the master space. Let
![]() ${{{\mathsf{w}}}_0} = 1/{\epsilon _0}$
. By construction, there is a
${{{\mathsf{w}}}_0} = 1/{\epsilon _0}$
. By construction, there is a
![]() $\mathbb{C}_z^{\rm{*}}$
-action on
$\mathbb{C}_z^{\rm{*}}$
-action on
![]() $M{Q^{{\epsilon _0}}}( {{\mathsf{a}},{{\mathsf{w}}}})$
. In what follows, we use the identification
$M{Q^{{\epsilon _0}}}( {{\mathsf{a}},{{\mathsf{w}}}})$
. In what follows, we use the identification
Following the terminology of [Reference ZhouZho22], we define
![]() ${\tilde Q^{{\epsilon ^ + }}}( {{\mathsf{a}},{{\mathsf{w}}}})$
to be the pull-back of
${\tilde Q^{{\epsilon ^ + }}}( {{\mathsf{a}},{{\mathsf{w}}}})$
to be the pull-back of
![]() $Q_k^{{\epsilon ^ + }}( {{\mathsf{a}},{{\mathsf{w}}}})$
to the moduli space of entangled semistable degenerations
$Q_k^{{\epsilon ^ + }}( {{\mathsf{a}},{{\mathsf{w}}}})$
to the moduli space of entangled semistable degenerations
![]() ${\tilde{\mathfrak{M}}_{C,k,{{\mathsf{w}}}}}$
, which are constructed in [Reference ZhouZho22, Section 2.2] as a blow-up of the moduli space of weighted semistable degenerations
${\tilde{\mathfrak{M}}_{C,k,{{\mathsf{w}}}}}$
, which are constructed in [Reference ZhouZho22, Section 2.2] as a blow-up of the moduli space of weighted semistable degenerations
![]() ${\mathfrak{M}_{C,k,{{\mathsf{w}}}}}$
,
${\mathfrak{M}_{C,k,{{\mathsf{w}}}}}$
,
We also define
![]() $\tilde Q_k^{{\epsilon ^ + }}( {{\mathsf{a}},{{\mathsf{w}}}})^{\prime}$
to be a
$\tilde Q_k^{{\epsilon ^ + }}( {{\mathsf{a}},{{\mathsf{w}}}})^{\prime}$
to be a
![]() $k$
-root stack of
$k$
-root stack of
![]() $\tilde Q_k^{{\epsilon ^ + }}( {{\mathsf{a}},{{\mathsf{w}}}})$
associated to the calibration bundle
$\tilde Q_k^{{\epsilon ^ + }}( {{\mathsf{a}},{{\mathsf{w}}}})$
associated to the calibration bundle
![]() $\mathbb{M}$
of
$\mathbb{M}$
of
![]() $\tilde Q_k^{{\epsilon ^ + }}( {{\mathsf{a}},{{\mathsf{w}}}})$
, defined in [Reference ZhouZho22, Section 2.8]. By the analysis of [Reference ZhouZho22, Section 6], the
$\tilde Q_k^{{\epsilon ^ + }}( {{\mathsf{a}},{{\mathsf{w}}}})$
, defined in [Reference ZhouZho22, Section 2.8]. By the analysis of [Reference ZhouZho22, Section 6], the
![]() $\mathbb{C}_z^{\rm{*}}$
-fixed locus of
$\mathbb{C}_z^{\rm{*}}$
-fixed locus of
![]() $M{Q^{{\epsilon _0}}}( {{\mathsf{a}},{{\mathsf{w}}}})$
then has the following form,
$M{Q^{{\epsilon _0}}}( {{\mathsf{a}},{{\mathsf{w}}}})$
then has the following form,
such that
![]() ${{\mathsf{w}}} = {{{\mathsf{w}}}_1} + k{{{\mathsf{w}}}_0}$
.
${{\mathsf{w}}} = {{{\mathsf{w}}}_1} + k{{{\mathsf{w}}}_0}$
.
The group
![]() ${{\rm{\Phi }}_{\mathsf{a}}}$
acts on the master space
${{\rm{\Phi }}_{\mathsf{a}}}$
acts on the master space
![]() $M{Q^{{\epsilon _0}}}( {{\mathsf{a}},{{\mathsf{w}}}})$
. Since the action of
$M{Q^{{\epsilon _0}}}( {{\mathsf{a}},{{\mathsf{w}}}})$
. Since the action of
![]() ${{\rm{\Phi }}_{\mathsf{a}}}$
and
${{\rm{\Phi }}_{\mathsf{a}}}$
and
![]() $\mathbb{C}_z^{\rm{*}}$
on
$\mathbb{C}_z^{\rm{*}}$
on
![]() $M{Q^{{\epsilon _0}}}{({\mathsf{a}},{{\mathsf{w}}})^{}}$
commute, the operations of taking the quotient by
$M{Q^{{\epsilon _0}}}{({\mathsf{a}},{{\mathsf{w}}})^{}}$
commute, the operations of taking the quotient by
![]() ${{\rm{\Phi }}_{\mathsf{a}}}$
and taking the
${{\rm{\Phi }}_{\mathsf{a}}}$
and taking the
![]() $\mathbb{C}_z^{\rm{*}}$
-fixed locus also commute. We therefore obtain
$\mathbb{C}_z^{\rm{*}}$
-fixed locus also commute. We therefore obtain
such that the action on the wall-crossing components (the components on the right-hand side in the expression above) is given by the diagonal action of
![]() ${{\rm{\Phi }}_{\mathsf{a}}}$
. By [Reference ZhouZho22, Section 6], the wall-crossing formula is obtained by taking residues of the localisation formula associated with (17). Let
${{\rm{\Phi }}_{\mathsf{a}}}$
. By [Reference ZhouZho22, Section 6], the wall-crossing formula is obtained by taking residues of the localisation formula associated with (17). Let
![]() ${{\mathcal{N}}^{{\rm{vir}}}}$
be the virtual normal bundle of wall-crossing components. The wall-crossing invariants are therefore given by the following residues:
${{\mathcal{N}}^{{\rm{vir}}}}$
be the virtual normal bundle of wall-crossing components. The wall-crossing invariants are therefore given by the following residues:
 \begin{align*}{\rm{Re}}{{\rm{s}}_{z = 0}}{\rm{\;\;}}\left( {\frac{{{{\left[ {\tilde Q_k^{{\epsilon ^ + }}\left( {{\mathsf{a}},{{{\mathsf{w}}}_1}} \right)^{\prime}\,{ \times _{{C^k}}}\,{W^{{\rm{rel}}}}{{({\mathsf{a}},{{{\mathsf{w}}}_0})}^k}/{{\rm{\Phi }}_{\mathsf{a}}}} \right]}^{{\rm{vir}}}}}}{{{e_{\mathbb{C}_{z,t}^{\rm{*}}}}\!\left( {{{\mathcal{N}}^{{\rm{vir}}}}} \right)}}} \right).\end{align*}
\begin{align*}{\rm{Re}}{{\rm{s}}_{z = 0}}{\rm{\;\;}}\left( {\frac{{{{\left[ {\tilde Q_k^{{\epsilon ^ + }}\left( {{\mathsf{a}},{{{\mathsf{w}}}_1}} \right)^{\prime}\,{ \times _{{C^k}}}\,{W^{{\rm{rel}}}}{{({\mathsf{a}},{{{\mathsf{w}}}_0})}^k}/{{\rm{\Phi }}_{\mathsf{a}}}} \right]}^{{\rm{vir}}}}}}{{{e_{\mathbb{C}_{z,t}^{\rm{*}}}}\!\left( {{{\mathcal{N}}^{{\rm{vir}}}}} \right)}}} \right).\end{align*}
We now show that most of the wall-crossing invariants essentially vanish by the second-cosection argument, except that our cosections are twisted, as explained in Section 4.4, which forces us to work a bit harder to obtain the vanishing.
Theorem 4.10.
If
![]() ${\epsilon _0} = 1/{{\mathsf{w}}}$
, then
${\epsilon _0} = 1/{{\mathsf{w}}}$
, then
 \begin{align*}{\rm{deg}}{\Big[{Q^{{\epsilon ^ + }}}{({\mathsf{a}},{{\mathsf{w}}})^ \bullet }\Big]^{{\rm{vir}}}} - {\rm{deg}}{[{Q^{{\epsilon ^ - }}}{({\mathsf{a}},{{\mathsf{w}}})^ \bullet }]^{{\rm{vir}}}} = {\rm{deg\ Re}}{{\rm{s}}_{z = 0}}\left( {\frac{{{{[{\rm{Quo}}{{\rm{t}}^{{\rm{rel}}}}( {{\mathsf{a}},{{\mathsf{w}}}})/{{\rm{\Phi }}_{\mathsf{a}}}]}^{{\rm{vir}}}}}}{{{e_{\mathbb{C}_{z,t}^{\rm{*}}}}\!\left( {{{\mathcal{N}}^{{\rm{vir}}}}} \right)}}} \right).\end{align*}
\begin{align*}{\rm{deg}}{\Big[{Q^{{\epsilon ^ + }}}{({\mathsf{a}},{{\mathsf{w}}})^ \bullet }\Big]^{{\rm{vir}}}} - {\rm{deg}}{[{Q^{{\epsilon ^ - }}}{({\mathsf{a}},{{\mathsf{w}}})^ \bullet }]^{{\rm{vir}}}} = {\rm{deg\ Re}}{{\rm{s}}_{z = 0}}\left( {\frac{{{{[{\rm{Quo}}{{\rm{t}}^{{\rm{rel}}}}( {{\mathsf{a}},{{\mathsf{w}}}})/{{\rm{\Phi }}_{\mathsf{a}}}]}^{{\rm{vir}}}}}}{{{e_{\mathbb{C}_{z,t}^{\rm{*}}}}\!\left( {{{\mathcal{N}}^{{\rm{vir}}}}} \right)}}} \right).\end{align*}
Otherwise,
4.6 Proof of Theorem 4.10
By [Reference ZhouZho22, Section 6], we have to analyse the wall-crossing components in the decomposition (21); see also [Reference NesterovNes21, Section 6], [Reference NesterovNes23, Section 10] and [Reference Lee and WenLW23].
Assuming that
![]() $k \geqslant 2$
or
$k \geqslant 2$
or
![]() ${{{\mathsf{w}}}_1} \ne 0$
, then the space
${{{\mathsf{w}}}_1} \ne 0$
, then the space
has an additional action of
![]() ${{\rm{\Phi }}_{\mathsf{a}}}$
coming from any of the components of the product. To distinguish it from the diagonal action of
${{\rm{\Phi }}_{\mathsf{a}}}$
coming from any of the components of the product. To distinguish it from the diagonal action of
![]() ${{\rm{\Phi }}_{\mathsf{a}}}$
, we denote it by
${{\rm{\Phi }}_{\mathsf{a}}}$
, we denote it by
![]() ${{\rm{\Phi }}^{\prime}_{\mathsf{a}}}$
. The obstruction theory of the quotient
${{\rm{\Phi }}^{\prime}_{\mathsf{a}}}$
. The obstruction theory of the quotient
![]() $\left[ {X/{{\rm{\Phi }}^{\prime}_{\mathsf{a}}}} \right]$
is compatible with the obstruction theory of
$\left[ {X/{{\rm{\Phi }}^{\prime}_{\mathsf{a}}}} \right]$
is compatible with the obstruction theory of
![]() $X$
; hence,
$X$
; hence,
for the quotient map
![]() $\pi :X \to \left[ {X/{{\rm{\Phi }}^{\prime}_{\mathsf{a}}}} \right]$
. Moreover, the virtual normal bundles from [Reference ZhouZho22, Section 6] are
$\pi :X \to \left[ {X/{{\rm{\Phi }}^{\prime}_{\mathsf{a}}}} \right]$
. Moreover, the virtual normal bundles from [Reference ZhouZho22, Section 6] are
![]() ${{\rm{\Phi }}^{\prime}_{\mathsf{a}}}$
-equivariant; hence, they descend to the quotient
${{\rm{\Phi }}^{\prime}_{\mathsf{a}}}$
-equivariant; hence, they descend to the quotient
![]() $\left[ {X/{{\rm{\Phi }}^{\prime}_{\mathsf{a}}}} \right]$
. Overall, we obtain that the wall-crossing class is a pull-back of some class
$\left[ {X/{{\rm{\Phi }}^{\prime}_{\mathsf{a}}}} \right]$
. Overall, we obtain that the wall-crossing class is a pull-back of some class
![]() ${\rm{A}}$
from the quotient
${\rm{A}}$
from the quotient
![]() $\left[ {X/{{\rm{\Phi }}^{\prime}_{\mathsf{a}}}} \right]$
,
$\left[ {X/{{\rm{\Phi }}^{\prime}_{\mathsf{a}}}} \right]$
,
 \begin{align*}\frac{{\left[ {\tilde Q_k^{{\epsilon ^ + }}\!\left( {{\mathsf{a}},{{{\mathsf{w}}}_1}} \right)^{\prime}\,{ \times _{{C^k}}}\,{W^{{\rm{rel}}}}{{({\mathsf{a}},{{{\mathsf{w}}}_0})}^k}/{{\rm{\Phi }}_{\mathsf{a}}}} \right]}}{{{e_{\mathbb{C}_{z,t}^{\rm{*}}}}\!\left( {{{\mathcal{N}}^{{\rm{vir}}}}} \right)}} = {\pi ^{\rm{*}}}{\mathsf{A}};\end{align*}
\begin{align*}\frac{{\left[ {\tilde Q_k^{{\epsilon ^ + }}\!\left( {{\mathsf{a}},{{{\mathsf{w}}}_1}} \right)^{\prime}\,{ \times _{{C^k}}}\,{W^{{\rm{rel}}}}{{({\mathsf{a}},{{{\mathsf{w}}}_0})}^k}/{{\rm{\Phi }}_{\mathsf{a}}}} \right]}}{{{e_{\mathbb{C}_{z,t}^{\rm{*}}}}\!\left( {{{\mathcal{N}}^{{\rm{vir}}}}} \right)}} = {\pi ^{\rm{*}}}{\mathsf{A}};\end{align*}
that its degree is therefore 0 and that it does not contribute to the wall-crossing formula,
 \begin{align*}{\rm{deg\ Re}}{{\rm{s}}_{z = 0}}\left( {\frac{{\left[ {\tilde Q_k^{{\epsilon ^ + }}\left( {{\mathsf{a}},{{{\mathsf{w}}}_1}} \right)^{\prime}\,{ \times _{{C^k}}}\,{W^{{\rm{rel}}}}{{({\mathsf{a}},{{{\mathsf{w}}}_0})}^k}/{{\rm{\Phi }}_{\mathsf{a}}}} \right]}}{{{e_{\mathbb{C}_{z,t}^{\rm{*}}}}\!\left( {{{\mathcal{N}}^{{\rm{vir}}}}} \right)}}} \right) = 0.\end{align*}
\begin{align*}{\rm{deg\ Re}}{{\rm{s}}_{z = 0}}\left( {\frac{{\left[ {\tilde Q_k^{{\epsilon ^ + }}\left( {{\mathsf{a}},{{{\mathsf{w}}}_1}} \right)^{\prime}\,{ \times _{{C^k}}}\,{W^{{\rm{rel}}}}{{({\mathsf{a}},{{{\mathsf{w}}}_0})}^k}/{{\rm{\Phi }}_{\mathsf{a}}}} \right]}}{{{e_{\mathbb{C}_{z,t}^{\rm{*}}}}\!\left( {{{\mathcal{N}}^{{\rm{vir}}}}} \right)}}} \right) = 0.\end{align*}
It remains for us to determine the contribution of terms
Since
![]() $Q_1^ + \left( {{\mathsf{a}},0} \right) = C$
, we obtain that
$Q_1^ + \left( {{\mathsf{a}},0} \right) = C$
, we obtain that
We will now show that the complement of
![]() ${\rm{Quo}}{{\rm{t}}^{{\rm{rel}}}}( {{\mathsf{a}},{{\mathsf{w}}}}) \subset {W^{{\rm{rel}}}}( {{\mathsf{a}},{{\mathsf{w}}}})$
does not contribute. Ideally, one would say that this statement follows from the double cosection argument. However, in this case, the cosections are twisted due to the relative setup; hence, one has to do a little bit of additional work. By [Reference ZhouZho22, Lemma 6.5.6] and the dimension constraint, degrees of the following residues are equal,
${\rm{Quo}}{{\rm{t}}^{{\rm{rel}}}}( {{\mathsf{a}},{{\mathsf{w}}}}) \subset {W^{{\rm{rel}}}}( {{\mathsf{a}},{{\mathsf{w}}}})$
does not contribute. Ideally, one would say that this statement follows from the double cosection argument. However, in this case, the cosections are twisted due to the relative setup; hence, one has to do a little bit of additional work. By [Reference ZhouZho22, Lemma 6.5.6] and the dimension constraint, degrees of the following residues are equal,
 \begin{align}{\rm{deg\ Re}}{{\rm{s}}_{z = 0}}\left( {\frac{{{{[{W^{{\rm{rel}}}}( {{\mathsf{a}},{{\mathsf{w}}}})/{{\rm{\Phi }}_{\mathsf{a}}}]}^{{\rm{vir}}}}}}{{{e_{\mathbb{C}_{z,t}^{\rm{*}}}}\!\left( {{N^{{\rm{vir}}}}} \right)}}} \right) = {\rm{deg\ Re}}{{\rm{s}}_{z = 0}}\left( {\frac{{{{[{W^{{\rm{rel}}}}( {{\mathsf{a}},{{\mathsf{w}}}})/{{\rm{\Phi }}_{\mathsf{a}}}]}^{{\rm{vir}}}}}}{{{e_{\mathbb{C}_{z,t}^{\rm{*}}}}\!\left( {{{\mathcal{N}}^{{\rm{vir}}}}} \right)}}} \right),\end{align}
\begin{align}{\rm{deg\ Re}}{{\rm{s}}_{z = 0}}\left( {\frac{{{{[{W^{{\rm{rel}}}}( {{\mathsf{a}},{{\mathsf{w}}}})/{{\rm{\Phi }}_{\mathsf{a}}}]}^{{\rm{vir}}}}}}{{{e_{\mathbb{C}_{z,t}^{\rm{*}}}}\!\left( {{N^{{\rm{vir}}}}} \right)}}} \right) = {\rm{deg\ Re}}{{\rm{s}}_{z = 0}}\left( {\frac{{{{[{W^{{\rm{rel}}}}( {{\mathsf{a}},{{\mathsf{w}}}})/{{\rm{\Phi }}_{\mathsf{a}}}]}^{{\rm{vir}}}}}}{{{e_{\mathbb{C}_{z,t}^{\rm{*}}}}\!\left( {{{\mathcal{N}}^{{\rm{vir}}}}} \right)}}} \right),\end{align}
where
![]() ${N^{{\rm{vir}}}}$
is the normal bundle of
${N^{{\rm{vir}}}}$
is the normal bundle of
![]() ${W^{{\rm{rel}}}}( {{\mathsf{a}},{{\mathsf{w}}}})$
inside
${W^{{\rm{rel}}}}( {{\mathsf{a}},{{\mathsf{w}}}})$
inside
![]() $GQ( {{\mathsf{a}},{{\mathsf{w}}}})$
, whose expression is given in Theorem 4.4.
$GQ( {{\mathsf{a}},{{\mathsf{w}}}})$
, whose expression is given in Theorem 4.4.
We argue that
![]() ${\rm{Quo}}{{\rm{t}}^{{\rm{rel}}}}{({\mathsf{a}},{{\mathsf{w}}})^c} \subset {W^{{\rm{rel}}}}( {{\mathsf{a}},{{\mathsf{w}}}})$
does not contribute because the quantity (18) is a multiple of
${\rm{Quo}}{{\rm{t}}^{{\rm{rel}}}}{({\mathsf{a}},{{\mathsf{w}}})^c} \subset {W^{{\rm{rel}}}}( {{\mathsf{a}},{{\mathsf{w}}}})$
does not contribute because the quantity (18) is a multiple of
![]() ${t^2}$
. As taking quotient by
${t^2}$
. As taking quotient by
![]() ${{\rm{\Phi }}_{\mathsf{a}}}$
can be exchanged with taking an insertion, it is enough to show that (18) is a multiple of
${{\rm{\Phi }}_{\mathsf{a}}}$
can be exchanged with taking an insertion, it is enough to show that (18) is a multiple of
![]() ${t^2}$
before taking quotient. By Corollary 4.6, we know that
${t^2}$
before taking quotient. By Corollary 4.6, we know that
![]() ${[{\rm{Quo}}{{\rm{t}}^{{\rm{rel}}}}{({\mathsf{a}},{{\mathsf{w}}})^c}]^{{\rm{vir}}}}$
is a multiple of
${[{\rm{Quo}}{{\rm{t}}^{{\rm{rel}}}}{({\mathsf{a}},{{\mathsf{w}}})^c}]^{{\rm{vir}}}}$
is a multiple of
![]() $t$
, and we therefore have to show that the residue of
$t$
, and we therefore have to show that the residue of
![]() ${e_{\mathbb{C}_{z,t}^{\rm{*}}}}{({N^{{\rm{vir}}}})^{ - 1}}$
is a multiple of
${e_{\mathbb{C}_{z,t}^{\rm{*}}}}{({N^{{\rm{vir}}}})^{ - 1}}$
is a multiple of
![]() $t$
, too. By Theorem 4.4, the class
$t$
, too. By Theorem 4.4, the class
![]() ${e_{\mathbb{C}_{z,t}^{\rm{*}}}}{({N^{{\rm{vir}}}})^{ - 1}}$
leads to the following expression:
${e_{\mathbb{C}_{z,t}^{\rm{*}}}}{({N^{{\rm{vir}}}})^{ - 1}}$
leads to the following expression:
 \begin{align} e_{{\mathbb{C}}_{z,t}^*}(N^{\mathrm{vir}})^{-1}&= \prod_{i\geqslant 1, k\geqslant 1} \frac{e_{{\mathbb{C}}_{z,t}^*} ( R {\mathcal H} om_{\pi}({\mathcal F}_{i+k}/{\mathcal F}_{i+k-1},{\mathcal F}_i) \mathbf z^{k})}{e_{{\mathbb{C}}_{z,t}^*} ( R {\mathcal H} om_{\pi}({\mathcal F}_{i+k+1}/ {\mathcal F}_{i+k},{\mathcal F}_i)^{\vee} \mathbf z^{-k})} .\end{align}
\begin{align} e_{{\mathbb{C}}_{z,t}^*}(N^{\mathrm{vir}})^{-1}&= \prod_{i\geqslant 1, k\geqslant 1} \frac{e_{{\mathbb{C}}_{z,t}^*} ( R {\mathcal H} om_{\pi}({\mathcal F}_{i+k}/{\mathcal F}_{i+k-1},{\mathcal F}_i) \mathbf z^{k})}{e_{{\mathbb{C}}_{z,t}^*} ( R {\mathcal H} om_{\pi}({\mathcal F}_{i+k+1}/ {\mathcal F}_{i+k},{\mathcal F}_i)^{\vee} \mathbf z^{-k})} .\end{align}
According to (15), the rank of
![]() $R{\mathcal{H}}o{m_\pi }\!\left( {{{\mathcal{F}}_{i + k}}/{{\mathcal{F}}_{i + k - 1}},{{\mathcal{F}}_i}} \right)$
is 0; hence,
$R{\mathcal{H}}o{m_\pi }\!\left( {{{\mathcal{F}}_{i + k}}/{{\mathcal{F}}_{i + k - 1}},{{\mathcal{F}}_i}} \right)$
is 0; hence,
 \begin{align*}e_{{\mathbb{C}}_{z,t}^*} ( R {\mathcal H} om_{\pi}({\mathcal F}_{i+k} /{\mathcal F}_{i+k-1},{\mathcal F}_i) \otimes \mathbf z^{k}) &=\sum_{j\geqslant 0}(kz)^{-j}\mathrm{c}_j(R {\mathcal H} om_{\pi}({\mathcal F}_{i+k} /{\mathcal F}_{i+k-1},{\mathcal F}_i)) \\ &=1-(kz)^{-1}\mathrm{c}_1(R {\mathcal H} om_{\pi}({\mathcal F}_{i+k+1} /{\mathcal F}_{i+k},{\mathcal F}_i))+ O(z^{-2}), \end{align*}
\begin{align*}e_{{\mathbb{C}}_{z,t}^*} ( R {\mathcal H} om_{\pi}({\mathcal F}_{i+k} /{\mathcal F}_{i+k-1},{\mathcal F}_i) \otimes \mathbf z^{k}) &=\sum_{j\geqslant 0}(kz)^{-j}\mathrm{c}_j(R {\mathcal H} om_{\pi}({\mathcal F}_{i+k} /{\mathcal F}_{i+k-1},{\mathcal F}_i)) \\ &=1-(kz)^{-1}\mathrm{c}_1(R {\mathcal H} om_{\pi}({\mathcal F}_{i+k+1} /{\mathcal F}_{i+k},{\mathcal F}_i))+ O(z^{-2}), \end{align*}
the same applies to the denominator of (19). We therefore obtain that
 \begin{align} e_{{\mathbb{C}}_{z,t}^*}(N^{\mathrm{vir}})^{-1} & = 1-\sum_{i,k} (kz)^{-1}\mathrm{c}_1(R {\mathcal H} om_{\pi}({\mathcal F}_{i+k} /{\mathcal F}_{i+k-1},F_i))\nonumber\\& - \sum_{i,k} (kz)^{-1}\mathrm{c}_1(R {\mathcal H} om_{\pi}({\mathcal F}_{i+k+1} /{\mathcal F}_{i+k},{\mathcal F}_i))^{\vee} + O(z^{-2}). \end{align}
\begin{align} e_{{\mathbb{C}}_{z,t}^*}(N^{\mathrm{vir}})^{-1} & = 1-\sum_{i,k} (kz)^{-1}\mathrm{c}_1(R {\mathcal H} om_{\pi}({\mathcal F}_{i+k} /{\mathcal F}_{i+k-1},F_i))\nonumber\\& - \sum_{i,k} (kz)^{-1}\mathrm{c}_1(R {\mathcal H} om_{\pi}({\mathcal F}_{i+k+1} /{\mathcal F}_{i+k},{\mathcal F}_i))^{\vee} + O(z^{-2}). \end{align}
By Lemma 4.5, we obtain that
for some class
![]() ${\mathsf{A}}$
of cohomological degree 0. Using Corollary 4.6 and (20), we conclude that
${\mathsf{A}}$
of cohomological degree 0. Using Corollary 4.6 and (20), we conclude that
 \begin{align*}{\rm{Re}}{{\rm{s}}_{z = 0}}\left( {\frac{{{{[{\rm{Quo}}{{\rm{t}}^{{\rm{rel}}}}{{({\mathsf{a}},{{\mathsf{w}}})}^c}]}^{{\rm{vir}}}}}}{{{e_{\mathbb{C}_{z,t}^{\rm{*}}}}\!\left( {{N^{{\rm{vir}}}}} \right)}}} \right) = {\mathsf{A}^{\prime}}{t^2} \in {H_2}\!\left( {{\rm{Quo}}{{\rm{t}}^c},\mathbb{Q}} \right)[t],\end{align*}
\begin{align*}{\rm{Re}}{{\rm{s}}_{z = 0}}\left( {\frac{{{{[{\rm{Quo}}{{\rm{t}}^{{\rm{rel}}}}{{({\mathsf{a}},{{\mathsf{w}}})}^c}]}^{{\rm{vir}}}}}}{{{e_{\mathbb{C}_{z,t}^{\rm{*}}}}\!\left( {{N^{{\rm{vir}}}}} \right)}}} \right) = {\mathsf{A}^{\prime}}{t^2} \in {H_2}\!\left( {{\rm{Quo}}{{\rm{t}}^c},\mathbb{Q}} \right)[t],\end{align*}
for some class
![]() ${\mathsf{A}^{\prime}}$
of homological degree 2. Taking the degree of the class above, we obtain 0. This finishes the proof of Theorem 4.10.
${\mathsf{A}^{\prime}}$
of homological degree 2. Taking the degree of the class above, we obtain 0. This finishes the proof of Theorem 4.10.
4.7 Contributions from Quot schemes
We now have to determine the contributions of
![]() ${\rm{Quo}}{{\rm{t}}^{{\rm{rel}}}}( {{\mathsf{a}},{{\mathsf{w}}}}) \subset {W^{{\rm{rel}}}}( {{\mathsf{a}},{{\mathsf{w}}}})$
. Firstly, by [Reference OberdieckObe21, Section 4], the component
${\rm{Quo}}{{\rm{t}}^{{\rm{rel}}}}( {{\mathsf{a}},{{\mathsf{w}}}}) \subset {W^{{\rm{rel}}}}( {{\mathsf{a}},{{\mathsf{w}}}})$
. Firstly, by [Reference OberdieckObe21, Section 4], the component
![]() ${\rm{Quo}}{{\rm{t}}^{{\rm{rel}}}}( {{\mathsf{a}},{{\mathsf{w}}}}) \subset {W^{{\rm{rel}}}}( {{\mathsf{a}},{{\mathsf{w}}}})$
is composed of the following Quot schemes
${\rm{Quo}}{{\rm{t}}^{{\rm{rel}}}}( {{\mathsf{a}},{{\mathsf{w}}}}) \subset {W^{{\rm{rel}}}}( {{\mathsf{a}},{{\mathsf{w}}}})$
is composed of the following Quot schemes
and the classes
![]() ${u_{\rm{m}}}$
are defined as follows:
${u_{\rm{m}}}$
are defined as follows:
where
![]() $\check{\mathsf{w}} $
is given by (7) and
$\check{\mathsf{w}} $
is given by (7) and
![]() ${h_{\mathsf{m}}}$
is the unique integer such that
${h_{\mathsf{m}}}$
is the unique integer such that
We therefore obtain the following proposition:
Proposition 4.11. We have
Proof. See [Reference OberdieckObe21, Section 4].
Let us analyse
![]() ${N^{{\rm{vir}}}}$
over each component
${N^{{\rm{vir}}}}$
over each component
![]() $\left[ {{\rm{Quo}}{{\rm{t}}^{{\rm{rel}}}}\!\left( {{\mathsf{a}},{u_{\rm{m}}}} \right)\!/{{\rm{\Phi }}_{\mathsf{a}}}} \right]$
. In what follows, we use the notation from Section 5. By [Reference OberdieckObe21, Section 4.4], the equivariant Euler class of the virtual normal bundle
$\left[ {{\rm{Quo}}{{\rm{t}}^{{\rm{rel}}}}\!\left( {{\mathsf{a}},{u_{\rm{m}}}} \right)\!/{{\rm{\Phi }}_{\mathsf{a}}}} \right]$
. In what follows, we use the notation from Section 5. By [Reference OberdieckObe21, Section 4.4], the equivariant Euler class of the virtual normal bundle
![]() ${N^{{\rm{vir}}}}$
can be expressed as follows:
${N^{{\rm{vir}}}}$
can be expressed as follows:
 \begin{align*}{e_{\mathbb{C}_{z,t}^{\rm{*}}}}{({N^{{\rm{vir}}}})^{ - 1}} & = {e_{\mathbb{C}_{z,t}^{*}}}\!\big( {R{\mathcal{H}}o{m_\pi }\big( {{{\mathcal{Q}}^{{\rm{rel}}}},{{\mathcal{K}}^{{\rm{rel}}}}} \big){{\bf{z}}^{\mathsf{m}}}} \big)\\& = {e_{\mathbb{C}_{z,t}^{\rm{*}}}}\!\big(R{\mathcal{H}}o{m_\pi }\big( {{\mathcal{K}}^{{\rm{rel}}}},{{\mathcal{Q}}^{{\rm{rel}}}}\big){^ \vee }{\bf{t}}{{\bf{z}}^{\mathsf{m}}} \big)\\ {}&=\sum_{k \in {\mathbb{Z}}}({\mathsf{m}} z)^{-k}\mathrm{c}_{k}(R{\mathcal H} om_\pi({\mathcal K}^{\mathrm{rel}},{\mathcal Q}^{\mathrm{rel}})^{\vee}\mathbf t),\end{align*}
\begin{align*}{e_{\mathbb{C}_{z,t}^{\rm{*}}}}{({N^{{\rm{vir}}}})^{ - 1}} & = {e_{\mathbb{C}_{z,t}^{*}}}\!\big( {R{\mathcal{H}}o{m_\pi }\big( {{{\mathcal{Q}}^{{\rm{rel}}}},{{\mathcal{K}}^{{\rm{rel}}}}} \big){{\bf{z}}^{\mathsf{m}}}} \big)\\& = {e_{\mathbb{C}_{z,t}^{\rm{*}}}}\!\big(R{\mathcal{H}}o{m_\pi }\big( {{\mathcal{K}}^{{\rm{rel}}}},{{\mathcal{Q}}^{{\rm{rel}}}}\big){^ \vee }{\bf{t}}{{\bf{z}}^{\mathsf{m}}} \big)\\ {}&=\sum_{k \in {\mathbb{Z}}}({\mathsf{m}} z)^{-k}\mathrm{c}_{k}(R{\mathcal H} om_\pi({\mathcal K}^{\mathrm{rel}},{\mathcal Q}^{\mathrm{rel}})^{\vee}\mathbf t),\end{align*}
where
![]() ${{\mathcal{K}}^{{\rm{rel}}}}$
and
${{\mathcal{K}}^{{\rm{rel}}}}$
and
![]() ${{\mathcal{Q}}^{{\rm{rel}}}}$
are as in Section 4.2. We are interested in the residue of
${{\mathcal{Q}}^{{\rm{rel}}}}$
are as in Section 4.2. We are interested in the residue of
![]() ${e_{\mathbb{C}_{z,t}^{\rm{*}}}}{({N^{{\rm{vir}}}})^{ - 1}}$
,
${e_{\mathbb{C}_{z,t}^{\rm{*}}}}{({N^{{\rm{vir}}}})^{ - 1}}$
,
 \begin{align*}{\rm{Re}}{{\rm{s}}_{z = 0}}({e_{\mathbb{C}_{z,t}^{\rm{*}}}}\!\left( {{N^{{\rm{vir}}}}{)^{ - 1}}} \right) & = {{\mathsf{m}}^{ - 1}}{{\rm{c}}_1}\big(R{\mathcal{H}}o{m_\pi }( {{\mathcal{K}}^{{\rm{rel}}}},{{\mathcal{Q}}^{{\rm{rel}}}}){^ \vee }{\bf{t}} \big)\\&= {{\mathsf{m}}^{ - 1}}{\rm{rk}}\big({\mathcal{H}}o{m_\pi }( {{\mathcal{K}}^{{\rm{rel}}}},{{\mathcal{Q}}^{{\rm{rel}}}}){^ \vee } \big)( {{{\rm{c}}_1}( {{\omega _C}}) + t} )\\&= {{\mathsf{m}}^{ - 1}}\,{\rm{dim}}\!\left( {{\rm{Quot}}( {{\mathsf{a}},{u_{\mathsf{m}}}})} \right)\left( {{{\rm{c}}_1}( {{\omega _C}}) + t} \right).\end{align*}
\begin{align*}{\rm{Re}}{{\rm{s}}_{z = 0}}({e_{\mathbb{C}_{z,t}^{\rm{*}}}}\!\left( {{N^{{\rm{vir}}}}{)^{ - 1}}} \right) & = {{\mathsf{m}}^{ - 1}}{{\rm{c}}_1}\big(R{\mathcal{H}}o{m_\pi }( {{\mathcal{K}}^{{\rm{rel}}}},{{\mathcal{Q}}^{{\rm{rel}}}}){^ \vee }{\bf{t}} \big)\\&= {{\mathsf{m}}^{ - 1}}{\rm{rk}}\big({\mathcal{H}}o{m_\pi }( {{\mathcal{K}}^{{\rm{rel}}}},{{\mathcal{Q}}^{{\rm{rel}}}}){^ \vee } \big)( {{{\rm{c}}_1}( {{\omega _C}}) + t} )\\&= {{\mathsf{m}}^{ - 1}}\,{\rm{dim}}\!\left( {{\rm{Quot}}( {{\mathsf{a}},{u_{\mathsf{m}}}})} \right)\left( {{{\rm{c}}_1}( {{\omega _C}}) + t} \right).\end{align*}
Using Corollary 4.9, the total residue then takes the following form:
 \begin{align*}{\rm{Re}}{{\rm{s}}_{z = 0}}\left( {\frac{{{{[{\rm{Quo}}{{\rm{t}}^{{\rm{rel}}}}( {{\mathsf{a}},{u_{\mathsf{m}}}})/{{\rm{\Phi }}_{\mathsf{a}}}]}^{{\rm{vir}}}}}}{{{e_{\mathbb{C}_{z,t}^{\rm{*}}}}\!\left( {{N^{{\rm{vir}}}}} \right)}}} \right) = {{\mathsf{m}}^{ - 1}}\,{\rm{dim}}\!\left( {{\rm{Quot}}( {{\mathsf{a}},{u_{\mathsf{m}}}})} \right){[{\rm{Quo}}{{\rm{t}}^{{\rm{rel}}}}( {{\mathsf{a}},{u_{\mathsf{m}}}})/{{\rm{\Phi }}_{\mathsf{a}}}]^{{\rm{vir}}}}t.\end{align*}
\begin{align*}{\rm{Re}}{{\rm{s}}_{z = 0}}\left( {\frac{{{{[{\rm{Quo}}{{\rm{t}}^{{\rm{rel}}}}( {{\mathsf{a}},{u_{\mathsf{m}}}})/{{\rm{\Phi }}_{\mathsf{a}}}]}^{{\rm{vir}}}}}}{{{e_{\mathbb{C}_{z,t}^{\rm{*}}}}\!\left( {{N^{{\rm{vir}}}}} \right)}}} \right) = {{\mathsf{m}}^{ - 1}}\,{\rm{dim}}\!\left( {{\rm{Quot}}( {{\mathsf{a}},{u_{\mathsf{m}}}})} \right){[{\rm{Quo}}{{\rm{t}}^{{\rm{rel}}}}( {{\mathsf{a}},{u_{\mathsf{m}}}})/{{\rm{\Phi }}_{\mathsf{a}}}]^{{\rm{vir}}}}t.\end{align*}
Assume that
![]() $( {{\mathsf{r}},{\mathsf{a}}}) = ( {2,1});$
using the analysis from Corollaries 5.3 and 5.4, we get
$( {{\mathsf{r}},{\mathsf{a}}}) = ( {2,1});$
using the analysis from Corollaries 5.3 and 5.4, we get
 \begin{align*}{\rm{deg\ Re}}{{\rm{s}}_{z = 0}}\left( {\frac{{{{[{\rm{Quo}}{{\rm{t}}^{{\rm{rel}}}}( {{\mathsf{a}},{u_{\mathsf{m}}}})/{{\rm{\Phi }}_{\mathsf{a}}}]}^{{\rm{vir}}}}}}{{{e_{{\mathbb{C}^{\rm{*}}}}}\!\left( {{N^{{\rm{vir}}}}} \right)}}} \right) = ( {2g - 2}){{\mathsf{m}}^{ - 1}}t.\end{align*}
\begin{align*}{\rm{deg\ Re}}{{\rm{s}}_{z = 0}}\left( {\frac{{{{[{\rm{Quo}}{{\rm{t}}^{{\rm{rel}}}}( {{\mathsf{a}},{u_{\mathsf{m}}}})/{{\rm{\Phi }}_{\mathsf{a}}}]}^{{\rm{vir}}}}}}{{{e_{{\mathbb{C}^{\rm{*}}}}}\!\left( {{N^{{\rm{vir}}}}} \right)}}} \right) = ( {2g - 2}){{\mathsf{m}}^{ - 1}}t.\end{align*}
Now, applying Theorem 4.10 repeatedly and using the fact that
![]() ${Q^ + }( {{\mathsf{a}},{{\mathsf{w}}}})$
is empty for
${Q^ + }( {{\mathsf{a}},{{\mathsf{w}}}})$
is empty for
![]() ${{\mathsf{w}}} \ne 0$
, we obtain the following result (for how
${{\mathsf{w}}} \ne 0$
, we obtain the following result (for how
![]() ${\mathsf{d}}$
and
${\mathsf{d}}$
and
![]() ${{\mathsf{w}}}$
are related, see (7)):
${{\mathsf{w}}}$
are related, see (7)):
Theorem 4.12.
If
![]() $( {{\mathsf{r}},{\mathsf{a}}}) = ( {2,1})$
, then
$( {{\mathsf{r}},{\mathsf{a}}}) = ( {2,1})$
, then
 \begin{align*} \mathsf{QM} (E)_{1, \mathsf{w} }^{{\mathsf{d}}, \bullet}=\begin{cases} (2g-2) \sum_{{\mathsf{m}}| \mathsf{w} }{\mathsf{m}}^{-1}t, \quad &\text{ if } \mathsf{w} ={\mathsf{d}} \ \mathrm{mod}\ 2 \\ 0, &\text{ otherwise.} \end{cases}\end{align*}
\begin{align*} \mathsf{QM} (E)_{1, \mathsf{w} }^{{\mathsf{d}}, \bullet}=\begin{cases} (2g-2) \sum_{{\mathsf{m}}| \mathsf{w} }{\mathsf{m}}^{-1}t, \quad &\text{ if } \mathsf{w} ={\mathsf{d}} \ \mathrm{mod}\ 2 \\ 0, &\text{ otherwise.} \end{cases}\end{align*}
Using Corollary 3.7, we obtain the desired quasimap invariants.
Theorem 4.13.
If
![]() $\left( {\mathsf{r},\mathsf{a}} \right) = ( {2,1})$
, then
$\left( {\mathsf{r},\mathsf{a}} \right) = ( {2,1})$
, then
 \begin{align*} \mathsf{QM} (C)_{{\mathsf{d}},\mathsf{w} }^{1, \bullet} = \begin{cases} (2g-2)2^{2g} \sum_{{\mathsf{m}}| \mathsf{w} }{\mathsf{m}}^{-1}t, \quad &\text{ if } \mathsf{w} ={\mathsf{d}} \ \mathrm{mod}\ 2 \\ 0, &\text{ otherwise.} \end{cases} \end{align*}
\begin{align*} \mathsf{QM} (C)_{{\mathsf{d}},\mathsf{w} }^{1, \bullet} = \begin{cases} (2g-2)2^{2g} \sum_{{\mathsf{m}}| \mathsf{w} }{\mathsf{m}}^{-1}t, \quad &\text{ if } \mathsf{w} ={\mathsf{d}} \ \mathrm{mod}\ 2 \\ 0, &\text{ otherwise.} \end{cases} \end{align*}
This gives us Theorems 1.1 and 1.2 (after passing to reduced invariants; that is, after dividing by
![]() $t$
).
$t$
).
Remark 4.14. Since
![]() ${M_E}(1) = \left\{ {\left( {G,0} \right)} \right\}$
, invariants
${M_E}(1) = \left\{ {\left( {G,0} \right)} \right\}$
, invariants
![]() $\mathsf{QM}(C)_{\mathsf{d},\mathsf{w}}^{1, \bullet }$
have only instanton contributions; that is, on
$\mathsf{QM}(C)_{\mathsf{d},\mathsf{w}}^{1, \bullet }$
have only instanton contributions; that is, on
![]() $C$
they correspond to invariants of moduli spaces of stable bundles
$C$
they correspond to invariants of moduli spaces of stable bundles
![]() ${T^*}{N_C}(\mathsf{d}) \subset {M_C}(\mathsf{d})$
. On the other hand, the even-degree invariants are completely monopole; that is, they correspond to invariants of the complement of
${T^*}{N_C}(\mathsf{d}) \subset {M_C}(\mathsf{d})$
. On the other hand, the even-degree invariants are completely monopole; that is, they correspond to invariants of the complement of
![]() ${N_C}(\mathsf{d})$
in the nilpotent cone. This was expected from [Reference Manschot and MooreMM21]; see also [Reference NesterovNes23, Remark 7.2].
${N_C}(\mathsf{d})$
in the nilpotent cone. This was expected from [Reference Manschot and MooreMM21]; see also [Reference NesterovNes23, Remark 7.2].
Remark 4.15. Let us now comment on the fact that genus 1 Gromov–Witten invariants of
![]() $E$
have very similar expressions, as was mentioned in the introduction. If
$E$
have very similar expressions, as was mentioned in the introduction. If
![]() $\mathrm{gcd}({{\mathsf{r}},{\mathsf{d}}}) = 1$
, then a moduli space of stable sheaves on
$\mathrm{gcd}({{\mathsf{r}},{\mathsf{d}}}) = 1$
, then a moduli space of stable sheaves on
![]() $E$
is naturally isomorphic to
$E$
is naturally isomorphic to
![]() $E$
via the determinant map. Hence, Gromov–Witten theory of
$E$
via the determinant map. Hence, Gromov–Witten theory of
![]() $E$
is equivalent to one of its moduli spaces of sheaves. Here, we study a kind of twisted Gromov–Witten theory of moduli spaces of sheaves on
$E$
is equivalent to one of its moduli spaces of sheaves. Here, we study a kind of twisted Gromov–Witten theory of moduli spaces of sheaves on
![]() $E$
. Hence, (posteriori) it is not so unexpected that we get similar answers. Perhaps this phenomenon can be made even precise.
$E$
. Hence, (posteriori) it is not so unexpected that we get similar answers. Perhaps this phenomenon can be made even precise.
4.8 Higher rank
By (7), if we assume that all divisors
![]() ${\mathsf{m}}$
of
${\mathsf{m}}$
of
![]() ${{\mathsf{w}}}$
are congruent to
${{\mathsf{w}}}$
are congruent to
![]() $0$
or
$0$
or
![]() ${\mathsf{a}}$
modulo
${\mathsf{a}}$
modulo
![]() ${\mathsf{r}}$
, then
${\mathsf{r}}$
, then
therefore, using the arguments of the previous section, the analysis of Section 5.2 is enough to conclude the following:
Proposition 4.16.
If
![]() ${\mathsf{r}}$
is prime,
${\mathsf{r}}$
is prime,
![]() ${\mathsf{a}} \ne 0$
and all divisors
${\mathsf{a}} \ne 0$
and all divisors
![]() ${\mathsf{m}}$
of
${\mathsf{m}}$
of
![]() ${{\mathsf{w}}}$
satisfy
${{\mathsf{w}}}$
satisfy
then
 \begin{align*}\mathsf{QM} (C)_{{\mathsf{d}},\mathsf{w} }^{{\mathsf{a}}, \bullet} = \begin{cases} (2g-2){\mathsf{r}}^{2g} \sum_{{\mathsf{m}}| \mathsf{w} }{\mathsf{m}}^{-1}t, \quad &\text{ if } \mathsf{w} = {\mathsf{d}} \cdot {\mathsf{a}} \ \mathrm{mod}\ {\mathsf{r}} \\ 0, &\text{ otherwise.} \end{cases} \end{align*}
\begin{align*}\mathsf{QM} (C)_{{\mathsf{d}},\mathsf{w} }^{{\mathsf{a}}, \bullet} = \begin{cases} (2g-2){\mathsf{r}}^{2g} \sum_{{\mathsf{m}}| \mathsf{w} }{\mathsf{m}}^{-1}t, \quad &\text{ if } \mathsf{w} = {\mathsf{d}} \cdot {\mathsf{a}} \ \mathrm{mod}\ {\mathsf{r}} \\ 0, &\text{ otherwise.} \end{cases} \end{align*}
This agrees with [Reference NesterovNes23, Conjecture E]. Our methods involving Quot schemes lead to an obvious conjectural extension of Proposition 4.16:
Conjecture 4.17.
If
![]() $\mathrm{gcd}(\mathsf{r}, \mathsf{a}) = 1$
, then
$\mathrm{gcd}(\mathsf{r}, \mathsf{a}) = 1$
, then
 \begin{align*} \mathsf{QM} (C)_{{\mathsf{a}}, \mathsf{w} }^{{\mathsf{d}}, \bullet}=\begin{cases} (2g-2) {\mathsf{r}}^{2g}\sum_{{\mathsf{m}}| \mathsf{w} }{\mathsf{m}}^{-1}t, \quad &\text{ if } \mathsf{w} ={\mathsf{d}} \cdot {\mathsf{a}} \ \mathrm{mod}\ {\mathsf{r}} \\ 0, &\text{ otherwise.} \end{cases} \end{align*}
\begin{align*} \mathsf{QM} (C)_{{\mathsf{a}}, \mathsf{w} }^{{\mathsf{d}}, \bullet}=\begin{cases} (2g-2) {\mathsf{r}}^{2g}\sum_{{\mathsf{m}}| \mathsf{w} }{\mathsf{m}}^{-1}t, \quad &\text{ if } \mathsf{w} ={\mathsf{d}} \cdot {\mathsf{a}} \ \mathrm{mod}\ {\mathsf{r}} \\ 0, &\text{ otherwise.} \end{cases} \end{align*}
5. Quot schemes
5.1 Group actions on Quot schemes
The group
![]() ${{\rm{\Phi }}_{\mathsf{a}}}$
acts naturally on Quot schemes
${{\rm{\Phi }}_{\mathsf{a}}}$
acts naturally on Quot schemes
![]() ${\rm{Quot}}( {{\mathsf{a}},{{\mathsf{w}}}})$
. The stabilisers of the action are finite, as long as
${\rm{Quot}}( {{\mathsf{a}},{{\mathsf{w}}}})$
. The stabilisers of the action are finite, as long as
![]() ${{\mathsf{w}}} \ne 0$
. The quotient stack
${{\mathsf{w}}} \ne 0$
. The quotient stack
![]() $\left[ {{\rm{Quot}}( {{\mathsf{a}},{{\mathsf{w}}}})/{{\rm{\Phi }}_{\mathsf{a}}}} \right]$
is therefore a Deligne–Mumford stack. Taking the quotient respects the identification (12),
$\left[ {{\rm{Quot}}( {{\mathsf{a}},{{\mathsf{w}}}})/{{\rm{\Phi }}_{\mathsf{a}}}} \right]$
is therefore a Deligne–Mumford stack. Taking the quotient respects the identification (12),
The obstruction theory of
![]() $\left[ {{\rm{Quo}}{{\rm{t}}^{{\rm{rel}}}}( {{\mathsf{a}},{{\mathsf{w}}}})/{{\rm{\Phi }}_{\mathsf{a}}}} \right]$
is a descent of the obstruction theory of
$\left[ {{\rm{Quo}}{{\rm{t}}^{{\rm{rel}}}}( {{\mathsf{a}},{{\mathsf{w}}}})/{{\rm{\Phi }}_{\mathsf{a}}}} \right]$
is a descent of the obstruction theory of
![]() $\left[ {{\rm{Quo}}{{\rm{t}}^{{\rm{rel}}}}( {{\mathsf{a}},{{\mathsf{w}}}})} \right]$
. By Lemma 4.6, the
$\left[ {{\rm{Quo}}{{\rm{t}}^{{\rm{rel}}}}( {{\mathsf{a}},{{\mathsf{w}}}})} \right]$
. By Lemma 4.6, the
![]() $C$
-relative obstruction bundle of the quotient is therefore given by the descent of
$C$
-relative obstruction bundle of the quotient is therefore given by the descent of
![]() ${T_{{\rm{Quot}}( {{\mathsf{a}},{{\mathsf{w}}}})}} \boxtimes {\omega _C}{\bf{t}}$
. More precisely, let
${T_{{\rm{Quot}}( {{\mathsf{a}},{{\mathsf{w}}}})}} \boxtimes {\omega _C}{\bf{t}}$
. More precisely, let
be the quotient map; then we have the
![]() ${{\rm{\Phi }}_{\mathsf{a}}}$
-equivariant identification
${{\rm{\Phi }}_{\mathsf{a}}}$
-equivariant identification
such that
![]() ${\rm{O}}{{\rm{b}}_{{\rm{Quo}}{{\rm{t}}^{{\rm{rel}}}}( {{\mathsf{a}},{{\mathsf{w}}}})}}$
is
${\rm{O}}{{\rm{b}}_{{\rm{Quo}}{{\rm{t}}^{{\rm{rel}}}}( {{\mathsf{a}},{{\mathsf{w}}}})}}$
is
![]() ${{\rm{\Phi }}_{\mathsf{a}}}$
-equivariantly isomorphic to
${{\rm{\Phi }}_{\mathsf{a}}}$
-equivariantly isomorphic to
![]() ${T_{{\rm{Quot}}( {{\mathsf{a}},{{\mathsf{w}}}})}}\boxtimes {\omega _C}{\bf{t}}$
. We will denote the descent of
${T_{{\rm{Quot}}( {{\mathsf{a}},{{\mathsf{w}}}})}}\boxtimes {\omega _C}{\bf{t}}$
. We will denote the descent of
![]() ${T_{{\rm{Quot}}( {{\mathsf{a}},{{\mathsf{w}}}})}}$
to
${T_{{\rm{Quot}}( {{\mathsf{a}},{{\mathsf{w}}}})}}$
to
![]() $\left[ {{\rm{Quot}}( {{\mathsf{a}},{{\mathsf{w}}}})/{{\rm{\Phi }}_{\mathsf{a}}}} \right]$
by the same symbol. Hence, by Lemma 4.6, we obtain the following corollary:
$\left[ {{\rm{Quot}}( {{\mathsf{a}},{{\mathsf{w}}}})/{{\rm{\Phi }}_{\mathsf{a}}}} \right]$
by the same symbol. Hence, by Lemma 4.6, we obtain the following corollary:
Corollary 5.1.
There is a natural identification on
![]() $\left[ {\mathrm{Quot}^{\mathrm{rel}}({\mathsf{a},\mathsf{w}})/{\Phi _{\mathsf{a}}}} \right]$
,
$\left[ {\mathrm{Quot}^{\mathrm{rel}}({\mathsf{a},\mathsf{w}})/{\Phi _{\mathsf{a}}}} \right]$
,
We are now ready to determine the virtual degree.
Proposition 5.2.
For any
![]() ${\mathsf{r}}$
and
${\mathsf{r}}$
and
![]() ${\mathsf{a}}$
, we have
${\mathsf{a}}$
, we have
Proof. Considering the map
the associated sequence of tangent complexes takes the following form:
Since
![]() ${T_{{{\rm{\Phi }}_{\mathsf{a}}}}}$
is trivial, we obtain that
${T_{{{\rm{\Phi }}_{\mathsf{a}}}}}$
is trivial, we obtain that
 \begin{align*}e\left( T_{[{\rm{Quot}}( {{\mathsf{a}},{{\mathsf{w}}}}) ]}\right) & = 0,\\{{\rm{c}}_{{\mathsf{rk}} - 1}}\left( T_{[{\rm{Quot}}( {{\mathsf{a}},{{\mathsf{w}}}}) ]}\right) & = e\!\left( {{T_{\left[ {{\rm{Quot}}( {{\mathsf{a}},{{\mathsf{w}}}})/{{\rm{\Phi }}_{\mathsf{a}}}} \right]}}} \right).\end{align*}
\begin{align*}e\left( T_{[{\rm{Quot}}( {{\mathsf{a}},{{\mathsf{w}}}}) ]}\right) & = 0,\\{{\rm{c}}_{{\mathsf{rk}} - 1}}\left( T_{[{\rm{Quot}}( {{\mathsf{a}},{{\mathsf{w}}}}) ]}\right) & = e\!\left( {{T_{\left[ {{\rm{Quot}}( {{\mathsf{a}},{{\mathsf{w}}}})/{{\rm{\Phi }}_{\mathsf{a}}}} \right]}}} \right).\end{align*}
Using Corollary 5.1, we therefore obtain
 \begin{align*}{[{\rm{Quo}}{{\rm{t}}^{{\rm{rel}}}}( {{\mathsf{a}},{{\mathsf{w}}}})/{{\rm{\Phi }}_{\mathsf{a}}}]^{{\rm{vir}}}} &= {e_{\mathbb{C}_t^{\rm{*}}}}\!\left( {{\rm{O}}{{\rm{b}}_{\left[ {{\rm{Quo}}{{\rm{t}}^{{\rm{rel}}}}( {{\mathsf{a}},{{\mathsf{w}}}})/{{\rm{\Phi }}_{\mathsf{a}}}} \right]}}} \right)\\&= e\!\left( {{T_{{\rm{Quot}}( {{\mathsf{a}},{{\mathsf{w}}}})}}} \right) + {{\rm{c}}_{{\rm{rk}} - 1}}\!\left( {T_{[{\rm{Quot}}( {{\mathsf{a}},{{\mathsf{w}}}}) ]}}\right) \cdot ( {{{\rm{c}}_1}( {{\omega _C}} ) - t} ) + \ldots\\&= e\!\left( {{T_{\left[ {{\rm{Quot}}( {{\mathsf{a}},{{\mathsf{w}}}})/{{\rm{\Phi }}_{\mathsf{a}}}} \right]}}} \right) \cdot ( {{{\rm{c}}_1}( {{\omega _C}} ) - t} ) + \ldots .\end{align*}
\begin{align*}{[{\rm{Quo}}{{\rm{t}}^{{\rm{rel}}}}( {{\mathsf{a}},{{\mathsf{w}}}})/{{\rm{\Phi }}_{\mathsf{a}}}]^{{\rm{vir}}}} &= {e_{\mathbb{C}_t^{\rm{*}}}}\!\left( {{\rm{O}}{{\rm{b}}_{\left[ {{\rm{Quo}}{{\rm{t}}^{{\rm{rel}}}}( {{\mathsf{a}},{{\mathsf{w}}}})/{{\rm{\Phi }}_{\mathsf{a}}}} \right]}}} \right)\\&= e\!\left( {{T_{{\rm{Quot}}( {{\mathsf{a}},{{\mathsf{w}}}})}}} \right) + {{\rm{c}}_{{\rm{rk}} - 1}}\!\left( {T_{[{\rm{Quot}}( {{\mathsf{a}},{{\mathsf{w}}}}) ]}}\right) \cdot ( {{{\rm{c}}_1}( {{\omega _C}} ) - t} ) + \ldots\\&= e\!\left( {{T_{\left[ {{\rm{Quot}}( {{\mathsf{a}},{{\mathsf{w}}}})/{{\rm{\Phi }}_{\mathsf{a}}}} \right]}}} \right) \cdot ( {{{\rm{c}}_1}( {{\omega _C}} ) - t} ) + \ldots .\end{align*}
Taking the degree, we arrive at the statement of the proposition,
We now have to compute
![]() $e\!\left( {{T_{\left[ {{\rm{Quot}}( {{\mathsf{a}},{{\mathsf{w}}}})/{{\rm{\Phi }}_{\mathsf{a}}}} \right]}}} \right)$
. The analysis might be split, depending on the Chern character of quotients in the decomposition (21).
$e\!\left( {{T_{\left[ {{\rm{Quot}}( {{\mathsf{a}},{{\mathsf{w}}}})/{{\rm{\Phi }}_{\mathsf{a}}}} \right]}}} \right)$
. The analysis might be split, depending on the Chern character of quotients in the decomposition (21).
5.2 Relevant Quot schemes
For this section we assume that
![]() ${\mathsf{a}} \ne 0$
. Consider firstly the class
${\mathsf{a}} \ne 0$
. Consider firstly the class
Let
then
![]() ${\rm{Quot}}( {{\mathsf{a}},u})$
is a
${\rm{Quot}}( {{\mathsf{a}},u})$
is a
![]() ${\mathbb{P}^{{\mathsf{dim}} - 1}}$
-bundle over
${\mathbb{P}^{{\mathsf{dim}} - 1}}$
-bundle over
![]() ${\rm{Jac}}(E)$
given by the natural projection
${\rm{Jac}}(E)$
given by the natural projection
A fiber
is a slice of the
![]() ${{\rm{\Phi }}_{\mathsf{a}}}$
-action on
${{\rm{\Phi }}_{\mathsf{a}}}$
-action on
![]() ${\rm{Quot}}( {{\mathsf{a}},u})$
. In other words, let
${\rm{Quot}}( {{\mathsf{a}},u})$
. In other words, let
![]() ${{\rm{\Gamma }}_{\mathsf{k}}} \subset {{\rm{\Phi }}_{\mathsf{a}}}$
be a finite subgroup that fixes
${{\rm{\Gamma }}_{\mathsf{k}}} \subset {{\rm{\Phi }}_{\mathsf{a}}}$
be a finite subgroup that fixes
![]() ${\mathbb{P}^{{\mathsf{dim}} - 1}}$
, then we have the following diagram:
${\mathbb{P}^{{\mathsf{dim}} - 1}}$
, then we have the following diagram:

The diagram above gives us that
It therefore remains to determine
![]() ${{\rm{\Gamma }}_{\mathsf{k}}}$
. The subgroup
${{\rm{\Gamma }}_{\mathsf{k}}}$
. The subgroup
![]() ${{\rm{\Gamma }}_{\mathsf{k}}} \subset {{\rm{\Phi }}_{\mathsf{a}}}$
that fixes the slice is exactly the subgroup that fixes a line bundle
${{\rm{\Gamma }}_{\mathsf{k}}} \subset {{\rm{\Phi }}_{\mathsf{a}}}$
that fixes the slice is exactly the subgroup that fixes a line bundle
![]() ${\mathcal{O}}( {{\mathsf{a}} - {\mathsf{k}}})$
of degree
${\mathcal{O}}( {{\mathsf{a}} - {\mathsf{k}}})$
of degree
![]() ${\mathsf{a}} - {\mathsf{k}}$
. A translation of
${\mathsf{a}} - {\mathsf{k}}$
. A translation of
![]() ${\mathcal{O}}( {{\mathsf{a}} - {\mathsf{k}}})$
by
${\mathcal{O}}( {{\mathsf{a}} - {\mathsf{k}}})$
by
![]() ${\tau _p}$
that is associated to a point
${\tau _p}$
that is associated to a point
![]() $p \in E$
can be described as follows:
$p \in E$
can be described as follows:
where
![]() ${L_p}$
is line bundle corresponding to
${L_p}$
is line bundle corresponding to
![]() $p$
under the natural identification
$p$
under the natural identification
 \begin{align*}E & \mathop\to\limits^{\cong} {\rm{Jac}}(E)\\p & \mapsto {\mathcal{O}}\!\left( {{0_E}} \right) \otimes {\mathcal{O}}{(p)^{ - 1}} = :{L_p}.\end{align*}
\begin{align*}E & \mathop\to\limits^{\cong} {\rm{Jac}}(E)\\p & \mapsto {\mathcal{O}}\!\left( {{0_E}} \right) \otimes {\mathcal{O}}{(p)^{ - 1}} = :{L_p}.\end{align*}
By the definition of
![]() ${{\rm{\Phi }}_{\mathsf{a}}}$
from (2), determining the stabiliser of
${{\rm{\Phi }}_{\mathsf{a}}}$
from (2), determining the stabiliser of
![]() ${\mathcal{O}}( {{\mathsf{a}} - {\mathsf{k}}})$
in
${\mathcal{O}}( {{\mathsf{a}} - {\mathsf{k}}})$
in
![]() ${{\rm{\Phi }}_{\mathsf{a}}}$
therefore amounts to finding pairs
${{\rm{\Phi }}_{\mathsf{a}}}$
therefore amounts to finding pairs
such that
Raising the expression to the power of
![]() ${\mathsf{r}}$
, we conclude that
${\mathsf{r}}$
, we conclude that
![]() $L_p^{{\mathsf{dim}}} = {{\mathcal{O}}_E}$
. As a group,
$L_p^{{\mathsf{dim}}} = {{\mathcal{O}}_E}$
. As a group,
![]() $E$
is isomorphic to
$E$
is isomorphic to
![]() $\mathbb{R}/\mathbb{Z} \times \mathbb{R}/\mathbb{Z}$
; hence, with respect to the identification
$\mathbb{R}/\mathbb{Z} \times \mathbb{R}/\mathbb{Z}$
; hence, with respect to the identification
![]() $E \cong \mathbb{R}/\mathbb{Z} \times \mathbb{R}/\mathbb{Z}$
, we obtain that
$E \cong \mathbb{R}/\mathbb{Z} \times \mathbb{R}/\mathbb{Z}$
, we obtain that
and that
![]() $\mathsf{r}$
-roots of
$\mathsf{r}$
-roots of
![]() ${a_i} = \frac{{{n_i}}}{{{\mathsf{dim}}}}$
are given by the following elements:
${a_i} = \frac{{{n_i}}}{{{\mathsf{dim}}}}$
are given by the following elements:
However, only one satisfies the equation
more specifically,
![]() $h$
is uniquely defined by the following equation:
$h$
is uniquely defined by the following equation:
We therefore conclude that for all
![]() $p \in E$
, there exists a unique root
$p \in E$
, there exists a unique root
![]() $L_p^{\frac{{\mathsf{a}}}{{\mathsf{r}}}}$
that satisfies the equation (23) and that it must be
$L_p^{\frac{{\mathsf{a}}}{{\mathsf{r}}}}$
that satisfies the equation (23) and that it must be
![]() ${\mathsf{dim}}$
-torsion; hence
${\mathsf{dim}}$
-torsion; hence
![]() $p$
is also
$p$
is also
![]() ${\mathsf{dim}}$
-torsion. We therefore obtain that
${\mathsf{dim}}$
-torsion. We therefore obtain that
or, in particular, that
Proposition 5.2 and (22) give us the following:
Corollary 5.3.
If
![]() $u = ( {\mathsf{r} - 1,\mathsf{k}})$
, then
$u = ( {\mathsf{r} - 1,\mathsf{k}})$
, then
Consider now the class
In this case,
and
![]() ${\rm{Quot}}( {{\mathsf{a}},u})$
admits the natural projection
${\rm{Quot}}( {{\mathsf{a}},u})$
admits the natural projection
which provides a slice of the action of
![]() ${{\rm{\Phi }}_{\mathsf{a}}}$
on
${{\rm{\Phi }}_{\mathsf{a}}}$
on
![]() ${\rm{Quot}}( {{\mathsf{a}},u})$
. More specifically, let
${\rm{Quot}}( {{\mathsf{a}},u})$
. More specifically, let
be the fibre of the projection, and let
![]() ${{\rm{\Gamma }}_{\mathsf{k}}} \subset {{\rm{\Phi }}_{\mathsf{a}}}$
be the stabiliser of
${{\rm{\Gamma }}_{\mathsf{k}}} \subset {{\rm{\Phi }}_{\mathsf{a}}}$
be the stabiliser of
![]() ${\rm{Quot}}{({\rm{a}},u)_0}$
. We obtain that
${\rm{Quot}}{({\rm{a}},u)_0}$
. We obtain that
The subgroup
![]() ${{\rm{\Gamma }}_{\mathsf{k}}} \in {{\rm{\Phi }}_{\mathsf{a}}}$
that fixes the slice is exactly the subgroup that fixes the determinant of a
${{\rm{\Gamma }}_{\mathsf{k}}} \in {{\rm{\Phi }}_{\mathsf{a}}}$
that fixes the slice is exactly the subgroup that fixes the determinant of a
![]() $0$
-dimension sheaf of degree
$0$
-dimension sheaf of degree
![]() ${\mathsf{k}}$
; this means that it consists of pairs
${\mathsf{k}}$
; this means that it consists of pairs
such that
hence,
Let us now determine the Euler characteristics of
![]() ${\rm{Quot}}{({\mathsf{a}},u)_0}$
. Firstly, any vector bundle on a curve can be deformed to a direct sum of line bundles. By the deformation invariance of the (virtual) Euler characteristics, we can assume that
${\rm{Quot}}{({\mathsf{a}},u)_0}$
. Firstly, any vector bundle on a curve can be deformed to a direct sum of line bundles. By the deformation invariance of the (virtual) Euler characteristics, we can assume that
![]() $G = \oplus _{i = 1}^{i = {\mathsf{r}}}{L_i}$
. In this case,
$G = \oplus _{i = 1}^{i = {\mathsf{r}}}{L_i}$
. In this case,
![]() ${\rm{Quot}}{({\mathsf{a}},u)_0}$
admits a torus-action of
${\rm{Quot}}{({\mathsf{a}},u)_0}$
admits a torus-action of
![]() $T= \prod^{i={\mathsf{r}} }_{i=1} {\mathbb{C}}^*$
acting by scaling line bundles. The associated fixed locus has the following description:
$T= \prod^{i={\mathsf{r}} }_{i=1} {\mathbb{C}}^*$
acting by scaling line bundles. The associated fixed locus has the following description:
 \begin{align*} \mathrm{Quot}({\mathsf{a}}, u )_0^T= \coprod_{u_1\substack{+\dots +}u_{\mathsf{r}}=u} \left( \prod^{i={\mathsf{r}}}_{i=1} \mathrm{Quot}(L_i,u_i)\right)_0, \end{align*}
\begin{align*} \mathrm{Quot}({\mathsf{a}}, u )_0^T= \coprod_{u_1\substack{+\dots +}u_{\mathsf{r}}=u} \left( \prod^{i={\mathsf{r}}}_{i=1} \mathrm{Quot}(L_i,u_i)\right)_0, \end{align*}
we refer to [Reference Monavari and RicolfiMR22, Section 3] for more details in case of usual Quot schemes, which extend in a straightforward manner to our slices. Let us now analyse Euler characteristics of the components in the decomposition above. Firstly, if at least two class
![]() ${u_k}$
and
${u_k}$
and
![]() ${u_j}$
are nonzero, then
${u_j}$
are nonzero, then
![]() $\left( \prod_i \mathrm{Quot}(L_i,u_i)\right)_0$
admits an extra fixed-point-free action of
$\left( \prod_i \mathrm{Quot}(L_i,u_i)\right)_0$
admits an extra fixed-point-free action of
![]() $E$
; therefore,
$E$
; therefore,
 \begin{align*} \chi\!\left( \left(\prod^{i={\mathsf{r}}}_{i=1}\mathrm{Quot}(L_i,u_i)\right)_0\right)=0, \quad \text{ if }u_k\neq 0 \text{ and } u_j \neq 0 . \end{align*}
\begin{align*} \chi\!\left( \left(\prod^{i={\mathsf{r}}}_{i=1}\mathrm{Quot}(L_i,u_i)\right)_0\right)=0, \quad \text{ if }u_k\neq 0 \text{ and } u_j \neq 0 . \end{align*}
If only one class
![]() ${u_j}$
is nonzero, then
${u_j}$
is nonzero, then
 \begin{align*}\left( \prod^{i={\mathsf{r}}}_{i=1} \mathrm{Quot}(L_i,u_i)\right)_0= \mathrm{Quot}(L_{j},u_{j})_0= {\mathbb{P}}^{{\mathsf{k}}-1}.\end{align*}
\begin{align*}\left( \prod^{i={\mathsf{r}}}_{i=1} \mathrm{Quot}(L_i,u_i)\right)_0= \mathrm{Quot}(L_{j},u_{j})_0= {\mathbb{P}}^{{\mathsf{k}}-1}.\end{align*}
We therefore obtain
 \begin{align*} \chi\!\left( \left( \prod^{i={\mathsf{r}}}_{i=1}\mathrm{Quot}(L_i,u_i)\right)_0\right)={\mathsf{k}}, \quad \text{ if only one } u_{j}\neq 0. \end{align*}
\begin{align*} \chi\!\left( \left( \prod^{i={\mathsf{r}}}_{i=1}\mathrm{Quot}(L_i,u_i)\right)_0\right)={\mathsf{k}}, \quad \text{ if only one } u_{j}\neq 0. \end{align*}
Overall,
Combining Proposition 5.2, (24) and (25), we obtain the following:
Corollary 5.4.
If
![]() $u = \left( {0,\mathsf{k}} \right)$
, then
$u = \left( {0,\mathsf{k}} \right)$
, then
Acknowledgements
I am grateful to Sanghyeon Lee and Yaoxiong Wen for useful discussions on related topics, during which the idea of using quasisections was conceived, and to Martijn Kool and Richard Thomas for answering various questions on Vafa–Witten theory. I also thank the anonymous referee for their helpful comments.
Conflicts of Interest
None.
Funding Statement
This work is a part of a project that has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No. 101001159).
Journal Information
Moduli is published as a joint venture of the Foundation Compositio Mathematica and the London Mathematical Society. As not-for-profit organisations, the Foundation and Society reinvest
![]() $100\%$
of any surplus generated from their publications back into mathematics through their charitable activities.
$100\%$
of any surplus generated from their publications back into mathematics through their charitable activities.