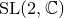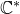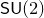1. Introduction
Let
![]() $\Sigma$
be a closed Riemann surface of genus
$\Sigma$
be a closed Riemann surface of genus
![]() $g\geq 2$
. The coarse Dolbeault moduli space of
$g\geq 2$
. The coarse Dolbeault moduli space of
![]() ${\rm SL}(2,\mathbb{C})$
semistable Higgs bundles on
${\rm SL}(2,\mathbb{C})$
semistable Higgs bundles on
![]() $\Sigma$
, denoted by
$\Sigma$
, denoted by
![]() $\mathcal{M}_{{\rm Dol}}$
, and Hitchin’s moduli space of solutions to the
$\mathcal{M}_{{\rm Dol}}$
, and Hitchin’s moduli space of solutions to the
![]() $\mathsf{SU}(2)$
self-duality equations on
$\mathsf{SU}(2)$
self-duality equations on
![]() $\Sigma$
, denoted by
$\Sigma$
, denoted by
![]() $\mathcal{M}_{{\rm Hit}}$
, have been extensively studied since their introduction more than 35 years ago. The Kobayashi–Hitchin correspondence, proved in [Reference HitchinHit87a], gives a homeomorphism between these two moduli spaces:
$\mathcal{M}_{{\rm Hit}}$
, have been extensively studied since their introduction more than 35 years ago. The Kobayashi–Hitchin correspondence, proved in [Reference HitchinHit87a], gives a homeomorphism between these two moduli spaces:
Both spaces are noncompact:
![]() $\mathcal{M}_{{\rm Dol}}$
is naturally a quasiprojective variety [Reference NitsureNit91, Reference SimpsonSim94], and like monopole moduli spaces,
$\mathcal{M}_{{\rm Dol}}$
is naturally a quasiprojective variety [Reference NitsureNit91, Reference SimpsonSim94], and like monopole moduli spaces,
![]() $\mathcal{M}_{{\rm Hit}}$
admits Higgs fields of arbitrarily large norms. Nevertheless, the map
$\mathcal{M}_{{\rm Hit}}$
admits Higgs fields of arbitrarily large norms. Nevertheless, the map
![]() $\Xi$
is proper. Recently, there has been interest from several directions on natural compactifications of these two spaces. A key feature on the Dolbeault side is the existence of a
$\Xi$
is proper. Recently, there has been interest from several directions on natural compactifications of these two spaces. A key feature on the Dolbeault side is the existence of a
![]() $\mathbb{C}^\ast$
action with the Białynicki–Birula property, and this may be used to define a completion of
$\mathbb{C}^\ast$
action with the Białynicki–Birula property, and this may be used to define a completion of
![]() $\mathcal{M}_{{\rm Dol}}$
as a projective variety [Reference HauselHau98, Reference de CataldodC21, Reference FanFan22a]. The ideal points are identified with the
$\mathcal{M}_{{\rm Dol}}$
as a projective variety [Reference HauselHau98, Reference de CataldodC21, Reference FanFan22a]. The ideal points are identified with the
![]() $\mathbb{C}^*$
orbits in the complement of the nilpotent cone of
$\mathbb{C}^*$
orbits in the complement of the nilpotent cone of
![]() $\mathcal{M}_{{\rm Dol}}$
. The Hitchin moduli space also admits a more recently introduced compactification,
$\mathcal{M}_{{\rm Dol}}$
. The Hitchin moduli space also admits a more recently introduced compactification,
![]() $\overline{\mathcal{M}}_{{\rm Hit}}$
, based on the work of several authors (see [Reference Mazzeo, Swoboda, Weiss and WittMSWW16, Reference MochizukiMoc16, Reference TaubesTau13b]). The boundary of
$\overline{\mathcal{M}}_{{\rm Hit}}$
, based on the work of several authors (see [Reference Mazzeo, Swoboda, Weiss and WittMSWW16, Reference MochizukiMoc16, Reference TaubesTau13b]). The boundary of
![]() $\overline{\mathcal{M}}_{{\rm Hit}}$
is given by gauge equivalence classes of limiting configurations. This compactification is relevant to many aspects of Hitchin’s moduli space. For more details, we refer the reader to [Reference Dumas and NeitzkeDN19, Reference Mazzeo, Swoboda, Weiß and WittMSWW14, Reference FredricksonFre20, Reference Fredrickson, Mazzeo, Swoboda and WeissFMSW22, Reference Ott, Swoboda, Wentworth and WolfOSWW20, Reference Katzarkov, Noll, Pandit and SimpsonKNPS15, Reference Chen and LiCL22] and to the references therein.
$\overline{\mathcal{M}}_{{\rm Hit}}$
is given by gauge equivalence classes of limiting configurations. This compactification is relevant to many aspects of Hitchin’s moduli space. For more details, we refer the reader to [Reference Dumas and NeitzkeDN19, Reference Mazzeo, Swoboda, Weiß and WittMSWW14, Reference FredricksonFre20, Reference Fredrickson, Mazzeo, Swoboda and WeissFMSW22, Reference Ott, Swoboda, Wentworth and WolfOSWW20, Reference Katzarkov, Noll, Pandit and SimpsonKNPS15, Reference Chen and LiCL22] and to the references therein.
By the work of [Reference Mazzeo, Swoboda, Weiss and WittMSWW16, Reference MochizukiMoc16], there is a natural extension
of the Kobayashi–Hitchin correspondence to the two compactifications described above, and it is of interest to study the geometry of this map. Doing so involves another key feature of Hitchin’s moduli space; namely, spectral curves. Spectral curves and spectral data [Reference HitchinHit92] realise the Dolbeault moduli space as an algebraically complete integrable system
![]() $\mathcal{H}: \mathcal{M}_{{\rm Dol}}\to \mathcal{B}$
. In the case of
$\mathcal{H}: \mathcal{M}_{{\rm Dol}}\to \mathcal{B}$
. In the case of
![]() ${\rm SL}(2,\mathbb{C})$
, the base
${\rm SL}(2,\mathbb{C})$
, the base
![]() $\mathcal B$
is the space of holomorphic quadratic differentials on
$\mathcal B$
is the space of holomorphic quadratic differentials on
![]() $\Sigma$
. Given
$\Sigma$
. Given
![]() $q\in H^0(K^2)$
, one obtains a (scheme theoretic) spectral curve
$q\in H^0(K^2)$
, one obtains a (scheme theoretic) spectral curve
![]() $S_q$
. This curve is reduced if
$S_q$
. This curve is reduced if
![]() $q\neq 0$
, is irreducible if
$q\neq 0$
, is irreducible if
![]() $q$
is not the square of an abelian differential, and is smooth if
$q$
is not the square of an abelian differential, and is smooth if
![]() $q$
has simple zeros. Let
$q$
has simple zeros. Let
![]() $\mathcal{B}^{\textrm{reg}}\subset \mathcal{B}$
denote the open cone of quadratic differentials with simple zeros.
$\mathcal{B}^{\textrm{reg}}\subset \mathcal{B}$
denote the open cone of quadratic differentials with simple zeros.
The ideal points of both compactifications
![]() $\overline{\mathcal{M}}_{{\rm Dol}}$
and
$\overline{\mathcal{M}}_{{\rm Dol}}$
and
![]() $\overline{\mathcal{M}}_{{\rm Hit}}$
have associated nonzero quadratic differentials and, therefore, spectral curves. We write
$\overline{\mathcal{M}}_{{\rm Hit}}$
have associated nonzero quadratic differentials and, therefore, spectral curves. We write
![]() $\overline{\mathcal{M}}_{{\rm Dol}}^{{\rm reg}}$
for the elements in
$\overline{\mathcal{M}}_{{\rm Dol}}^{{\rm reg}}$
for the elements in
![]() $\overline{\mathcal{M}}_{{\rm Dol}}$
with smooth spectral curves and
$\overline{\mathcal{M}}_{{\rm Dol}}$
with smooth spectral curves and
![]() $\overline{\mathcal{M}}_{{\rm Dol}}^{{\rm sing}}=\overline{\mathcal{M}}_{{\rm Dol}}\setminus \overline{\mathcal{M}}_{{\rm Dol}}^{{\rm reg}}$
for those with singular spectral curves; similarly for
$\overline{\mathcal{M}}_{{\rm Dol}}^{{\rm sing}}=\overline{\mathcal{M}}_{{\rm Dol}}\setminus \overline{\mathcal{M}}_{{\rm Dol}}^{{\rm reg}}$
for those with singular spectral curves; similarly for
![]() $\overline{\mathcal{M}}_{{\rm Hit}}^{{\rm reg}}$
and
$\overline{\mathcal{M}}_{{\rm Hit}}^{{\rm reg}}$
and
![]() $\overline{\mathcal{M}}_{{\rm Hit}}^{{\rm sing}}$
. We then have the following result:
$\overline{\mathcal{M}}_{{\rm Hit}}^{{\rm sing}}$
. We then have the following result:
Theorem 1.1.
The restriction of the compactified Kobayashi–Hitchin map
![]() $\overline{\Xi }$
to the locus with smooth associated spectral curves defines a homeomorphism
$\overline{\Xi }$
to the locus with smooth associated spectral curves defines a homeomorphism
![]() $\overline{\mathcal{M}}_{{\rm Dol}}^{{\rm reg}}\simeq \overline{\mathcal{M}}_{{\rm Hit}}^{{\rm reg}}$
. On the singular spectral curve locus, however,
$\overline{\mathcal{M}}_{{\rm Dol}}^{{\rm reg}}\simeq \overline{\mathcal{M}}_{{\rm Hit}}^{{\rm reg}}$
. On the singular spectral curve locus, however,
![]() $\overline{\Xi }^{{\rm sing}}:\overline{\mathcal{M}}_{{\rm Dol}}^{{\rm sing}}\to \overline{\mathcal{M}}_{{\rm Hit}}^{{\rm sing}}$
is neither surjective nor injective.
$\overline{\Xi }^{{\rm sing}}:\overline{\mathcal{M}}_{{\rm Dol}}^{{\rm sing}}\to \overline{\mathcal{M}}_{{\rm Hit}}^{{\rm sing}}$
is neither surjective nor injective.
It will be convenient to analyse the behavior along rays in
![]() $\mathcal{B}$
, where the spectral curve is simply rescaled. For
$\mathcal{B}$
, where the spectral curve is simply rescaled. For
![]() $q\neq 0$
(a quadratic differential), we set
$q\neq 0$
(a quadratic differential), we set
![]() $\overline{\mathcal{M}}_{{\rm Dol},q^+}$
(resp.
$\overline{\mathcal{M}}_{{\rm Dol},q^+}$
(resp.
![]() $\overline{\mathcal{M}}_{{\rm Hit},q^+}$
) to be the points in
$\overline{\mathcal{M}}_{{\rm Hit},q^+}$
) to be the points in
![]() $\overline{\mathcal{M}}_{{\rm Dol}}$
(resp.
$\overline{\mathcal{M}}_{{\rm Dol}}$
(resp.
![]() $\overline{\mathcal{M}}_{{\rm Hit}}$
) with spectral curves
$\overline{\mathcal{M}}_{{\rm Hit}}$
) with spectral curves
![]() $S_{tq}$
,
$S_{tq}$
,
![]() $t\in \mathbb R^+$
. The restriction of
$t\in \mathbb R^+$
. The restriction of
![]() $\overline{\Xi }$
gives a map
$\overline{\Xi }$
gives a map
![]() $\overline{\Xi }_{q^+}:\overline{\mathcal{M}}_{{\rm Dol},q^+}\to \overline{\mathcal{M}}_{{\rm Hit},q^+}$
. We shall study the continuous behavior of
$\overline{\Xi }_{q^+}:\overline{\mathcal{M}}_{{\rm Dol},q^+}\to \overline{\mathcal{M}}_{{\rm Hit},q^+}$
. We shall study the continuous behavior of
![]() $\overline{\Xi }_{q^+}$
for points in the fibre
$\overline{\Xi }_{q^+}$
for points in the fibre
![]() $\mathcal{H}^{-1}(tq)$
as
$\mathcal{H}^{-1}(tq)$
as
![]() $t\to +\infty$
. For convenience, we set
$t\to +\infty$
. For convenience, we set
![]() $\mathcal{M}_{q^+}:=\overline{\mathcal{M}}_{{\rm Dol},q^+}\cap \mathcal{M}_{{\rm Dol}}$
. When
$\mathcal{M}_{q^+}:=\overline{\mathcal{M}}_{{\rm Dol},q^+}\cap \mathcal{M}_{{\rm Dol}}$
. When
![]() $q$
is irreducible, (that is, not a square), all elements in
$q$
is irreducible, (that is, not a square), all elements in
![]() $\mathcal{M}_{q^+}$
are stable. Via the Hitchin [Reference HitchinHit87b] and Beauville–Narasimhan–Ramanan (BNR) correspondence [Reference Narasimhan and RamananBNR89], this reduces the description of the fibre
$\mathcal{M}_{q^+}$
are stable. Via the Hitchin [Reference HitchinHit87b] and Beauville–Narasimhan–Ramanan (BNR) correspondence [Reference Narasimhan and RamananBNR89], this reduces the description of the fibre
![]() $\mathcal{M}_q:=\mathcal{H}^{-1}(q)$
to the characterisation of rank
$\mathcal{M}_q:=\mathcal{H}^{-1}(q)$
to the characterisation of rank
![]() $1$
torsion-free sheaves on the integral curve
$1$
torsion-free sheaves on the integral curve
![]() $S_q$
.
$S_q$
.
In [Reference RegoReg80], parameter spaces for rank
![]() $1$
torsion-free sheaves on algebraic curves with Gorenstein singularities were studied in the context of compactified Jacobians, and the crucial notion of a parabolic module was introduced. This was extensively investigated by Cook in [Reference CookCoo93, Reference CookCoo98], partially following ideas of Bhosle [Reference BhosleBho92]. For simple plane curve singularities of the type appearing in spectral curves, one makes use of the local classification of torsion-free modules of Greuel–Knörrer [Reference Greuel and KnörrerGK85]. These methods were applied to study the Hitchin fibration by Gothen–Oliveira in [Reference Gothen and OliveiraGO13] (see also [Reference Kydonakis, Sun and ZhaoKSZ22] for a recent study). In parallel, Horn [Reference HornHor22a] defines a stratification
$1$
torsion-free sheaves on algebraic curves with Gorenstein singularities were studied in the context of compactified Jacobians, and the crucial notion of a parabolic module was introduced. This was extensively investigated by Cook in [Reference CookCoo93, Reference CookCoo98], partially following ideas of Bhosle [Reference BhosleBho92]. For simple plane curve singularities of the type appearing in spectral curves, one makes use of the local classification of torsion-free modules of Greuel–Knörrer [Reference Greuel and KnörrerGK85]. These methods were applied to study the Hitchin fibration by Gothen–Oliveira in [Reference Gothen and OliveiraGO13] (see also [Reference Kydonakis, Sun and ZhaoKSZ22] for a recent study). In parallel, Horn [Reference HornHor22a] defines a stratification
![]() $\mathcal{M}_q=\bigcup _D\mathcal{M}_{q,D}$
labelled by certain effective divisors contained in the divisor of
$\mathcal{M}_q=\bigcup _D\mathcal{M}_{q,D}$
labelled by certain effective divisors contained in the divisor of
![]() $q$
called
$q$
called
![]() $\sigma$
-divisors (see Section 5.5, and also [Reference Horn and NaHN] for the more general situation).
$\sigma$
-divisors (see Section 5.5, and also [Reference Horn and NaHN] for the more general situation).
Using the results from these references, we reinterpret the work of Mochizuki [Reference MochizukiMoc16] and Mochizuki–Szabó [Reference Mochizuki and SzabóMS23]. We first prove that the restriction of the compactified Kobayashi–Hitchin map to the boundary is discontinuous in general. Following that, by utilising the exponential decay results from Mochizuki–Szabó [Reference Mochizuki and SzabóMS23], which play an essential role, we demonstrate that the entirety of
![]() $\overline{\Xi }_{q^+}$
is discontinuous.
$\overline{\Xi }_{q^+}$
is discontinuous.
Theorem 1.2.
Let
![]() $q\neq 0$
be an irreducible quadratic differential.
$q\neq 0$
be an irreducible quadratic differential.
-
(i) The boundary map
 $\partial \overline{\Xi }_{q^+}|_{\partial \overline{\mathcal{M}}_{{\rm Dol},q^+}^{{\rm st}}}$
is continuous if
$\partial \overline{\Xi }_{q^+}|_{\partial \overline{\mathcal{M}}_{{\rm Dol},q^+}^{{\rm st}}}$
is continuous if
 $q$
has zeros only of odd order and is discontinuous if
$q$
has zeros only of odd order and is discontinuous if
 $q$
has at least one zero of even order.
$q$
has at least one zero of even order.
-
(ii) If
 $q$
has at least one zero of even order, then for each
$q$
has at least one zero of even order, then for each
 $\sigma$
-divisor
$\sigma$
-divisor
 $D\neq 0$
, there exists an even integer
$D\neq 0$
, there exists an even integer
 $n_D\geq 1$
so that for any Higgs bundle
$n_D\geq 1$
so that for any Higgs bundle
 $(\mathcal{F},\psi )\in \mathcal{M}_{q,D}$
, there exist
$(\mathcal{F},\psi )\in \mathcal{M}_{q,D}$
, there exist
 $2n_D$
sequences of Higgs bundles
$2n_D$
sequences of Higgs bundles
 $(\mathcal{E}_i^k,\varphi _i^k)$
,
$(\mathcal{E}_i^k,\varphi _i^k)$
,
 $k=1,\ldots, 2n_D$
such that
$k=1,\ldots, 2n_D$
such that
-
–
 $\lim _{i\to \infty }(\mathcal{E}_i^k,\varphi _i^k)=(\mathcal{F},\psi )$
for
$\lim _{i\to \infty }(\mathcal{E}_i^k,\varphi _i^k)=(\mathcal{F},\psi )$
for
 $k=1,\ldots, 2n_D$
,
$k=1,\ldots, 2n_D$
, -
– and if we write
 \begin{align*}\eta ^k:=\lim _{i\to \infty }\partial \overline {\Xi }_{q^+}\big(\mathcal {E}_i^k,t_i\varphi _i^k\big)\quad,\quad \xi :=\lim _{i\to \infty }\partial \overline {\Xi }_{q^+}(\mathcal {F},t_i\psi )\,\end{align*}
\begin{align*}\eta ^k:=\lim _{i\to \infty }\partial \overline {\Xi }_{q^+}\big(\mathcal {E}_i^k,t_i\varphi _i^k\big)\quad,\quad \xi :=\lim _{i\to \infty }\partial \overline {\Xi }_{q^+}(\mathcal {F},t_i\psi )\,\end{align*}
-
* and if
 $(\mathcal{F},\psi )$
doesn’t lie in the real locus, then
$(\mathcal{F},\psi )$
doesn’t lie in the real locus, then
 $\xi,\eta^1,\ldots,\eta ^{2n_D}$
are
$\xi,\eta^1,\ldots,\eta ^{2n_D}$
are
 $2n_D+1$
different limiting configurations;
$2n_D+1$
different limiting configurations;
-
* if
 $(\mathcal{F},\psi )$
lies in the real locus, then
$(\mathcal{F},\psi )$
lies in the real locus, then
 $\eta ^i\cong \eta ^{n_D+i}$
for
$\eta ^i\cong \eta ^{n_D+i}$
for
 $i=1,\cdots, n$
, and we obtain
$i=1,\cdots, n$
, and we obtain
 $n_D+1$
different limiting configurations.
$n_D+1$
different limiting configurations.
-
-
– for each
 $k$
, there exist constants
$k$
, there exist constants
 $t_i\to +\infty$
such that
$t_i\to +\infty$
such that
 $\lim _{i\to \infty }\overline{\Xi }_{q^+}(\mathcal{E}_i^k,t_i\varphi _i^k)\neq \overline{\Xi }_{q^+}(\mathcal{F},\psi )$
.
$\lim _{i\to \infty }\overline{\Xi }_{q^+}(\mathcal{E}_i^k,t_i\varphi _i^k)\neq \overline{\Xi }_{q^+}(\mathcal{F},\psi )$
.
-
When
![]() $q$
is reducible, the description of Higgs bundles in the fibre over
$q$
is reducible, the description of Higgs bundles in the fibre over
![]() $q$
becomes more complicated because of, among other things, the existence of strictly semistable objects. To understand this, we use the local descriptions of Gothen–Oliveira and Mochizuki (see [Reference Gothen and OliveiraGO13, Reference MochizukiMoc16]). In contrast to the irreducible case, the analogous exponential decay result to that of Mochizuki–Szabó [Reference MochizukiMoc16] is, unfortunately, currently not available. This results in a weaker statement for the reducible fibre. Recall that we have defined
$q$
becomes more complicated because of, among other things, the existence of strictly semistable objects. To understand this, we use the local descriptions of Gothen–Oliveira and Mochizuki (see [Reference Gothen and OliveiraGO13, Reference MochizukiMoc16]). In contrast to the irreducible case, the analogous exponential decay result to that of Mochizuki–Szabó [Reference MochizukiMoc16] is, unfortunately, currently not available. This results in a weaker statement for the reducible fibre. Recall that we have defined
![]() $\overline{\Xi }_{q^+}:\overline{\mathcal{M}}_{{\rm Dol},q^+}\to \overline{\mathcal{M}}_{{\rm Hit},q^+}$
as the compactified Kobayashi–Hitchin map and
$\overline{\Xi }_{q^+}:\overline{\mathcal{M}}_{{\rm Dol},q^+}\to \overline{\mathcal{M}}_{{\rm Hit},q^+}$
as the compactified Kobayashi–Hitchin map and
![]() $\partial \overline{\Xi }_{q^+}:\partial \overline{\mathcal{M}}_{{\rm Dol},q^+}\to \partial \overline{\mathcal{M}}_{{\rm Hit},q^+}$
as its restriction to the compactified boundary. With this notation, the following holds:
$\partial \overline{\Xi }_{q^+}:\partial \overline{\mathcal{M}}_{{\rm Dol},q^+}\to \partial \overline{\mathcal{M}}_{{\rm Hit},q^+}$
as its restriction to the compactified boundary. With this notation, the following holds:
Theorem 1.3.
Suppose that
![]() $q\neq 0$
is reducible; if
$q\neq 0$
is reducible; if
![]() $g\geq 3$
, then the boundary map
$g\geq 3$
, then the boundary map
![]() $\partial \overline{\Xi }_{q^+}|_{\partial \overline{\mathcal{M}}_{{\rm Dol},q^+}^{{\rm st}}}$
is discontinuous. However, if
$\partial \overline{\Xi }_{q^+}|_{\partial \overline{\mathcal{M}}_{{\rm Dol},q^+}^{{\rm st}}}$
is discontinuous. However, if
![]() $g=2$
, the boundary map
$g=2$
, the boundary map
![]() $\partial \overline{\Xi }_{q^+}|_{\partial \overline{\mathcal{M}}_{{\rm Dol},q^+}^{{\rm st}}}$
is continuous.
$\partial \overline{\Xi }_{q^+}|_{\partial \overline{\mathcal{M}}_{{\rm Dol},q^+}^{{\rm st}}}$
is continuous.
This article is organized as follows: In Section 2, we provide a brief overview of Higgs bundles and the BNR correspondence. In Section 3, we introduce the concepts of filtered bundles and their compactness properties. Section 4 defines the algebraic and analytic compactifications. Section 5 introduces parabolic modules and examines their connection to spectral curves. The main results for Hitchin fibres with irreducible singular spectral curves are established in Section 6. In Section 7, the results for the reducible case are proven. Finally, in Section 8, we construct the compactified Kobayashi–Hitchin map and prove the main results. The Appendix, based on the work of Greuel–Knörrer, calculates some invariants of rank
![]() $1$
torsion-free sheaves on the spectral curves we consider.
$1$
torsion-free sheaves on the spectral curves we consider.
2. Background on Higgs bundles
This section gives a very brief overview of the Dolbeault and Hitchin moduli spaces, spectral curve descriptions and the nonabelian Hodge correspondence. For more details on these topics, see [Reference HitchinHit87a, Reference HitchinHit87b, Reference SimpsonSim92].
2.1 Higgs bundles
As in the Introduction, throughout this paper
![]() $\Sigma$
will denote a closed Riemann surface of genus
$\Sigma$
will denote a closed Riemann surface of genus
![]() $g\geq 2$
, with structure sheaf
$g\geq 2$
, with structure sheaf
![]() $\mathcal{O}=\mathcal{O}_\Sigma$
and canonical bundle
$\mathcal{O}=\mathcal{O}_\Sigma$
and canonical bundle
![]() $K=K_\Sigma$
. Let
$K=K_\Sigma$
. Let
![]() $E\to \Sigma$
be a complex vector bundle. A Higgs bundle consists of a pair
$E\to \Sigma$
be a complex vector bundle. A Higgs bundle consists of a pair
![]() $(\mathcal{E},\varphi )$
, where
$(\mathcal{E},\varphi )$
, where
![]() $\mathcal{E}$
is a holomorphic bundle structure on
$\mathcal{E}$
is a holomorphic bundle structure on
![]() $E$
and where
$E$
and where
![]() $\varphi \in H^0 ({\rm End}(\mathcal{E})\otimes K)$
. If
$\varphi \in H^0 ({\rm End}(\mathcal{E})\otimes K)$
. If
![]() ${\rm rank}(E)=1$
, then a Higgs field is just an abelian differential
${\rm rank}(E)=1$
, then a Higgs field is just an abelian differential
![]() $\omega$
. The pair
$\omega$
. The pair
![]() $(\mathcal{E},\varphi )$
is called an
$(\mathcal{E},\varphi )$
is called an
![]() ${\rm SL}(2,\mathbb{C})$
Higgs bundle if
${\rm SL}(2,\mathbb{C})$
Higgs bundle if
![]() ${\rm rank}(E)=2$
,
${\rm rank}(E)=2$
,
![]() $\det (\mathcal{E})$
has a fixed isomorphism with the trivial bundle and if
$\det (\mathcal{E})$
has a fixed isomorphism with the trivial bundle and if
![]() ${\rm Tr}(\varphi )=0$
. In this article we will focus mainly on
${\rm Tr}(\varphi )=0$
. In this article we will focus mainly on
![]() ${\rm SL}(2,\mathbb{C})$
Higgs bundles, but the rank
${\rm SL}(2,\mathbb{C})$
Higgs bundles, but the rank
![]() $1$
case will also be important.
$1$
case will also be important.
Let
![]() $(\mathcal{E},\varphi )$
be an
$(\mathcal{E},\varphi )$
be an
![]() ${\rm SL}(2,\mathbb{C})$
Higgs bundle. A (proper) Higgs subbundle of
${\rm SL}(2,\mathbb{C})$
Higgs bundle. A (proper) Higgs subbundle of
![]() $(\mathcal{E},\varphi )$
is a holomorphic line bundle
$(\mathcal{E},\varphi )$
is a holomorphic line bundle
![]() $\mathcal{L}\subset \mathcal{E}$
that is
$\mathcal{L}\subset \mathcal{E}$
that is
![]() $\varphi$
-invariant; that is,
$\varphi$
-invariant; that is,
![]() $\varphi :\mathcal{L}\to \mathcal{L}\otimes K$
. In this case the restriction
$\varphi :\mathcal{L}\to \mathcal{L}\otimes K$
. In this case the restriction
![]() $\varphi _{\mathcal{L}}:=\varphi \bigr |_{\mathcal L}$
makes
$\varphi _{\mathcal{L}}:=\varphi \bigr |_{\mathcal L}$
makes
![]() $(\mathcal{L},\varphi _{\mathcal{L}})$
a rank
$(\mathcal{L},\varphi _{\mathcal{L}})$
a rank
![]() $1$
Higgs bundle. Moreover,
$1$
Higgs bundle. Moreover,
![]() $\varphi$
induces a Higgs bundle structure on the quotient
$\varphi$
induces a Higgs bundle structure on the quotient
![]() $\mathcal{E}/\mathcal{L}$
. We say that
$\mathcal{E}/\mathcal{L}$
. We say that
![]() $(\mathcal{E},\varphi )$
is stable (resp. semistable) if for all Higgs subbundles
$(\mathcal{E},\varphi )$
is stable (resp. semistable) if for all Higgs subbundles
![]() $\mathcal{L}$
,
$\mathcal{L}$
,
![]() $\deg \mathcal{L}\lt 0$
(resp.
$\deg \mathcal{L}\lt 0$
(resp.
![]() $\deg \mathcal{L}\leq 0$
). We say that
$\deg \mathcal{L}\leq 0$
). We say that
![]() $(\mathcal{E},\varphi )$
is polystable if
$(\mathcal{E},\varphi )$
is polystable if
![]() $(\mathcal{E},\varphi )\simeq (\mathcal{L},\omega )\oplus (\mathcal{L}^{-1},-\omega )$
, where
$(\mathcal{E},\varphi )\simeq (\mathcal{L},\omega )\oplus (\mathcal{L}^{-1},-\omega )$
, where
![]() $\mathcal{L}$
is a degree-zero holomorphic line bundle and
$\mathcal{L}$
is a degree-zero holomorphic line bundle and
![]() $\omega \in H^0(K)$
.
$\omega \in H^0(K)$
.
If
![]() $(\mathcal{E},\varphi )$
is strictly semistable (that is, semistable but not polystable), the Seshadri filtration [Reference SeshadriSes67] gives the unique Higgs subbundle
$(\mathcal{E},\varphi )$
is strictly semistable (that is, semistable but not polystable), the Seshadri filtration [Reference SeshadriSes67] gives the unique Higgs subbundle
![]() $0\subset (\mathcal{L},\omega )\subset (\mathcal{E},\varphi )$
, with
$0\subset (\mathcal{L},\omega )\subset (\mathcal{E},\varphi )$
, with
![]() $\deg (\mathcal{L})={1 \over 2}\deg (\mathcal{E})=0$
. If we write
$\deg (\mathcal{L})={1 \over 2}\deg (\mathcal{E})=0$
. If we write
![]() $(\mathcal{L}^{\prime},\omega ^{\prime}):=(\mathcal{E},\varphi )/(\mathcal{L},\omega )$
, then we have
$(\mathcal{L}^{\prime},\omega ^{\prime}):=(\mathcal{E},\varphi )/(\mathcal{L},\omega )$
, then we have
![]() $\omega ^{\prime}=-\omega$
and
$\omega ^{\prime}=-\omega$
and
![]() $\mathcal{L}^{\prime}=\mathcal{L}^{-1}$
. The associated graded bundle
$\mathcal{L}^{\prime}=\mathcal{L}^{-1}$
. The associated graded bundle
![]() ${\rm Gr}(\mathcal{E},\varphi )=(\mathcal{L},\omega )\oplus (\mathcal{L}^{-1},-\omega )$
of this filtration is a polystable
${\rm Gr}(\mathcal{E},\varphi )=(\mathcal{L},\omega )\oplus (\mathcal{L}^{-1},-\omega )$
of this filtration is a polystable
![]() ${\rm SL}(2,\mathbb{C})$
Higgs bundle. We say that
${\rm SL}(2,\mathbb{C})$
Higgs bundle. We say that
![]() $(\mathcal{E},\varphi )$
is S-equivalent to
$(\mathcal{E},\varphi )$
is S-equivalent to
![]() ${\rm Gr}(\mathcal{E},\varphi )$
.
${\rm Gr}(\mathcal{E},\varphi )$
.
Holomorphic bundles
![]() $\mathcal{E}$
, with underlying
$\mathcal{E}$
, with underlying
![]() $C^\infty$
bundle
$C^\infty$
bundle
![]() $E$
, are in 1-to-1 correspondence, with
$E$
, are in 1-to-1 correspondence, with
![]() $\bar \partial$
-operators
$\bar \partial$
-operators
![]() $\bar \partial _E: \Omega^0(E)\to \Omega ^{0,1}(E)$
. We use the notation
$\bar \partial _E: \Omega^0(E)\to \Omega ^{0,1}(E)$
. We use the notation
![]() $\mathcal{E}:=(E,\bar{\partial }_E)$
. Let
$\mathcal{E}:=(E,\bar{\partial }_E)$
. Let
![]() $\mathcal{C}$
denote the space of pairs
$\mathcal{C}$
denote the space of pairs
![]() $ (\bar \partial _E,\varphi )$
,
$ (\bar \partial _E,\varphi )$
,
![]() $\bar \partial _E\varphi=0$
. Let
$\bar \partial _E\varphi=0$
. Let
![]() $\mathcal{C}^s$
and
$\mathcal{C}^s$
and
![]() $\mathcal{C}^{ss}$
denote the subspaces of
$\mathcal{C}^{ss}$
denote the subspaces of
![]() $\mathcal{C}$
where the Higgs bundles are stable (resp. semistable). The complex gauge transformation group
$\mathcal{C}$
where the Higgs bundles are stable (resp. semistable). The complex gauge transformation group
![]() $\mathcal{G}_{\mathbb{C}}:={\rm Aut}(E)$
has a right-hand action on
$\mathcal{G}_{\mathbb{C}}:={\rm Aut}(E)$
has a right-hand action on
![]() $\mathcal{C}$
by defining for
$\mathcal{C}$
by defining for
![]() $g\in \mathcal{G}_{\mathbb{C}}$
,
$g\in \mathcal{G}_{\mathbb{C}}$
,
![]() $(\bar{\partial }_E,\varphi )g:=(g^{-1}\circ \bar{\partial }\circ g,g^{-1}\circ \varphi \circ g)$
.
$(\bar{\partial }_E,\varphi )g:=(g^{-1}\circ \bar{\partial }\circ g,g^{-1}\circ \varphi \circ g)$
.
There is a quasiprojective scheme
![]() $\mathcal{M}_{{\rm Dol}}$
whose closed points are in 1-to-1 correspondence with isomorphism classes of polystable
$\mathcal{M}_{{\rm Dol}}$
whose closed points are in 1-to-1 correspondence with isomorphism classes of polystable
![]() ${\rm SL}(2,\mathbb{C})$
Higgs bundles constructed via (finite dimensional) Geometric Invariant Theory (see [Reference NitsureNit91, Reference SimpsonSim94]). In [Reference FanFan22b] it was shown that the infinite dimensional quotient
${\rm SL}(2,\mathbb{C})$
Higgs bundles constructed via (finite dimensional) Geometric Invariant Theory (see [Reference NitsureNit91, Reference SimpsonSim94]). In [Reference FanFan22b] it was shown that the infinite dimensional quotient
![]() $\mathcal{C}^{{\rm ss}}//\mathcal{G}_{\mathbb{C}}$
, where the double slash indicates that S-equivalent orbits are identified, admits the structure of a complex analytic space that is biholomorphic to the analytification
$\mathcal{C}^{{\rm ss}}//\mathcal{G}_{\mathbb{C}}$
, where the double slash indicates that S-equivalent orbits are identified, admits the structure of a complex analytic space that is biholomorphic to the analytification
![]() $\mathcal{M}_{{\rm Dol}}^{\textrm{an}}$
of
$\mathcal{M}_{{\rm Dol}}^{\textrm{an}}$
of
![]() $\mathcal{M}_{{\rm Dol}}$
. Henceforth, we shall work in the complex analytic category; identify the algebro–geometric and gauge theoretic moduli spaces as complex analytic spaces; and simply denote them both by
$\mathcal{M}_{{\rm Dol}}$
. Henceforth, we shall work in the complex analytic category; identify the algebro–geometric and gauge theoretic moduli spaces as complex analytic spaces; and simply denote them both by
![]() $\mathcal{M}_{{\rm Dol}}$
. We note that the set of stable Higgs bundles modulo gauge transformations,
$\mathcal{M}_{{\rm Dol}}$
. We note that the set of stable Higgs bundles modulo gauge transformations,
![]() $\mathcal{M}_{{\rm Dol}}^s:=\mathcal{C}^{{\rm s}}/\mathcal{G}_{\mathbb{C}}$
, is a geometric quotient and an open subset of
$\mathcal{M}_{{\rm Dol}}^s:=\mathcal{C}^{{\rm s}}/\mathcal{G}_{\mathbb{C}}$
, is a geometric quotient and an open subset of
![]() $\mathcal{M}_{{\rm Dol}}$
.
$\mathcal{M}_{{\rm Dol}}$
.
Finally, notice that the pair
![]() $(\mathcal{E},\varphi )$
is stable (resp. semistable) if and only if the same is true for
$(\mathcal{E},\varphi )$
is stable (resp. semistable) if and only if the same is true for
![]() $(\mathcal{E},\lambda \varphi )$
,
$(\mathcal{E},\lambda \varphi )$
,
![]() $\lambda \in \mathbb{C}^\ast$
. Hence,
$\lambda \in \mathbb{C}^\ast$
. Hence,
![]() $\mathcal{M}_{{\rm Dol}}$
admits an action of
$\mathcal{M}_{{\rm Dol}}$
admits an action of
![]() $\mathbb{C}^\ast$
that preserves
$\mathbb{C}^\ast$
that preserves
![]() $\mathcal{M}_{{\rm Dol}}^{s}$
. Although
$\mathcal{M}_{{\rm Dol}}^{s}$
. Although
![]() $\mathcal{M}_{{\rm Dol}}$
is only quasiprojective, the
$\mathcal{M}_{{\rm Dol}}$
is only quasiprojective, the
![]() $\mathbb{C}^\ast$
action satisfies the Białynicki–Birula property:
$\mathbb{C}^\ast$
action satisfies the Białynicki–Birula property:
Theorem 2.1.
For any
![]() $[(\mathcal{E},\varphi )]\in \mathcal{M}_{{\rm Dol}}$
,
$[(\mathcal{E},\varphi )]\in \mathcal{M}_{{\rm Dol}}$
,
exists in
![]() $\mathcal{M}_{{\rm Dol}}$
.
$\mathcal{M}_{{\rm Dol}}$
.
2.2 Spectral curves and the Hitchin fibration
The Hitchin map is defined as
where
![]() $H^0(K^2)=:\mathcal{B}$
is known as the Hitchin base. Hitchin [Reference HitchinHit87a, Reference HitchinHit87b] showed that
$H^0(K^2)=:\mathcal{B}$
is known as the Hitchin base. Hitchin [Reference HitchinHit87a, Reference HitchinHit87b] showed that
![]() $\mathcal{H}$
is a proper map and a fibration by abelian varieties over the open cone
$\mathcal{H}$
is a proper map and a fibration by abelian varieties over the open cone
![]() $\mathcal{B}^{\textrm{reg}}\subset \mathcal{B}$
consisting of nonzero quadratic differentials with only simple zeros. The discriminant locus
$\mathcal{B}^{\textrm{reg}}\subset \mathcal{B}$
consisting of nonzero quadratic differentials with only simple zeros. The discriminant locus
![]() $\mathcal{B}^{\textrm{sing}}:=\mathcal{B}\setminus \mathcal{B}^{\textrm{reg}}$
consists of quadratic differentials that either are identically zero or have at least one zero with multiplicity. For
$\mathcal{B}^{\textrm{sing}}:=\mathcal{B}\setminus \mathcal{B}^{\textrm{reg}}$
consists of quadratic differentials that either are identically zero or have at least one zero with multiplicity. For
![]() $q\in \mathcal{B}$
, let
$q\in \mathcal{B}$
, let
![]() $\mathcal{M}_q:=\mathcal{H}^{-1}(q)$
. The ‘most singular fibre’
$\mathcal{M}_q:=\mathcal{H}^{-1}(q)$
. The ‘most singular fibre’
![]() $\mathcal{M}_0$
is called the nilpotent cone.
$\mathcal{M}_0$
is called the nilpotent cone.
Consider the total space
![]() ${\rm Tot}(K)$
of
${\rm Tot}(K)$
of
![]() $K$
, along with its projection
$K$
, along with its projection
![]() $\pi : {\rm Tot}(K) \to \Sigma$
. The pull-back bundle
$\pi : {\rm Tot}(K) \to \Sigma$
. The pull-back bundle
![]() $\pi ^* K$
has a tautological section, which we denote by
$\pi ^* K$
has a tautological section, which we denote by
![]() $\lambda \in H^0({\rm Tot}(K),\pi ^\ast K)$
. Given any
$\lambda \in H^0({\rm Tot}(K),\pi ^\ast K)$
. Given any
![]() $q\neq 0 \in H^0(K^2)$
, the spectral curve
$q\neq 0 \in H^0(K^2)$
, the spectral curve
![]() $S_q$
associated with
$S_q$
associated with
![]() $q$
is the zero scheme of the section
$q$
is the zero scheme of the section
![]() $\lambda^2 - \pi ^\ast q \in H^0({\rm Tot}(K),\pi ^* K)$
. This is a reduced, but possibly reducible, projective algebraic curve. The restriction of
$\lambda^2 - \pi ^\ast q \in H^0({\rm Tot}(K),\pi ^* K)$
. This is a reduced, but possibly reducible, projective algebraic curve. The restriction of
![]() $\pi$
to
$\pi$
to
![]() $S_q$
, also denoted by
$S_q$
, also denoted by
![]() $\pi : S_q \to \Sigma$
, is a double covering branched along the zeros of
$\pi : S_q \to \Sigma$
, is a double covering branched along the zeros of
![]() $q$
.
$q$
.
The spectral curve
![]() $S_q$
is smooth if and only if
$S_q$
is smooth if and only if
![]() $q$
has only simple zeros. It is reducible if and only if
$q$
has only simple zeros. It is reducible if and only if
![]() $q = -\omega \otimes \omega$
for some
$q = -\omega \otimes \omega$
for some
![]() $\omega \in H^0(K)$
. In the latter case, we call such quadratic differentials reducible, and we otherwise refer to them as irreducible. There is a noteworthy observation regarding irreducible spectral curves.
$\omega \in H^0(K)$
. In the latter case, we call such quadratic differentials reducible, and we otherwise refer to them as irreducible. There is a noteworthy observation regarding irreducible spectral curves.
Proposition 2.2.
Let
![]() $(\mathcal{E},\varphi )$
be a Higgs bundle with
$(\mathcal{E},\varphi )$
be a Higgs bundle with
![]() $q = \det (\varphi )$
, and suppose that
$q = \det (\varphi )$
, and suppose that
![]() $q$
is irreducible. Then
$q$
is irreducible. Then
![]() $(\mathcal{E},\varphi )$
has no proper invariant subbundles. In particular,
$(\mathcal{E},\varphi )$
has no proper invariant subbundles. In particular,
![]() $(\mathcal{E},\varphi )$
is stable.
$(\mathcal{E},\varphi )$
is stable.
Proof.
Suppose
![]() $\mathcal{L}\subset \mathcal{E}$
is
$\mathcal{L}\subset \mathcal{E}$
is
![]() $\varphi$
-invariant, and let
$\varphi$
-invariant, and let
![]() $\varphi _{\mathcal L}$
be the restriction. Then
$\varphi _{\mathcal L}$
be the restriction. Then
which contradicts the assumption.
Let us emphasise that being reducible is not the same as having only even zeros. To see this, suppose that
![]() ${\rm Div}(q)=2D$
. Then
${\rm Div}(q)=2D$
. Then
![]() $K\simeq \mathcal{O}(D)\otimes \mathcal{I}$
, where
$K\simeq \mathcal{O}(D)\otimes \mathcal{I}$
, where
![]() $\mathcal{I}$
is a 2-torsion point in the Jacobian. The spectral curve
$\mathcal{I}$
is a 2-torsion point in the Jacobian. The spectral curve
![]() $S_q$
is reducible if and only if
$S_q$
is reducible if and only if
![]() $\mathcal{I}$
is trivial.
$\mathcal{I}$
is trivial.
2.3 Rank 1 torsion-free sheaves and the BNR correspondence
In this subsection, we provide some background on rank 1 torsion-free sheaf theory over spectral curves in the context of the Hitchin and BNR correspondence, as developed in [Reference HitchinHit87b, Reference Narasimhan and RamananBNR89].
Let
![]() $S$
be a reduced and irreducible complex projective curve and
$S$
be a reduced and irreducible complex projective curve and
![]() $\mathcal{O}_S$
its structure sheaf. The moduli space of invertible sheaves on
$\mathcal{O}_S$
its structure sheaf. The moduli space of invertible sheaves on
![]() $S$
is denoted by
$S$
is denoted by
![]() ${\rm Pic}(S)$
. If
${\rm Pic}(S)$
. If
![]() $\mathcal F$
is a coherent analytic sheaf on
$\mathcal F$
is a coherent analytic sheaf on
![]() $S$
, we can define its cohomology groups
$S$
, we can define its cohomology groups
![]() $H^i(S,\mathcal{F})$
. Since
$H^i(S,\mathcal{F})$
. Since
![]() $\dim S=1$
,
$\dim S=1$
,
![]() $H^i(S,\mathcal{F})=0$
for
$H^i(S,\mathcal{F})=0$
for
![]() $i\geq 2$
. The Euler characteristic is defined as
$i\geq 2$
. The Euler characteristic is defined as
![]() $\chi (\mathcal{F})=\dim H^0(S,\mathcal{F})-\dim H^1(S,\mathcal{F})$
. The degree of a torsion-free sheaf
$\chi (\mathcal{F})=\dim H^0(S,\mathcal{F})-\dim H^1(S,\mathcal{F})$
. The degree of a torsion-free sheaf
![]() $\mathcal{F}$
is given by
$\mathcal{F}$
is given by
![]() $\deg (\mathcal{F})=\chi (\mathcal{F})-{\rm rank}(\mathcal{F})\chi (\mathcal{O}_S)$
. If
$\deg (\mathcal{F})=\chi (\mathcal{F})-{\rm rank}(\mathcal{F})\chi (\mathcal{O}_S)$
. If
![]() $\mathcal{F}$
is locally free, then
$\mathcal{F}$
is locally free, then
![]() $\deg (\mathcal{F})$
coincides with the degree of the invertible sheaf
$\deg (\mathcal{F})$
coincides with the degree of the invertible sheaf
![]() $\det (\mathcal{F})$
. We let
$\det (\mathcal{F})$
. We let
![]() ${\rm Pic}^d(S)\subset {\rm Pic}(S)$
denote the degree
${\rm Pic}^d(S)\subset {\rm Pic}(S)$
denote the degree
![]() $d$
component.
$d$
component.
Let
![]() $\overline{{\rm Pic}}^d(S)$
be the moduli space of degree
$\overline{{\rm Pic}}^d(S)$
be the moduli space of degree
![]() $d$
, rank 1 torsion-free sheaves on
$d$
, rank 1 torsion-free sheaves on
![]() $S$
, and let
$S$
, and let
![]() $\overline{{\rm Pic}}(S)=\prod _{d\in \mathbb{Z}}\overline{{\rm Pic}}^d(S)$
[D’S79]. Then,
$\overline{{\rm Pic}}(S)=\prod _{d\in \mathbb{Z}}\overline{{\rm Pic}}^d(S)$
[D’S79]. Then,
![]() $\overline{{\rm Pic}}^d(S)$
is an irreducible projective scheme containing
$\overline{{\rm Pic}}^d(S)$
is an irreducible projective scheme containing
![]() ${\rm Pic}^d(S)$
as an open subscheme. When
${\rm Pic}^d(S)$
as an open subscheme. When
![]() $S$
is smooth, we have
$S$
is smooth, we have
![]() $\overline{{\rm Pic}}^d(S)={\rm Pic}^d(S)$
. The relationship to Higgs bundles is given by the following:
$\overline{{\rm Pic}}^d(S)={\rm Pic}^d(S)$
. The relationship to Higgs bundles is given by the following:
Theorem 2.3.
Let
![]() $q\in H^0(K^2)$
be an irreducible quadratic differential with spectral curve
$q\in H^0(K^2)$
be an irreducible quadratic differential with spectral curve
![]() $S_q$
. There is then a bijective correspondence between points in
$S_q$
. There is then a bijective correspondence between points in
![]() $\overline{{\rm Pic}}(S_q)$
and isomorphism classes of rank 2 Higgs pairs
$\overline{{\rm Pic}}(S_q)$
and isomorphism classes of rank 2 Higgs pairs
![]() $(\mathcal{E},\varphi )$
with
$(\mathcal{E},\varphi )$
with
![]() ${\rm Tr}(\varphi )=0$
and
${\rm Tr}(\varphi )=0$
and
![]() $\det (\varphi )=q$
. Explicitly: If
$\det (\varphi )=q$
. Explicitly: If
![]() $\mathcal{L}\in \overline{{\rm Pic}}(S_q)$
, then
$\mathcal{L}\in \overline{{\rm Pic}}(S_q)$
, then
![]() $\mathcal{E}:=\pi _{\ast }(\mathcal{L})$
is a rank 2 vector bundle, and the homomorphism
$\mathcal{E}:=\pi _{\ast }(\mathcal{L})$
is a rank 2 vector bundle, and the homomorphism
![]() $\pi _{\ast }\mathcal{L}\to \pi _{\ast }\mathcal{L}\otimes K\cong \pi _{\ast }(\mathcal{L}\otimes \pi ^{\ast }K)$
, given by multiplication by the canonical section
$\pi _{\ast }\mathcal{L}\to \pi _{\ast }\mathcal{L}\otimes K\cong \pi _{\ast }(\mathcal{L}\otimes \pi ^{\ast }K)$
, given by multiplication by the canonical section
![]() $\lambda$
, defines the Higgs field
$\lambda$
, defines the Higgs field
![]() $\varphi$
.
$\varphi$
.
This correspondence gives the very useful exact sequence
for some ideal sheaf
![]() $\mathcal{I}$
. If
$\mathcal{I}$
. If
![]() $S$
is smooth, then
$S$
is smooth, then
![]() $\mathcal{I}=\mathcal{O}_S(-\Delta )$
, where
$\mathcal{I}=\mathcal{O}_S(-\Delta )$
, where
![]() $\Delta$
is the ramification divisor. The sequence (3) will be used in Section 6.
$\Delta$
is the ramification divisor. The sequence (3) will be used in Section 6.
Let
![]() $q$
be a quadratic differential with only simple zeros, and to simplify notation, write
$q$
be a quadratic differential with only simple zeros, and to simplify notation, write
![]() $S=S_q$
. Let
$S=S_q$
. Let
![]() $\Lambda :={\rm Div}(\lambda )$
be the ramification divisor of the map
$\Lambda :={\rm Div}(\lambda )$
be the ramification divisor of the map
![]() $\pi :S\to \Sigma$
. By the Riemann–Hurwitz formula, the genus of
$\pi :S\to \Sigma$
. By the Riemann–Hurwitz formula, the genus of
![]() $S$
is
$S$
is
![]() $g(S)=4g-3$
, where
$g(S)=4g-3$
, where
![]() $g$
is the genus of
$g$
is the genus of
![]() $\Sigma$
. Furthermore, for any
$\Sigma$
. Furthermore, for any
![]() $\mathcal{L}\in {\rm Pic}(S)$
, Riemann–Roch gives
$\mathcal{L}\in {\rm Pic}(S)$
, Riemann–Roch gives
![]() $\deg (\pi _{\ast }\mathcal{L})=\deg (\mathcal{L})-(2g-2).$
The
$\deg (\pi _{\ast }\mathcal{L})=\deg (\mathcal{L})-(2g-2).$
The
![]() ${\rm SL}(2,\mathbb{C})$
Higgs bundles are characterized by
${\rm SL}(2,\mathbb{C})$
Higgs bundles are characterized by
By the Hitchin–BNR correspondence (Theorem 2.3), the map
![]() $\chi _{{\rm BNR}}:\mathcal{T}\to \mathcal{M}_q$
is a bijection.
$\chi _{{\rm BNR}}:\mathcal{T}\to \mathcal{M}_q$
is a bijection.
The branched double cover
![]() $\pi :S\to \Sigma$
is given by an involution
$\pi :S\to \Sigma$
is given by an involution
![]() $\sigma :S\to S$
. We have the norm map
$\sigma :S\to S$
. We have the norm map
![]() ${\rm Nm}_{S/\Sigma }:{\rm Jac}(S)\to {\rm Jac}(\Sigma )$
, where
${\rm Nm}_{S/\Sigma }:{\rm Jac}(S)\to {\rm Jac}(\Sigma )$
, where
![]() ${\rm Jac}(S)$
is the connected component of the trivial line bundle in
${\rm Jac}(S)$
is the connected component of the trivial line bundle in
![]() ${\rm Pic}(S)$
and
${\rm Pic}(S)$
and
![]() ${\rm Nm}_{S/\Sigma }(\mathcal{O}_{S}(D)):=\mathcal{O}_{\Sigma }(\pi (D))$
. The Prym variety is defined as
${\rm Nm}_{S/\Sigma }(\mathcal{O}_{S}(D)):=\mathcal{O}_{\Sigma }(\pi (D))$
. The Prym variety is defined as
Also, we have
![]() $\det (\pi _{\ast }\mathcal{L})\cong {\rm Nm}_{S/\Sigma }(\mathcal{L})\otimes K^{-1}$
. Thus,
$\det (\pi _{\ast }\mathcal{L})\cong {\rm Nm}_{S/\Sigma }(\mathcal{L})\otimes K^{-1}$
. Thus,
![]() $\mathcal{T}$
can be expressed as
$\mathcal{T}$
can be expressed as
Hence,
![]() $\mathcal{T}$
is a torsor over
$\mathcal{T}$
is a torsor over
![]() ${\rm Prym}(S/\Sigma )$
. Explicitly, by choosing
${\rm Prym}(S/\Sigma )$
. Explicitly, by choosing
![]() $\mathcal{L}_0\in \mathcal{T}$
, we obtain an isomorphism
$\mathcal{L}_0\in \mathcal{T}$
, we obtain an isomorphism
![]() $\mathcal{T}\xrightarrow{\sim } {\rm Prym}(S/\Sigma )$
given by
$\mathcal{T}\xrightarrow{\sim } {\rm Prym}(S/\Sigma )$
given by
![]() $\mathcal{L}\to \mathcal{L}\otimes \mathcal{L}_0^{-1}$
.
$\mathcal{L}\to \mathcal{L}\otimes \mathcal{L}_0^{-1}$
.
To summarize, we have the following:
Proposition 2.4.
Let
![]() $q$
be a quadratic differential with simple zeros. Then
$q$
be a quadratic differential with simple zeros. Then
![]() $\mathcal{M}_q\cong \mathcal{T}\cong {\rm Prym}(S/\Sigma )$
.
$\mathcal{M}_q\cong \mathcal{T}\cong {\rm Prym}(S/\Sigma )$
.
If
![]() $q\neq 0$
is irreducible but nongeneric, the spectral curve
$q\neq 0$
is irreducible but nongeneric, the spectral curve
![]() $S$
is singular and irreducible. We may still define the set
$S$
is singular and irreducible. We may still define the set
![]() $\overline{\mathcal{T}}\subset \overline{{\rm Pic}}^{2g-2}(S)$
as follows:
$\overline{\mathcal{T}}\subset \overline{{\rm Pic}}^{2g-2}(S)$
as follows:
We also set
![]() $\mathcal{T}:=\overline{\mathcal{T}}\cap {\rm Pic}^{2g-2}$
. Then
$\mathcal{T}:=\overline{\mathcal{T}}\cap {\rm Pic}^{2g-2}$
. Then
![]() $\overline{\mathcal{T}}$
is the natural compactification of
$\overline{\mathcal{T}}$
is the natural compactification of
![]() $\mathcal{T}$
induced by the inclusion
$\mathcal{T}$
induced by the inclusion
![]() ${\rm Pic}^{2g-2}(S)\subset \overline{{\rm Pic}}(S)$
. The BNR correspondence, as stated in Theorem 2.3, implies that
${\rm Pic}^{2g-2}(S)\subset \overline{{\rm Pic}}(S)$
. The BNR correspondence, as stated in Theorem 2.3, implies that
![]() $\chi _{{\rm BNR}}:\overline{\mathcal{T}}\to \mathcal{M}_q$
is an isomorphism.
$\chi _{{\rm BNR}}:\overline{\mathcal{T}}\to \mathcal{M}_q$
is an isomorphism.
2.4 The Hitchin moduli space and the nonabelian Hodge correspondence
We now recall the well-known nonabelian Hodge correspondence (NAH), which relates the space of flat
![]() ${\rm SL}(2,\mathbb{C})$
connections, Higgs bundles and solutions to the Hitchin equations. This result was developed in the work of Hitchin [Reference HitchinHit87a], Simpson [Reference SimpsonSim88], Corlette [Reference CorletteCor88] and Donaldson [Reference DonaldsonDon87].
${\rm SL}(2,\mathbb{C})$
connections, Higgs bundles and solutions to the Hitchin equations. This result was developed in the work of Hitchin [Reference HitchinHit87a], Simpson [Reference SimpsonSim88], Corlette [Reference CorletteCor88] and Donaldson [Reference DonaldsonDon87].
As above, let
![]() $E$
be a trivial(ised), smooth, rank 2 vector bundle over the Riemann surface
$E$
be a trivial(ised), smooth, rank 2 vector bundle over the Riemann surface
![]() $\Sigma$
, and let
$\Sigma$
, and let
![]() $H_0$
be a fixed Hermitian metric on
$H_0$
be a fixed Hermitian metric on
![]() $E$
. We denote by
$E$
. We denote by
![]() $\mathfrak{sl}(E)$
(resp.
$\mathfrak{sl}(E)$
(resp.
![]() $\mathfrak{su}(E)$
) the bundle of traceless (resp. traceless skew-Hermitian) endomorphisms of
$\mathfrak{su}(E)$
) the bundle of traceless (resp. traceless skew-Hermitian) endomorphisms of
![]() $E$
. Let
$E$
. Let
![]() $A$
be a unitary (with respect to
$A$
be a unitary (with respect to
![]() $H_0$
) connection on
$H_0$
) connection on
![]() $E$
that induces the trivial connection on
$E$
that induces the trivial connection on
![]() $\det E$
, and let
$\det E$
, and let
![]() $\phi \in \Omega^1(i\mathfrak{su}(E))$
. We will sometimes also refer to
$\phi \in \Omega^1(i\mathfrak{su}(E))$
. We will sometimes also refer to
![]() $\phi$
as a Higgs field. The Hitchin equations for the pair
$\phi$
as a Higgs field. The Hitchin equations for the pair
![]() $(A,\phi )$
are given by
$(A,\phi )$
are given by
If we split the Higgs field into type
![]() $\phi = \varphi + \varphi ^{\dagger }$
, with
$\phi = \varphi + \varphi ^{\dagger }$
, with
![]() $\varphi \in \Omega ^{1,0}(\mathfrak{sl}(E))$
, then (5) is equivalent to
$\varphi \in \Omega ^{1,0}(\mathfrak{sl}(E))$
, then (5) is equivalent to
Notice that
![]() $(\bar \partial _E,\varphi )$
then defines an
$(\bar \partial _E,\varphi )$
then defines an
![]() ${\rm SL}(2,\mathbb{C})$
Higgs bundle. The Hitchin moduli space, denoted by
${\rm SL}(2,\mathbb{C})$
Higgs bundle. The Hitchin moduli space, denoted by
![]() $\mathcal{M}_{{\rm Hit}}$
, is the moduli space of solutions to the Hitchin equations, which is given by
$\mathcal{M}_{{\rm Hit}}$
, is the moduli space of solutions to the Hitchin equations, which is given by
where
![]() $\mathcal{G}$
is the gauge group of unitary automorphisms of
$\mathcal{G}$
is the gauge group of unitary automorphisms of
![]() $E$
. Recall that a flat connection
$E$
. Recall that a flat connection
![]() $\mathcal{D}$
is called completely reducible if and only if it is a direct sum of irreducible flat connections. The NAH can be summarized as follows:
$\mathcal{D}$
is called completely reducible if and only if it is a direct sum of irreducible flat connections. The NAH can be summarized as follows:
Theorem 2.5.
A Higgs bundle
![]() $(\mathcal{E},\varphi )$
is polystable if and only if there exists a Hermitian metric
$(\mathcal{E},\varphi )$
is polystable if and only if there exists a Hermitian metric
![]() $H$
such that the corresponding Chern connection
$H$
such that the corresponding Chern connection
![]() $A$
and Higgs field
$A$
and Higgs field
![]() $\phi =\varphi +\varphi ^{\dagger }$
solve the Hitchin equations
(5)
. Moreover, the connection
$\phi =\varphi +\varphi ^{\dagger }$
solve the Hitchin equations
(5)
. Moreover, the connection
![]() $\mathcal{D}$
defined by
$\mathcal{D}$
defined by
![]() $\mathcal{D}=\nabla _A+\phi$
is a completely reducible flat connection, and it is irreducible if and only if
$\mathcal{D}=\nabla _A+\phi$
is a completely reducible flat connection, and it is irreducible if and only if
![]() $(\mathcal{E},\varphi )$
is stable.
$(\mathcal{E},\varphi )$
is stable.
Conversely, a flat connection
![]() $\mathcal{D}$
is completely reducible if and only if there exists a Hermitian metric
$\mathcal{D}$
is completely reducible if and only if there exists a Hermitian metric
![]() $H$
on
$H$
on
![]() $E$
such that when we express
$E$
such that when we express
![]() $\mathcal{D}=\nabla _A+\varphi +\varphi ^{\dagger }$
, we have
$\mathcal{D}=\nabla _A+\varphi +\varphi ^{\dagger }$
, we have
![]() $\bar{\partial }_{\mathcal{E}}\varphi=0$
. Moreover, the corresponding Higgs bundle
$\bar{\partial }_{\mathcal{E}}\varphi=0$
. Moreover, the corresponding Higgs bundle
![]() $(\mathcal{E},\varphi )$
is polystable, and it is stable if and only if
$(\mathcal{E},\varphi )$
is polystable, and it is stable if and only if
![]() $\mathcal{D}$
is irreducible.
$\mathcal{D}$
is irreducible.
The nonabelian Hodge correspondence gives the Kobayashi–Hitchin homeomorphism (1), which, when restricted to the stable locus, is a diffeomorphism onto irreducible solutions of (5).
Finally, we note that there is an action of
![]() $S^1$
on
$S^1$
on
![]() $\mathcal{M}_{{\rm Hit}}$
defined by
$\mathcal{M}_{{\rm Hit}}$
defined by
![]() $(A,\phi ) \to (A,e^{i\theta }\cdot \phi )$
, where
$(A,\phi ) \to (A,e^{i\theta }\cdot \phi )$
, where
![]() $e^{i\theta }\cdot \phi =e^{i\theta }\varphi +e^{-i\theta }\varphi ^\dagger$
. With respect to this and the
$e^{i\theta }\cdot \phi =e^{i\theta }\varphi +e^{-i\theta }\varphi ^\dagger$
. With respect to this and the
![]() $S^1\subset \mathbb{C}^\ast$
action on
$S^1\subset \mathbb{C}^\ast$
action on
![]() $\mathcal{M}_{{\rm Dol}}$
, the map
$\mathcal{M}_{{\rm Dol}}$
, the map
![]() $\Xi$
is
$\Xi$
is
![]() $S^1$
-equivariant.
$S^1$
-equivariant.
3. Filtered bundles and compactness
Filtered (or parabolic) bundles are described, for example, in [Reference SimpsonSim90]. They play a key role in the analytic compactification. This section provides a brief overview of filtered line bundles and demonstrates a compactness result.
3.1 Filtered line bundles
Let
![]() $Z$
be a finite collection of distinct points on a closed Riemann surface
$Z$
be a finite collection of distinct points on a closed Riemann surface
![]() $\Sigma$
, and let
$\Sigma$
, and let
![]() $\Sigma ^{\prime} = \Sigma \setminus Z$
. Viewing
$\Sigma ^{\prime} = \Sigma \setminus Z$
. Viewing
![]() $\Sigma$
as a projective algebraic curve, an algebraic line bundle
$\Sigma$
as a projective algebraic curve, an algebraic line bundle
![]() $L$
over the affine curve
$L$
over the affine curve
![]() $\Sigma ^{\prime}$
is a line bundle defined by regular transition functions on Zariski open sets over
$\Sigma ^{\prime}$
is a line bundle defined by regular transition functions on Zariski open sets over
![]() $\Sigma ^{\prime}$
. The sheaf of sections of
$\Sigma ^{\prime}$
. The sheaf of sections of
![]() $L$
can be extended in infinitely many different ways over
$L$
can be extended in infinitely many different ways over
![]() $Z$
to obtain (invertible) coherent analytic sheaves on
$Z$
to obtain (invertible) coherent analytic sheaves on
![]() $\Sigma$
. The sections of
$\Sigma$
. The sections of
![]() $L$
are then realised as meromorphic sections of any such extensions that are regular on
$L$
are then realised as meromorphic sections of any such extensions that are regular on
![]() $\Sigma ^{\prime}$
.
$\Sigma ^{\prime}$
.
A filtered line bundle
![]() $\mathcal{F}_{\ast }(L)$
is an algebraic line bundle
$\mathcal{F}_{\ast }(L)$
is an algebraic line bundle
![]() $L\to \Sigma ^{\prime}$
, along with a collection
$L\to \Sigma ^{\prime}$
, along with a collection
![]() $\{L_{\alpha }\}_{\alpha \in \mathbb R}$
of coherent extensions across the punctures
$\{L_{\alpha }\}_{\alpha \in \mathbb R}$
of coherent extensions across the punctures
![]() $ Z$
, such that
$ Z$
, such that
![]() $L_{\alpha } \subset L_{\beta }$
for
$L_{\alpha } \subset L_{\beta }$
for
![]() $\alpha \geq \beta$
for fixed, sufficiently small
$\alpha \geq \beta$
for fixed, sufficiently small
![]() $\epsilon$
,
$\epsilon$
,
![]() $L_{\alpha -\epsilon }=L_{\alpha }$
and
$L_{\alpha -\epsilon }=L_{\alpha }$
and
![]() $L_{\alpha } = L_{\alpha+1} \otimes \mathcal{O}_\Sigma (Z)$
. Let
$L_{\alpha } = L_{\alpha+1} \otimes \mathcal{O}_\Sigma (Z)$
. Let
![]() ${\rm Gr}_{\alpha }= L_{\alpha }/L_{\alpha +\epsilon }$
denote the quotient (torsion) sheaf. A value
${\rm Gr}_{\alpha }= L_{\alpha }/L_{\alpha +\epsilon }$
denote the quotient (torsion) sheaf. A value
![]() $\alpha$
where
$\alpha$
where
![]() ${\rm Gr}_{\alpha } \neq 0$
is called a jump. Since we are considering line bundles, for each
${\rm Gr}_{\alpha } \neq 0$
is called a jump. Since we are considering line bundles, for each
![]() $p$
in the support of
$p$
in the support of
![]() ${\rm Gr}_{\alpha _p}$
, there is exactly one jump
${\rm Gr}_{\alpha _p}$
, there is exactly one jump
![]() $\alpha _p$
in the interval
$\alpha _p$
in the interval
![]() $[0,1)$
. The collection of jumps
$[0,1)$
. The collection of jumps
![]() $\alpha _p$
,
$\alpha _p$
,
![]() $p\in Z$
, fully determines the filtered bundle structure. If we denote by
$p\in Z$
, fully determines the filtered bundle structure. If we denote by
![]() $\mathcal{L}:=L_{0}$
, the degree of a filtered line bundle is defined as
$\mathcal{L}:=L_{0}$
, the degree of a filtered line bundle is defined as
Alternatively, a weighted line bundle is a pair
![]() $(\mathcal{L},\chi )$
for which
$(\mathcal{L},\chi )$
for which
![]() $\mathcal{L}\to \Sigma$
is a holomorphic line bundle and
$\mathcal{L}\to \Sigma$
is a holomorphic line bundle and
![]() $\chi :Z\to \mathbb{R}$
is a weight function. The degree of a weighted bundle is defined as
$\chi :Z\to \mathbb{R}$
is a weight function. The degree of a weighted bundle is defined as
The notions of filtered and weighted line bundles are nearly equivalent: Namely, given a filtered line bundle
![]() $\mathcal{F}_{\ast }(L)$
, we define
$\mathcal{F}_{\ast }(L)$
, we define
![]() $\mathcal{L}:=L_{0}$
and
$\mathcal{L}:=L_{0}$
and
![]() $\chi _p=\alpha _p$
. Conversely, given a weighted line bundle
$\chi _p=\alpha _p$
. Conversely, given a weighted line bundle
![]() $(\mathcal{L},\chi )$
, we let
$(\mathcal{L},\chi )$
, we let
![]() $\alpha _p=\chi _p+n_p$
, where
$\alpha _p=\chi _p+n_p$
, where
![]() $n_p\in \mathbb{Z}$
is the unique integer and
$n_p\in \mathbb{Z}$
is the unique integer and
![]() $0\leq \chi _p+n_p\lt 1$
. A filtered bundle
$0\leq \chi _p+n_p\lt 1$
. A filtered bundle
![]() $\mathcal{F}_{\ast }(L)$
,
$\mathcal{F}_{\ast }(L)$
,
![]() $L:=\mathcal{L}\bigr |_{\Sigma ^{\prime}}$
, is then determined by setting
$L:=\mathcal{L}\bigr |_{\Sigma ^{\prime}}$
, is then determined by setting
![]() $L_{0} = \mathcal{L}(-\sum _{p\in Z} n_p p)$
with jumps
$L_{0} = \mathcal{L}(-\sum _{p\in Z} n_p p)$
with jumps
![]() $\alpha _p$
. Clearly,
$\alpha _p$
. Clearly,
![]() $\deg (\mathcal{F}(L))=\deg (\mathcal{L},\chi )$
. We shall use the notation
$\deg (\mathcal{F}(L))=\deg (\mathcal{L},\chi )$
. We shall use the notation
![]() $\mathcal{F}_{\ast }(\mathcal{L},\chi )$
for the filtered bundle associated to a weighted bundle
$\mathcal{F}_{\ast }(\mathcal{L},\chi )$
for the filtered bundle associated to a weighted bundle
![]() $(\mathcal{L},\chi )$
in this way.
$(\mathcal{L},\chi )$
in this way.
Different weighted bundles can give rise to the same filtered bundle. The following is a fact that will be frequently used in this article. If
![]() $D=\sum _{x\in Z}d_xx$
is a divisor supported on
$D=\sum _{x\in Z}d_xx$
is a divisor supported on
![]() $Z$
, let
$Z$
, let
 \begin{align*} \chi _D(x) & :=\begin {cases}d_x & x\in Z\;\\ 0\, & x\in \Sigma \setminus Z. \end {cases} \end{align*}
\begin{align*} \chi _D(x) & :=\begin {cases}d_x & x\in Z\;\\ 0\, & x\in \Sigma \setminus Z. \end {cases} \end{align*}
Then for any weighted bundle
![]() $(\mathcal{L},\chi )$
, we have
$(\mathcal{L},\chi )$
, we have
![]() $\mathcal{F}_\ast (\mathcal{L}(D),\chi -\chi _{D})=\mathcal{F}_\ast (\mathcal{L},\chi )$
.
$\mathcal{F}_\ast (\mathcal{L}(D),\chi -\chi _{D})=\mathcal{F}_\ast (\mathcal{L},\chi )$
.
Let
![]() $(\mathcal{L}_1,\chi _1)$
and
$(\mathcal{L}_1,\chi _1)$
and
![]() $(\mathcal{L}_2,\chi _2)$
be two weighted lines bundles. We define the tensor product
$(\mathcal{L}_2,\chi _2)$
be two weighted lines bundles. We define the tensor product
Then the degree is additive on tensor products. For filtered bundles, we define
The degree is again additive for the tensor product of filtered bundles. This agrees with the usual definition of tensor product for parabolic bundles.
3.2 Harmonic metrics for weighted line bundles
Proposition 3.1.
Let
![]() $(\mathcal{L},\chi )$
be a degree-0 weighted bundle. Then there exists a Hermitian metric
$(\mathcal{L},\chi )$
be a degree-0 weighted bundle. Then there exists a Hermitian metric
![]() $h$
on
$h$
on
![]() $\mathcal{L}_{\Sigma ^{\prime}}$
, which is unique up to a multiplication by a nonzero constant, such that:
$\mathcal{L}_{\Sigma ^{\prime}}$
, which is unique up to a multiplication by a nonzero constant, such that:
-
(i) the Chern connection
 $A_h$
of
$A_h$
of
 $(\mathcal{L},h)$
is flat:
$(\mathcal{L},h)$
is flat:
 $F_{A_h}=0$
;
$F_{A_h}=0$
; -
(ii) for
 $p\in Z$
and
$p\in Z$
and
 $(U_p,z)$
, a holomorphic coordinate centered at
$(U_p,z)$
, a holomorphic coordinate centered at
 $p$
,
$p$
,
 $|z|^{-2\chi _p}h$
extends to a
$|z|^{-2\chi _p}h$
extends to a
 $\mathcal{C}^{\infty }$
Hermitian metric on
$\mathcal{C}^{\infty }$
Hermitian metric on
 $\mathcal{L}|_{U_p}$
.
$\mathcal{L}|_{U_p}$
.
Proof.
We first choose a background Hermitian metric
![]() $h_0$
such that
$h_0$
such that
![]() $|z|^{-2\chi _p}h_0$
defines a
$|z|^{-2\chi _p}h_0$
defines a
![]() $\mathcal{C}^{\infty }$
Hermitian metric defined on
$\mathcal{C}^{\infty }$
Hermitian metric defined on
![]() $U_p$
. Let
$U_p$
. Let
![]() $A_{h_0}$
be the Chern connection, and let
$A_{h_0}$
be the Chern connection, and let
![]() $F_{A_0}$
be the curvature. Note that
$F_{A_0}$
be the curvature. Note that
![]() $F_{A_0}$
is smooth on
$F_{A_0}$
is smooth on
![]() $\Sigma$
. By the Poincaré–Lelong formula, we have
$\Sigma$
. By the Poincaré–Lelong formula, we have
![]() ${\sqrt{-1} \over 2\pi }\int _{\Sigma }F_{A_0}=\deg (\mathcal{L},\chi )=0$
. Therefore, there exists a
${\sqrt{-1} \over 2\pi }\int _{\Sigma }F_{A_0}=\deg (\mathcal{L},\chi )=0$
. Therefore, there exists a
![]() $\mathcal{C}^{\infty }$
function
$\mathcal{C}^{\infty }$
function
![]() $\rho$
such that
$\rho$
such that
![]() $\Delta \rho +{\sqrt{-1} \over 2\pi }\Lambda F_{A_0}=0$
. We define
$\Delta \rho +{\sqrt{-1} \over 2\pi }\Lambda F_{A_0}=0$
. We define
![]() $h=h_0e^{\rho }$
. For the corresponding Chern connection
$h=h_0e^{\rho }$
. For the corresponding Chern connection
![]() $A_h$
, we have
$A_h$
, we have
![]() $F_{A_h}=0$
, which implies (i). Then (ii) follows from the property for
$F_{A_h}=0$
, which implies (i). Then (ii) follows from the property for
![]() $h_0$
since
$h_0$
since
![]() $\rho$
is a smooth function on
$\rho$
is a smooth function on
![]() $\Sigma$
. As
$\Sigma$
. As
![]() $\rho$
is well-defined up to a constant,
$\rho$
is well-defined up to a constant,
![]() $h$
is also well-defined up to a constant, which implies the uniqueness of
$h$
is also well-defined up to a constant, which implies the uniqueness of
![]() $h$
up to a constant.
$h$
up to a constant.
The metric obtained above is called the harmonic metric. For a weighted bundle
![]() $(\mathcal{L},\chi )$
, the holomorphic bundle
$(\mathcal{L},\chi )$
, the holomorphic bundle
![]() $\mathcal{L}$
and the harmonic metric
$\mathcal{L}$
and the harmonic metric
![]() $h$
define a filtration as follows: Given
$h$
define a filtration as follows: Given
![]() $\alpha$
, define the sheaf
$\alpha$
, define the sheaf
and any open set
![]() $U\subset \Sigma$
. Here,
$U\subset \Sigma$
. Here,
![]() $r$
denotes the distance to
$r$
denotes the distance to
![]() $Z$
in any smooth, conformal metric on
$Z$
in any smooth, conformal metric on
![]() $\Sigma$
. It is straightforward to check that this defines a filtered bundle that matches
$\Sigma$
. It is straightforward to check that this defines a filtered bundle that matches
![]() $\mathcal{F}_\ast (\mathcal{L},\chi )$
under the correspondence given in the previous section.
$\mathcal{F}_\ast (\mathcal{L},\chi )$
under the correspondence given in the previous section.
Even though the harmonic metric is well-defined only up to a constant, the Chern connection
![]() $A=(\mathcal{L},h)$
is independent of this choice. The
$A=(\mathcal{L},h)$
is independent of this choice. The
![]() $(1,0)$
part of
$(1,0)$
part of
![]() $A$
, denoted
$A$
, denoted
![]() $\nabla _h$
, then defines logarithmic the connections
$\nabla _h$
, then defines logarithmic the connections
![]() $\nabla _h:L_{\alpha }\to L_{\alpha }\otimes K(Z).$
$\nabla _h:L_{\alpha }\to L_{\alpha }\otimes K(Z).$
3.3 Convergence of weighted line bundles
In this subsection, we consider the convergence of weighted line bundles. The main result we prove here is a consequence of [Reference Mochizuki and SzabóMS23, Theorem 1.8]. For the reader’s convenience, we present a short proof in our situation.
Let
![]() $(\Sigma _0,g_0)$
be a metrised Riemann surface (that is, a Riemann surface
$(\Sigma _0,g_0)$
be a metrised Riemann surface (that is, a Riemann surface
![]() $\Sigma _0$
with conformal metric
$\Sigma _0$
with conformal metric
![]() $g_0$
). We view
$g_0$
). We view
![]() $\Sigma _0$
as given by an underlying surface
$\Sigma _0$
as given by an underlying surface
![]() $C$
with almost complex structure
$C$
with almost complex structure
![]() $J_0$
. Consider a neighbourhood
$J_0$
. Consider a neighbourhood
![]() $U_1$
of
$U_1$
of
![]() $J_0$
in the moduli space of holomorphic structures and a neighbourhood
$J_0$
in the moduli space of holomorphic structures and a neighbourhood
![]() $U_2$
of
$U_2$
of
![]() $g_0$
in the space of smooth metrics. We denote the product of these neighbourhoods by
$g_0$
in the space of smooth metrics. We denote the product of these neighbourhoods by
![]() $U=U_1\times U_2$
. We can define the fibre bundle
$U=U_1\times U_2$
. We can define the fibre bundle
![]() ${\rm Pic}_U \to U$
, where each fibre is the Picard group defined by the holomorphic structure. Let
${\rm Pic}_U \to U$
, where each fibre is the Picard group defined by the holomorphic structure. Let
![]() $(\Sigma _t=(C,J_t),g_t)$
be a family of metrised Riemann surfaces that converge smoothly to
$(\Sigma _t=(C,J_t),g_t)$
be a family of metrised Riemann surfaces that converge smoothly to
![]() $(\Sigma _0,g_0)$
as
$(\Sigma _0,g_0)$
as
![]() $t\to 0$
. Let
$t\to 0$
. Let
![]() $Z_t\subset \Sigma _t$
be a collection of a finite number of points that converge to
$Z_t\subset \Sigma _t$
be a collection of a finite number of points that converge to
![]() $Z_0$
in suitable symmetric products of
$Z_0$
in suitable symmetric products of
![]() $C$
. For each
$C$
. For each
![]() $p\in Z_0$
, we can write
$p\in Z_0$
, we can write
![]() $Z_t=\cup _{p\in Z_0}Z_{t,p}$
such that all points in
$Z_t=\cup _{p\in Z_0}Z_{t,p}$
such that all points in
![]() $Z_{t,p}$
converge to
$Z_{t,p}$
converge to
![]() $p$
. We define the convergence of weighted line bundles as follows:
$p$
. We define the convergence of weighted line bundles as follows:
Definition 3.2.
A family of weighted line bundles
![]() $(\mathcal{L}_t,\chi _t)$
over
$(\mathcal{L}_t,\chi _t)$
over
![]() $\Sigma _t\setminus Z_t$
, with weights
$\Sigma _t\setminus Z_t$
, with weights
![]() $\chi _t:Z_t\to \mathbb{R}$
, converges to
$\chi _t:Z_t\to \mathbb{R}$
, converges to
![]() $(\mathcal{L}_0,\chi _0)$
if
$(\mathcal{L}_0,\chi _0)$
if
-
(i)
 $\mathcal{L}_t$
converges to
$\mathcal{L}_t$
converges to
 $\mathcal{L}_0$
in
$\mathcal{L}_0$
in
 ${\rm Pic}_U$
and if
${\rm Pic}_U$
and if -
(ii) for all
 $p\in Z_0$
and
$p\in Z_0$
and
 $t$
sufficiently small,
$t$
sufficiently small,
 $\sum _{q\in Z_{t,p}}\chi _t(q)=\chi _0(p)$
.
$\sum _{q\in Z_{t,p}}\chi _t(q)=\chi _0(p)$
.
A sequence of filtered bundles
![]() $\mathcal{F}_{\ast }(\mathcal{L}_t)$
converges to
$\mathcal{F}_{\ast }(\mathcal{L}_t)$
converges to
![]() $\mathcal{F}_{\ast }(\mathcal{L}_0)$
if the corresponding weighted bundles converge. The following theorem provides insight into the compactness of a sequence of weighted line bundles:
$\mathcal{F}_{\ast }(\mathcal{L}_0)$
if the corresponding weighted bundles converge. The following theorem provides insight into the compactness of a sequence of weighted line bundles:
Theorem 3.3.
Consider a family of weighted line bundles
![]() $(\mathcal{L}_t,\chi _t)$
defined over
$(\mathcal{L}_t,\chi _t)$
defined over
![]() $(\Sigma _t\setminus Z_t)$
and with
$(\Sigma _t\setminus Z_t)$
and with
![]() $\deg (\mathcal{L}_t,\chi _t)=0$
. Let
$\deg (\mathcal{L}_t,\chi _t)=0$
. Let
![]() $h_t$
be the corresponding harmonic metrics from Proposition 3.1
. If
$h_t$
be the corresponding harmonic metrics from Proposition 3.1
. If
![]() $Z_t$
converges to
$Z_t$
converges to
![]() $Z_0$
, we write
$Z_0$
, we write
![]() $Z_t=\cup _{p\in Z_0}Z_{t,p}$
. Then there exists a weighted line bundle
$Z_t=\cup _{p\in Z_0}Z_{t,p}$
. Then there exists a weighted line bundle
![]() $(\mathcal{L}_0,\chi _0)$
over
$(\mathcal{L}_0,\chi _0)$
over
![]() $Z_0$
with a harmonic metric
$Z_0$
with a harmonic metric
![]() $h_0$
such that
$h_0$
such that
-
(i) After rescaling by
 $c_t\gt 0$
,
$c_t\gt 0$
,
 $c_th_t$
converges to
$c_th_t$
converges to
 $h_0$
over
$h_0$
over
 $\Sigma _0\setminus Z_0$
in the
$\Sigma _0\setminus Z_0$
in the
 $\mathcal{C}^{\infty }_{{\rm loc}}$
sense.
$\mathcal{C}^{\infty }_{{\rm loc}}$
sense.
-
(ii) If
 $A_{h_t}$
is the Chern connection of
$A_{h_t}$
is the Chern connection of
 $(\mathcal{L}_t,h_t)$
, then on
$(\mathcal{L}_t,h_t)$
, then on
 $\Sigma _0\setminus Z_0$
,
$\Sigma _0\setminus Z_0$
,
 $\lim _{t\to 0}\nabla _t=\nabla _0$
in
$\lim _{t\to 0}\nabla _t=\nabla _0$
in
 $\mathcal{C}^{\infty }_{{\rm loc}}$
.
$\mathcal{C}^{\infty }_{{\rm loc}}$
.
Proof.
By the assumptions on weights,
![]() $\deg (\mathcal{L}_t)$
is a fixed,
$\deg (\mathcal{L}_t)$
is a fixed,
![]() $t$
-independent constant. Let
$t$
-independent constant. Let
![]() $\gamma _t=(J_t,g_t)$
be a path in
$\gamma _t=(J_t,g_t)$
be a path in
![]() $U$
. Then
$U$
. Then
![]() ${\rm Pic}_U|_{\gamma _t}$
is compact, and there exists an
${\rm Pic}_U|_{\gamma _t}$
is compact, and there exists an
![]() $\mathcal{L}_0\in {\rm Pic}(\Sigma _0)$
such that
$\mathcal{L}_0\in {\rm Pic}(\Sigma _0)$
such that
![]() $\mathcal{L}_t$
converges to
$\mathcal{L}_t$
converges to
![]() $\mathcal{L}_0$
. For
$\mathcal{L}_0$
. For
![]() $p\in Z_0$
, define
$p\in Z_0$
, define
![]() $\chi _0(p)=\sum _{q\in Z_{t,p}}\chi _t(q)$
, after which you will obtain a weighted line bundle
$\chi _0(p)=\sum _{q\in Z_{t,p}}\chi _t(q)$
, after which you will obtain a weighted line bundle
![]() $(\mathcal{L}_0,\chi _0)$
. Choose a family of approximate harmonic metrics
$(\mathcal{L}_0,\chi _0)$
. Choose a family of approximate harmonic metrics
![]() $h_t^{{\rm app}}$
such that
$h_t^{{\rm app}}$
such that
![]() $|z|^{-2\chi _p}h_t^{{\rm app}}$
extends to a smooth metric in a neighbourhood of
$|z|^{-2\chi _p}h_t^{{\rm app}}$
extends to a smooth metric in a neighbourhood of
![]() $p$
, and
$p$
, and
![]() $h_t^{{\rm app}}$
converges to
$h_t^{{\rm app}}$
converges to
![]() $h_0^{{\rm app}}$
in
$h_0^{{\rm app}}$
in
![]() $\mathcal{C}^{\infty }_{{\rm loc}}(\Sigma _0\setminus Z_0)$
. Moreover, write
$\mathcal{C}^{\infty }_{{\rm loc}}(\Sigma _0\setminus Z_0)$
. Moreover, write
![]() $h_t=h_t^{{\rm app}}e^{s_t}$
. After a suitable rescaling of
$h_t=h_t^{{\rm app}}e^{s_t}$
. After a suitable rescaling of
![]() $h_t$
, we can assume
$h_t$
, we can assume
![]() $\|s_t\|_{L^2}=1$
. Let
$\|s_t\|_{L^2}=1$
. Let
![]() $\rho _t:=\Delta _th_t^{{\rm app}}$
be the curvature defined by the metric
$\rho _t:=\Delta _th_t^{{\rm app}}$
be the curvature defined by the metric
![]() $h^{{\rm app}}_t$
. Then
$h^{{\rm app}}_t$
. Then
![]() $s_t$
satisfies the equation
$s_t$
satisfies the equation
![]() $\Delta _ts_t=\rho _t$
over
$\Delta _ts_t=\rho _t$
over
![]() $\Sigma$
. As
$\Sigma$
. As
![]() $\rho _t$
converges to
$\rho _t$
converges to
![]() $\rho _0\in \mathcal{C}^{\infty }_{{\rm loc}}(\Sigma \setminus Z_0)$
and as
$\rho _0\in \mathcal{C}^{\infty }_{{\rm loc}}(\Sigma \setminus Z_0)$
and as
![]() $g_t$
is a family with bounded geometry, we obtain the estimate
$g_t$
is a family with bounded geometry, we obtain the estimate
where
![]() $C_{k,\alpha }$
is a
$C_{k,\alpha }$
is a
![]() $t$
-independent constant. Therefore, passing to a subsequence,
$t$
-independent constant. Therefore, passing to a subsequence,
![]() $s_t$
converges to
$s_t$
converges to
![]() $s_0$
in
$s_0$
in
![]() $\mathcal{C}^{\infty }(\Sigma )$
, which implies (i). The assertion (ii) follows from (i).
$\mathcal{C}^{\infty }(\Sigma )$
, which implies (i). The assertion (ii) follows from (i).
4. The algebraic and analytic compactifications
4.1 The algebraic compactification of the Dolbeault moduli space
In this subsection, we present the algebraic method for compactifying the Dolbeault moduli space. This technique is based on the
![]() $\mathbb{C}^{\ast }$
action on
$\mathbb{C}^{\ast }$
action on
![]() $\mathcal{M}_{{\rm Dol}}$
and was introduced in [Reference SimpsonSim97, Reference SchmittSch98, Reference HauselHau98, Reference de CataldodC21, Reference Katzarkov, Noll, Pandit and SimpsonKNPS15]. The gauge theoretic approach can be found in [Reference FanFan22a].
$\mathcal{M}_{{\rm Dol}}$
and was introduced in [Reference SimpsonSim97, Reference SchmittSch98, Reference HauselHau98, Reference de CataldodC21, Reference Katzarkov, Noll, Pandit and SimpsonKNPS15]. The gauge theoretic approach can be found in [Reference FanFan22a].
Theorem 4.1.
Let
![]() $V$
be a complex algebraic variety with
$V$
be a complex algebraic variety with
![]() $\mathbb{C}^{\ast }$
action. Suppose that
$\mathbb{C}^{\ast }$
action. Suppose that
-
(i) the fixed point set of the
 $\mathbb{C}^{\ast }$
action is proper and that
$\mathbb{C}^{\ast }$
action is proper and that
-
(ii) for every
 $t\in \mathbb{C}^{\ast },\;v\in V$
, the limit
$t\in \mathbb{C}^{\ast },\;v\in V$
, the limit
 $\displaystyle \lim _{t\to 0}t\cdot v$
exists.
$\displaystyle \lim _{t\to 0}t\cdot v$
exists.
Then the space
![]() $\displaystyle U:=\{v\in V\mid \lim _{t\to \infty }t\cdot v\;{\rm does\;not\;exist}\}$
is open in
$\displaystyle U:=\{v\in V\mid \lim _{t\to \infty }t\cdot v\;{\rm does\;not\;exist}\}$
is open in
![]() $V$
, and the quotient
$V$
, and the quotient
![]() $U/\mathbb{C}^{\ast }$
is separated and proper.
$U/\mathbb{C}^{\ast }$
is separated and proper.
We apply this to the Dolbeault moduli space. The first step is to note that the possible isotropy subgroups are limited.
Lemma 4.2.
Let
![]() $\xi =[(\mathcal{E},\varphi )]$
be an
$\xi =[(\mathcal{E},\varphi )]$
be an
![]() ${\rm SL}(2,\mathbb{C})$
Higgs bundle equivalence class with
${\rm SL}(2,\mathbb{C})$
Higgs bundle equivalence class with
![]() $\mathcal{H}(\xi )\neq 0$
. Then the stabiliser
$\mathcal{H}(\xi )\neq 0$
. Then the stabiliser
![]() $\Gamma _{\xi }$
of
$\Gamma _{\xi }$
of
![]() $\xi$
for the
$\xi$
for the
![]() $\mathbb{C}^{\ast }$
action is either trivial or
$\mathbb{C}^{\ast }$
action is either trivial or
![]() $\mathbb{Z}/2$
. The latter case holds if and only if
$\mathbb{Z}/2$
. The latter case holds if and only if
![]() $(\mathcal{E},\varphi )$
and
$(\mathcal{E},\varphi )$
and
![]() $(\mathcal{E},-\varphi )$
are complex gauge equivalent.
$(\mathcal{E},-\varphi )$
are complex gauge equivalent.
Proof.
For
![]() $t\in \Gamma _\xi$
,
$t\in \Gamma _\xi$
,
![]() $\mathcal{H}(\xi )=\mathcal{H}(t\cdot \xi )=t^2\mathcal{H}(\xi )$
. Hence,
$\mathcal{H}(\xi )=\mathcal{H}(t\cdot \xi )=t^2\mathcal{H}(\xi )$
. Hence,
![]() $t^2=1$
if
$t^2=1$
if
![]() $\mathcal{H}(\xi )\neq 0$
.
$\mathcal{H}(\xi )\neq 0$
.
By this lemma, the space
![]() $(\mathcal{M}_{{\rm Dol}}\setminus \mathcal{H}^{-1}(0))/\mathbb{C}^{\ast }$
has an orbifold structure. In passing, we note that the fixed points of the
$(\mathcal{M}_{{\rm Dol}}\setminus \mathcal{H}^{-1}(0))/\mathbb{C}^{\ast }$
has an orbifold structure. In passing, we note that the fixed points of the
![]() $\mathbb{Z}/2$
action correspond to real representations under the nonabelian Hodge correspondence [Reference HitchinHit87a, Sec. 10].
$\mathbb{Z}/2$
action correspond to real representations under the nonabelian Hodge correspondence [Reference HitchinHit87a, Sec. 10].
By the properness of the Hitchin map
![]() $\mathcal{H}$
(see Theorem 2.1), it follows that
$\mathcal{H}$
(see Theorem 2.1), it follows that
![]() $\displaystyle \lim _{t\to \infty }t\cdot \xi$
exists if and only if
$\displaystyle \lim _{t\to \infty }t\cdot \xi$
exists if and only if
![]() $\mathcal{H}(\xi )=0$
. Now define
$\mathcal{H}(\xi )=0$
. Now define
The analytic topology on the disjoint union is generated by open sets
![]() $U\times W_1$
and
$U\times W_1$
and
where
![]() $U,V\subset \mathcal{M}_{{\rm Dol}}$
,
$U,V\subset \mathcal{M}_{{\rm Dol}}$
,
![]() $W_1,W_2\subset \mathbb{C}$
are open, and
$W_1,W_2\subset \mathbb{C}$
are open, and
![]() $0\not \in W_1$
,
$0\not \in W_1$
,
![]() $0\in W_2$
. The topology on
$0\in W_2$
. The topology on
![]() $\overline{\mathcal{M}}_{{\rm Dol}}$
is then the quotient topology, and it is straightforward to see that with this topology, it is compact.
$\overline{\mathcal{M}}_{{\rm Dol}}$
is then the quotient topology, and it is straightforward to see that with this topology, it is compact.
Since
![]() $(\mathcal{M}_{{\rm Dol}} \times \mathbb{C}^{\ast })/\mathbb{C}^{\ast }=\mathcal{M}_{{\rm Dol}}$
, there is the natural inclusion
$(\mathcal{M}_{{\rm Dol}} \times \mathbb{C}^{\ast })/\mathbb{C}^{\ast }=\mathcal{M}_{{\rm Dol}}$
, there is the natural inclusion
where brackets denote the equivalence class under the
![]() $\mathbb{C}^{\ast }$
action. The boundary of
$\mathbb{C}^{\ast }$
action. The boundary of
![]() $\overline{\mathcal{M}}_{{\rm Dol}}$
is
$\overline{\mathcal{M}}_{{\rm Dol}}$
is
There is also the boundary map
which is invariant under the
![]() $\mathbb{C}^{\ast }$
action; that is,
$\mathbb{C}^{\ast }$
action; that is,
![]() $\iota _{\partial }(\lambda \xi ) = \iota _{\partial }(\xi )$
for
$\iota _{\partial }(\lambda \xi ) = \iota _{\partial }(\xi )$
for
![]() $\lambda \in \mathbb{C}^{\ast }$
.
$\lambda \in \mathbb{C}^{\ast }$
.
The
![]() $\mathbb{C}^{\ast }$
action on
$\mathbb{C}^{\ast }$
action on
![]() $\mathcal{M}_{{\rm Dol}}$
covers the square of the action on
$\mathcal{M}_{{\rm Dol}}$
covers the square of the action on
![]() $\mathcal{B}$
. Hence, it is natural to compactify
$\mathcal{B}$
. Hence, it is natural to compactify
![]() $\mathcal{B}$
by projectivising:
$\mathcal{B}$
by projectivising:
The inclusion is given, as usual, by
where
![]() $q\times \{1\}\in H^0(K^2)\oplus \mathbb{C}$
. We also define
$q\times \{1\}\in H^0(K^2)\oplus \mathbb{C}$
. We also define
![]() $\partial \overline{\mathcal{B}}=\overline{\mathcal{B}}\setminus \iota _0(\mathcal{B})\simeq \mathbb{P}(H^0(K^2))$
, with boundary projection map
$\partial \overline{\mathcal{B}}=\overline{\mathcal{B}}\setminus \iota _0(\mathcal{B})\simeq \mathbb{P}(H^0(K^2))$
, with boundary projection map
The Hitchin map
![]() $\mathcal{H}:\mathcal{M}_{{\rm Dol}}\to \mathcal{B}$
extends to
$\mathcal{H}:\mathcal{M}_{{\rm Dol}}\to \mathcal{B}$
extends to
![]() $\overline{\mathcal{H}}:\overline{\mathcal{M}}_{{\rm Dol}}\to \overline{\mathcal{B}}$
, where
$\overline{\mathcal{H}}:\overline{\mathcal{M}}_{{\rm Dol}}\to \overline{\mathcal{B}}$
, where
![]() $\overline{\mathcal{H}}|_{\mathcal{M}_{{\rm Dol}}}:=\iota _0\circ \mathcal{H}$
, and for every
$\overline{\mathcal{H}}|_{\mathcal{M}_{{\rm Dol}}}:=\iota _0\circ \mathcal{H}$
, and for every
![]() $[(\mathcal{E},\varphi )]/\mathbb{C}^{\ast }\in \partial \overline{\mathcal{M}}_{{\rm Dol}}$
,
$[(\mathcal{E},\varphi )]/\mathbb{C}^{\ast }\in \partial \overline{\mathcal{M}}_{{\rm Dol}}$
,
This is well-defined, since
![]() $\det (\varphi ) \neq 0$
if
$\det (\varphi ) \neq 0$
if
![]() $[(\mathcal{E},\varphi )]/\mathbb{C}^{\ast }\in \partial \overline{\mathcal{M}}_{{\rm Dol}}$
. Moreover,
$[(\mathcal{E},\varphi )]/\mathbb{C}^{\ast }\in \partial \overline{\mathcal{M}}_{{\rm Dol}}$
. Moreover,

commutes.
There is a good algebraic structure on this compactification.
Theorem 4.3.
The compactified space
![]() $\overline{\mathcal{M}}_{{\rm Dol}}$
is a normal projective variety, and
$\overline{\mathcal{M}}_{{\rm Dol}}$
is a normal projective variety, and
![]() $\partial \overline{\mathcal{M}}_{{\rm Dol}}$
is a Cartier divisor of
$\partial \overline{\mathcal{M}}_{{\rm Dol}}$
is a Cartier divisor of
![]() $\overline{\mathcal{M}}_{{\rm Dol}}$
.
$\overline{\mathcal{M}}_{{\rm Dol}}$
.
The following characterisation of sequential convergence is useful: As
![]() $H^0(K^2)$
is a finite dimensional space, the
$H^0(K^2)$
is a finite dimensional space, the
![]() $L^2$
norm on
$L^2$
norm on
![]() $q\in H^0(K_{\Sigma }^2)$
can be chosen arbitrarily, and we fix one such choice.
$q\in H^0(K_{\Sigma }^2)$
can be chosen arbitrarily, and we fix one such choice.
Proposition 4.4.
Let
![]() $[(\mathcal{E}_i,\varphi _i)]\in \mathcal{M}_{{\rm Dol}}$
be a sequence of Higgs bundles, and write
$[(\mathcal{E}_i,\varphi _i)]\in \mathcal{M}_{{\rm Dol}}$
be a sequence of Higgs bundles, and write
![]() $q_i=\det (\varphi _i)$
and
$q_i=\det (\varphi _i)$
and
![]() $r_i=\|q_i\|_{L^2}^{\frac 12}$
. Suppose
$r_i=\|q_i\|_{L^2}^{\frac 12}$
. Suppose
![]() $\limsup r_i\to \infty$
. Then up to the subsequence:
$\limsup r_i\to \infty$
. Then up to the subsequence:
-
(i) there exists a Higgs bundle
 $[(\widehat{\mathcal{E}}_{\infty },\hat{\varphi }_{\infty })]$
with
$[(\widehat{\mathcal{E}}_{\infty },\hat{\varphi }_{\infty })]$
with
 $\tilde{q}_{\infty }=\det (\tilde{\varphi }_{\infty })$
and
$\tilde{q}_{\infty }=\det (\tilde{\varphi }_{\infty })$
and
 $\|\hat{q}_{\infty }\|_{L^2}=1$
such that
$\|\hat{q}_{\infty }\|_{L^2}=1$
such that
 $\lim _{i\to \infty }[(\mathcal{E}_i,r_i^{-1}\varphi _i)]=[(\widehat{\mathcal{E}}_{\infty },\hat{\varphi }_{\infty })]$
in
$\lim _{i\to \infty }[(\mathcal{E}_i,r_i^{-1}\varphi _i)]=[(\widehat{\mathcal{E}}_{\infty },\hat{\varphi }_{\infty })]$
in
 $\mathcal{M}_{{\rm Dol}}$
and
$\mathcal{M}_{{\rm Dol}}$
and
 $\lim _{i\to \infty }r_i^{-1}q_i=\hat{q}_{\infty }$
in
$\lim _{i\to \infty }r_i^{-1}q_i=\hat{q}_{\infty }$
in
 $H^0(K^2)$
;
$H^0(K^2)$
; -
(ii)
 \begin{align*} \lim _{i \to \infty } \iota [(\mathcal{E}_i,\varphi _i)] & =\iota _{\partial }[(\widehat{\mathcal{E}}_{\infty },\hat{\varphi }_{\infty })]\,\ \mbox{on}\ \overline{\mathcal{M}}_{{\rm Dol}}\, and \\ \lim _{i\to \infty }\iota _0(q_i) & =\iota _{0,\partial }(\hat{q}_{\infty })\,\ \mbox{on}\ \overline{\mathcal{B}}. \end{align*}
\begin{align*} \lim _{i \to \infty } \iota [(\mathcal{E}_i,\varphi _i)] & =\iota _{\partial }[(\widehat{\mathcal{E}}_{\infty },\hat{\varphi }_{\infty })]\,\ \mbox{on}\ \overline{\mathcal{M}}_{{\rm Dol}}\, and \\ \lim _{i\to \infty }\iota _0(q_i) & =\iota _{0,\partial }(\hat{q}_{\infty })\,\ \mbox{on}\ \overline{\mathcal{B}}. \end{align*}
Proof.
The first point follows since the Hitchin map
![]() $\mathcal{H}$
is proper and since
$\mathcal{H}$
is proper and since
![]() $\mathcal{H}(r_i^{-1}\varphi _i)$
is bounded. The second point follows directly from the definition.
$\mathcal{H}(r_i^{-1}\varphi _i)$
is bounded. The second point follows directly from the definition.
4.2 The analytic compactification of the Hitchin moduli space
We next describe the compactification of the Hitchin moduli space, as developed in [Reference Mazzeo, Swoboda, Weiß and WittMSWW14, Reference MochizukiMoc16, Reference TaubesTau13a].
4.2.1 Decoupled Hitchin equations
We begin by defining the decoupled Hitchin equations. Recalling the notation from Section 2.4, let
![]() $E$
be a trivial, smooth, rank 2 vector bundle over a Riemann surface
$E$
be a trivial, smooth, rank 2 vector bundle over a Riemann surface
![]() $\Sigma$
, and let
$\Sigma$
, and let
![]() $H_0$
be a background Hermitian metric on
$H_0$
be a background Hermitian metric on
![]() $E$
. Let
$E$
. Let
![]() $Z$
be a finite set of distinct points in
$Z$
be a finite set of distinct points in
![]() $\Sigma$
. For a smooth unitary connection
$\Sigma$
. For a smooth unitary connection
![]() $A$
on
$A$
on
![]() $E|_{\Sigma \setminus Z}$
and a smooth
$E|_{\Sigma \setminus Z}$
and a smooth
![]() $\phi =\varphi +\varphi ^{\dagger }\in \Omega^1(i\mathfrak{su}(E))|_{\Sigma \setminus Z}$
, the decoupled Hitchin equations on
$\phi =\varphi +\varphi ^{\dagger }\in \Omega^1(i\mathfrak{su}(E))|_{\Sigma \setminus Z}$
, the decoupled Hitchin equations on
![]() $\Sigma \setminus Z$
are:
$\Sigma \setminus Z$
are:
Solutions to (9) alone may be quite singular near
![]() $Z$
, so we make the following restriction:
$Z$
, so we make the following restriction:
Definition 4.5.
A solution
![]() $(A,\phi )$
to
(9)
is called admissible if
$(A,\phi )$
to
(9)
is called admissible if
![]() $\phi \neq 0$
and if
$\phi \neq 0$
and if
![]() $|\phi |$
extends to a continuous function on
$|\phi |$
extends to a continuous function on
![]() $\Sigma$
with
$\Sigma$
with
![]() $|\phi |^{-1}(0)=Z$
.
$|\phi |^{-1}(0)=Z$
.
By a limiting configuration, we always mean an admissible solution to the decoupled Hitchin equations. Clearly,
![]() $Z$
is determined by
$Z$
is determined by
![]() $(A,\phi )$
. Admissibility guarantees that
$(A,\phi )$
. Admissibility guarantees that
![]() $\det (\varphi )$
extends to a holomorphic quadratic differential
$\det (\varphi )$
extends to a holomorphic quadratic differential
![]() $q=\det (\varphi )$
on
$q=\det (\varphi )$
on
![]() $\Sigma$
, with
$\Sigma$
, with
![]() $Z=q^{-1}(0)$
being the zero locus. Hence, the spectral curve
$Z=q^{-1}(0)$
being the zero locus. Hence, the spectral curve
![]() $S_q$
is well-defined. We emphasize that
$S_q$
is well-defined. We emphasize that
![]() $Z$
may vary for different admissible solutions, but one always has
$Z$
may vary for different admissible solutions, but one always has
![]() $\# Z\leq 4g-4$
.
$\# Z\leq 4g-4$
.
The equivalence relation on limiting configurations is that
![]() $(A_1,\phi _1)\sim (A_2,\phi _2)$
if
$(A_1,\phi _1)\sim (A_2,\phi _2)$
if
![]() $Z_1=Z_2$
and if
$Z_1=Z_2$
and if
![]() $(A_1,\phi _1)g=(A_2,\phi _2)$
for a smooth unitary gauge transformation
$(A_1,\phi _1)g=(A_2,\phi _2)$
for a smooth unitary gauge transformation
![]() $g$
on
$g$
on
![]() $\Sigma \setminus Z_1$
. The moduli space of decoupled Hitchin equations is then
$\Sigma \setminus Z_1$
. The moduli space of decoupled Hitchin equations is then
We denote by
![]() $\mathcal{M}_{{\rm Hit},q}^{{\rm Lim}}$
the elements in
$\mathcal{M}_{{\rm Hit},q}^{{\rm Lim}}$
the elements in
![]() $\mathcal{M}_{{\rm Hit}}^{{\rm Lim}}$
, with the determinant of the Higgs field equal to a quadratic differential
$\mathcal{M}_{{\rm Hit}}^{{\rm Lim}}$
, with the determinant of the Higgs field equal to a quadratic differential
![]() $q$
. In this case, the equivalence relation is induced by the action of the unitary gauge group over
$q$
. In this case, the equivalence relation is induced by the action of the unitary gauge group over
![]() $\Sigma \setminus Z$
,
$\Sigma \setminus Z$
,
![]() $Z=q^{-1}(0)$
.
$Z=q^{-1}(0)$
.
There is a natural
![]() $\mathbb{C}^{\ast }$
action on the moduli space
$\mathbb{C}^{\ast }$
action on the moduli space
![]() $\mathcal{M}_{{\rm Hit}}^{{\rm Lim}}$
: Given
$\mathcal{M}_{{\rm Hit}}^{{\rm Lim}}$
: Given
![]() $(A,\phi =\varphi +\varphi ^{\dagger })\in \mathcal{M}_{{\rm Hit}}^{{\rm Lim}}$
and
$(A,\phi =\varphi +\varphi ^{\dagger })\in \mathcal{M}_{{\rm Hit}}^{{\rm Lim}}$
and
![]() $t\in \mathbb{C}^{\ast }$
, we set
$t\in \mathbb{C}^{\ast }$
, we set
![]() $t\cdot [(A,\phi )]=[(A,t\varphi +\bar{t}\varphi ^{\dagger })]$
, which is also a solution to (9).
$t\cdot [(A,\phi )]=[(A,t\varphi +\bar{t}\varphi ^{\dagger })]$
, which is also a solution to (9).
4.2.2 Compactification of the Hitchin moduli space
The following compactness result is due to Taubes [Reference TaubesTau13b] and Mochizuki [Reference MochizukiMoc16] (see also [Reference HeHe20]).
Proposition 4.6.
Let
![]() $(A_{i},\varphi _i)$
be a sequence of solutions to
(5)
, with
$(A_{i},\varphi _i)$
be a sequence of solutions to
(5)
, with
![]() $q_i=\det (\varphi _i)\in H^0(K^2)$
. Then
$q_i=\det (\varphi _i)\in H^0(K^2)$
. Then
-
(i) if
 $\limsup \|q_i\|_{L^2(\Sigma )}\lt \infty$
, then there is a subsequence (also denoted
$\limsup \|q_i\|_{L^2(\Sigma )}\lt \infty$
, then there is a subsequence (also denoted
 $\{i\}$
), a smooth solution
$\{i\}$
), a smooth solution
 $(A_{\infty },\phi _{\infty })$
to
(5)
, and a sequence
$(A_{\infty },\phi _{\infty })$
to
(5)
, and a sequence
 $g_i$
of smooth unitary gauge transformations on
$g_i$
of smooth unitary gauge transformations on
 $\Sigma$
such that
$\Sigma$
such that
 $(A_i,\phi _i)g_i$
converges smoothly to
$(A_i,\phi _i)g_i$
converges smoothly to
 $(A_{\infty },\phi _{\infty })$
on
$(A_{\infty },\phi _{\infty })$
on
 $\Sigma$
;
$\Sigma$
; -
(ii) if
 $\lim \|q_i\|_{L^2(\Sigma )}=\infty$
, then there is a subsequence (also denoted
$\lim \|q_i\|_{L^2(\Sigma )}=\infty$
, then there is a subsequence (also denoted
 $\{i\}$
), and
$\{i\}$
), and
 $q_{\infty }\in H^0(K^2)$
, leading to
over
$q_{\infty }\in H^0(K^2)$
, leading to
over \begin{align*}\frac {q_i}{\Vert q_i\Vert _{L^2}}\longrightarrow q_{\infty }\end{align*}
\begin{align*}\frac {q_i}{\Vert q_i\Vert _{L^2}}\longrightarrow q_{\infty }\end{align*}
 $\Sigma$
, and an admissible solution
$\Sigma$
, and an admissible solution
 $(A_\infty,\phi _{\infty }=\varphi _{\infty }+\varphi ^{\dagger }_{\infty })$
to
(9)
, with
$(A_\infty,\phi _{\infty }=\varphi _{\infty }+\varphi ^{\dagger }_{\infty })$
to
(9)
, with
 $Z_{\infty }:=q_{\infty }^{-1}(0)$
and with smooth unitary gauge transformations
$Z_{\infty }:=q_{\infty }^{-1}(0)$
and with smooth unitary gauge transformations
 $g_i$
on
$g_i$
on
 $\Sigma \setminus Z_\infty$
such that over any open set
$\Sigma \setminus Z_\infty$
such that over any open set
 $ \Omega \Subset \Sigma \setminus Z_{\infty }$
,
$ \Omega \Subset \Sigma \setminus Z_{\infty }$
,
 $(A_i)g_i\to A_\infty$
, and
smoothly on
$(A_i)g_i\to A_\infty$
, and
smoothly on \begin{align*}\frac {g_i^{-1}\phi _ig_i}{\Vert \phi \Vert _{L^2}}\longrightarrow \phi _{\infty }\end{align*}
\begin{align*}\frac {g_i^{-1}\phi _ig_i}{\Vert \phi \Vert _{L^2}}\longrightarrow \phi _{\infty }\end{align*}
 $\Omega$
.
$\Omega$
.
There is also a compactness result for sequences of solutions in
![]() $\mathcal{M}_{{\rm Hit}}^{{\rm Lim}}$
.
$\mathcal{M}_{{\rm Hit}}^{{\rm Lim}}$
.
Proposition 4.7.
Let
![]() $[(A_i,\phi _i=\varphi _i+\varphi _i^{\dagger })]\in \mathcal{M}_{{\rm Hit}}^{{\rm Lim}}$
be a sequence of admissible solutions to
(9)
, and let
$[(A_i,\phi _i=\varphi _i+\varphi _i^{\dagger })]\in \mathcal{M}_{{\rm Hit}}^{{\rm Lim}}$
be a sequence of admissible solutions to
(9)
, and let
![]() $q_i=\det (\varphi _i)$
be the corresponding quadratic differentials. Then, after passing to a subsequence, there are
$q_i=\det (\varphi _i)$
be the corresponding quadratic differentials. Then, after passing to a subsequence, there are
![]() $t_i\in \mathbb{C}^{\ast }$
, a limiting configuration
$t_i\in \mathbb{C}^{\ast }$
, a limiting configuration
![]() $(A_{\infty },\phi _{\infty }=\varphi _{\infty }+\varphi _{\infty }^{\dagger })$
with quadratic differential
$(A_{\infty },\phi _{\infty }=\varphi _{\infty }+\varphi _{\infty }^{\dagger })$
with quadratic differential
![]() $q_{\infty }=\det (\varphi _{\infty })\neq 0$
, and a sequence
$q_{\infty }=\det (\varphi _{\infty })\neq 0$
, and a sequence
![]() $g_i$
of smooth gauge transformations on
$g_i$
of smooth gauge transformations on
![]() $\Sigma \setminus Z_\infty$
, such that:
$\Sigma \setminus Z_\infty$
, such that:
-
(i)
 $t_i^2q_i$
converges smoothly to
$t_i^2q_i$
converges smoothly to
 $q_{\infty }$
and
$q_{\infty }$
and -
(ii) over any open set
 $\Omega \Subset X\setminus Z_{\infty }$
,
$\Omega \Subset X\setminus Z_{\infty }$
,
 $(A_i,t_i\cdot \phi _i)g_i$
converges smoothly to
$(A_i,t_i\cdot \phi _i)g_i$
converges smoothly to
 $(A_{\infty },\phi _{\infty })$
.
$(A_{\infty },\phi _{\infty })$
.
Proof.
Write
![]() $q_i=\det (\varphi _i)\in H^0(K^2)$
. Adjusting by
$q_i=\det (\varphi _i)\in H^0(K^2)$
. Adjusting by
![]() $t_i$
if necessary, we may assume that
$t_i$
if necessary, we may assume that
![]() $q_i$
converges to
$q_i$
converges to
![]() $q_{\infty }$
over
$q_{\infty }$
over
![]() $\Sigma$
. Also, since
$\Sigma$
. Also, since
![]() $F_{A_i}=0$
over
$F_{A_i}=0$
over
![]() $\Sigma \setminus Z_i$
and
$\Sigma \setminus Z_i$
and
![]() $Z_i$
converges to
$Z_i$
converges to
![]() $Z_{\infty }$
, we can apply both Uhlenbeck compactness and the classical bootstrapping method to obtain
$Z_{\infty }$
, we can apply both Uhlenbeck compactness and the classical bootstrapping method to obtain
![]() $A_{\infty }$
such that up to gauge
$A_{\infty }$
such that up to gauge
![]() $A_i$
, it converges smoothly to
$A_i$
, it converges smoothly to
![]() $A_{\infty }$
over
$A_{\infty }$
over
![]() $\Sigma \setminus Z_{\infty }$
. Finally, the convergence of
$\Sigma \setminus Z_{\infty }$
. Finally, the convergence of
![]() $\varphi _i$
follows by the bound on
$\varphi _i$
follows by the bound on
![]() $q_i$
’s.
$q_i$
’s.
4.2.3 The topology on the compactified space
We now carefully define the topology on the space
![]() $\mathcal{M}_{{\rm Hit}} \coprod \mathcal{M}_{{\rm Hit}}^{{\rm Lim}}/\mathbb{C}^{\ast }$
. Choose a metric in the conformal class on
$\mathcal{M}_{{\rm Hit}} \coprod \mathcal{M}_{{\rm Hit}}^{{\rm Lim}}/\mathbb{C}^{\ast }$
. Choose a metric in the conformal class on
![]() $\Sigma$
. Let
$\Sigma$
. Let
![]() $W^{k,2}$
denote the Sobolev spaces on
$W^{k,2}$
denote the Sobolev spaces on
![]() $\Sigma$
of distributional sections with at least
$\Sigma$
of distributional sections with at least
![]() $k$
derivatives in
$k$
derivatives in
![]() $L^2$
. For a finite set of points
$L^2$
. For a finite set of points
![]() $Z \subset \Sigma$
(or indeed any closed subset),
$Z \subset \Sigma$
(or indeed any closed subset),
These definitions extend easily to the space of connections and
![]() $\Omega^1(i \mathfrak{su}(E))$
for a Hermitian vector bundle
$\Omega^1(i \mathfrak{su}(E))$
for a Hermitian vector bundle
![]() $(E,H_0)$
over
$(E,H_0)$
over
![]() $\Sigma$
with a fixed, smooth background connection.
$\Sigma$
with a fixed, smooth background connection.
Let
![]() $\omega _n$
be a nested collection of open sets with
$\omega _n$
be a nested collection of open sets with
![]() $\omega _n\subset \overline{\omega _n} \subset \omega _{n+1}$
and with
$\omega _n\subset \overline{\omega _n} \subset \omega _{n+1}$
and with
![]() $\bigcup _{n}\omega _n= \Sigma \setminus Z$
. We then define the seminorms
$\bigcup _{n}\omega _n= \Sigma \setminus Z$
. We then define the seminorms
![]() $\|f\|_n:=\|f\|_{W^{k,2}(\omega _n)}$
; in terms of these,
$\|f\|_n:=\|f\|_{W^{k,2}(\omega _n)}$
; in terms of these,
![]() $W^{k,2}_{{\rm loc}}(\Sigma \setminus Z)$
is a Fréchet space.
$W^{k,2}_{{\rm loc}}(\Sigma \setminus Z)$
is a Fréchet space.
For any
![]() $q\in H^0(K^2)\setminus \{0\}$
, set
$q\in H^0(K^2)\setminus \{0\}$
, set
![]() $Z_q:=q^{-1}(0)$
, and consider the moduli space
$Z_q:=q^{-1}(0)$
, and consider the moduli space
Here we give a more precise explanation of the above notation. The space
![]() $\mathcal{M}_{{\rm Hit},q^*}$
consists of solutions
$\mathcal{M}_{{\rm Hit},q^*}$
consists of solutions
![]() $(A,\phi =\varphi +\varphi ^{\dagger })$
to the Hitchin equations such that
$(A,\phi =\varphi +\varphi ^{\dagger })$
to the Hitchin equations such that
![]() $\det (\varphi )=tq$
for some nonzero complex number
$\det (\varphi )=tq$
for some nonzero complex number
![]() $t$
. Moreover, the notation
$t$
. Moreover, the notation
![]() $[(A,\phi )]\in \mathcal{M}_{{\rm Hit},q^\ast }\cap W^{k,2}(\Sigma )$
refers to the equivalence class of
$[(A,\phi )]\in \mathcal{M}_{{\rm Hit},q^\ast }\cap W^{k,2}(\Sigma )$
refers to the equivalence class of
![]() $(A,\phi )\in W^{k,2}(\Sigma )$
modulo unitary gauge transformations in
$(A,\phi )\in W^{k,2}(\Sigma )$
modulo unitary gauge transformations in
![]() $W^{k+1,2}(\Sigma )$
. Similarly,
$W^{k+1,2}(\Sigma )$
. Similarly,
![]() $[(A,\phi )]\in \mathcal{M}_{{\rm Hit},q}^{{\rm Lim}}\cap W^{{\rm loc}}$
consists of the equivalence class of
$[(A,\phi )]\in \mathcal{M}_{{\rm Hit},q}^{{\rm Lim}}\cap W^{{\rm loc}}$
consists of the equivalence class of
![]() $(A,\phi )\in W^{k,2}_{{\rm loc}}(\Sigma \setminus Z_q)$
modulo unitary gauge transformations in
$(A,\phi )\in W^{k,2}_{{\rm loc}}(\Sigma \setminus Z_q)$
modulo unitary gauge transformations in
![]() $W^{k+1,2}_{{\rm loc}}(\Sigma \setminus Z_q)$
, and the
$W^{k+1,2}_{{\rm loc}}(\Sigma \setminus Z_q)$
, and the
![]() $\mathbb{C}^{\ast }$
action is given by
$\mathbb{C}^{\ast }$
action is given by
![]() $t\cdot [(A,\phi )]\to [(A,t\phi )].$
By classical bootstrapping of the gauge-theoretic elliptic equations,
$t\cdot [(A,\phi )]\to [(A,t\phi )].$
By classical bootstrapping of the gauge-theoretic elliptic equations,
![]() $\mathbb{M}_q$
is independent of
$\mathbb{M}_q$
is independent of
![]() $k\geq 2$
.
$k\geq 2$
.
Next define
![]() $\mathbb{M}:=\mathcal{M}_{0}\cup \bigcup _{q\in H^0(K^2)\setminus \{0\}}\mathbb{M}_q$
, and based on the definition, we have
$\mathbb{M}:=\mathcal{M}_{0}\cup \bigcup _{q\in H^0(K^2)\setminus \{0\}}\mathbb{M}_q$
, and based on the definition, we have
![]() $\mathbb{M}=\mathcal{M}_{{\rm Hit}}\cup \mathcal{M}_{{\rm Hit}}^{{\rm Lim}}/\mathbb{C}^{\ast }$
. Its topology is generated by two types of open sets. For interior points
$\mathbb{M}=\mathcal{M}_{{\rm Hit}}\cup \mathcal{M}_{{\rm Hit}}^{{\rm Lim}}/\mathbb{C}^{\ast }$
. Its topology is generated by two types of open sets. For interior points
![]() $\xi =[(A,\phi )]\in \mathcal{M}_{{\rm Hit}}\subset \mathbb{M}$
, we use the open sets
$\xi =[(A,\phi )]\in \mathcal{M}_{{\rm Hit}}\subset \mathbb{M}$
, we use the open sets
from the topology of
![]() $\mathcal{M}_{{\rm Hit}}$
. For any boundary point
$\mathcal{M}_{{\rm Hit}}$
. For any boundary point
![]() $\xi _0\in \mathcal{M}_{{\rm Hit}}^{{\rm Lim}}/\mathbb{C}^{\ast }$
, choose a representative
$\xi _0\in \mathcal{M}_{{\rm Hit}}^{{\rm Lim}}/\mathbb{C}^{\ast }$
, choose a representative
![]() $(A_0,\phi _0)$
with
$(A_0,\phi _0)$
with
![]() $\|\phi _0\|_{L^2}=1$
. Let
$\|\phi _0\|_{L^2}=1$
. Let
![]() $q=\det (\phi _0)$
, and fix any open set
$q=\det (\phi _0)$
, and fix any open set
![]() $\omega \Subset \Sigma \setminus Z_q$
. Then, setting
$\omega \Subset \Sigma \setminus Z_q$
. Then, setting
![]() $\mathcal{M}_{{\rm Hit}}^{\ast }=\mathcal{M}_{{\rm Hit}}\setminus \mathcal{H}^{-1}(0)$
,
$\mathcal{M}_{{\rm Hit}}^{\ast }=\mathcal{M}_{{\rm Hit}}\setminus \mathcal{H}^{-1}(0)$
,
 \begin{align*} U_{\xi _0,\omega,\epsilon } & := \Big\{(A,\phi )\in \mathcal{M}_{{\rm Hit}}^{\ast }\mid \|A-A_0\|_{W^{k,2}(\omega )}+\inf _{\theta \in S^1}\|\|\phi \|_{L^2}^{-\frac 12}\phi -e^{i\theta }\phi _0\|_{W^{k,2}(\omega )}\lt \epsilon,\;\|\phi \|_{L^2}\gt {1 \over \epsilon }\Big\}\\& \cup \, \Big\{(A,\phi )\in \mathcal{M}_{{\rm Hit}}^{{\rm Lim}}| \|A-A_0\|_{W^{k,2}(\omega )}+\|\phi -\phi _0\|_{W^{k,2}(\omega )}\lt \epsilon \Big\} \end{align*}
\begin{align*} U_{\xi _0,\omega,\epsilon } & := \Big\{(A,\phi )\in \mathcal{M}_{{\rm Hit}}^{\ast }\mid \|A-A_0\|_{W^{k,2}(\omega )}+\inf _{\theta \in S^1}\|\|\phi \|_{L^2}^{-\frac 12}\phi -e^{i\theta }\phi _0\|_{W^{k,2}(\omega )}\lt \epsilon,\;\|\phi \|_{L^2}\gt {1 \over \epsilon }\Big\}\\& \cup \, \Big\{(A,\phi )\in \mathcal{M}_{{\rm Hit}}^{{\rm Lim}}| \|A-A_0\|_{W^{k,2}(\omega )}+\|\phi -\phi _0\|_{W^{k,2}(\omega )}\lt \epsilon \Big\} \end{align*}
defines an open set around
![]() $\xi _0$
. The sets
$\xi _0$
. The sets
![]() $U_{\xi _0,\omega,\epsilon }$
and
$U_{\xi _0,\omega,\epsilon }$
and
![]() $V_{\xi,\epsilon }$
generate the topology on
$V_{\xi,\epsilon }$
generate the topology on
![]() $\mathbb{M}$
.
$\mathbb{M}$
.
Theorem 4.8.
The space
![]() $\mathbb{M}$
is Hausdorff and compact.
$\mathbb{M}$
is Hausdorff and compact.
Proof.
The Hausdorff property follows from the definition of the topology. By Propositions 4.6 and 4.7,
![]() $\mathbb{M}$
is sequentially compact. Moreover, using this explicit base for the topology,
$\mathbb{M}$
is sequentially compact. Moreover, using this explicit base for the topology,
![]() $\mathbb{M}$
is first countable and, hence, compact.
$\mathbb{M}$
is first countable and, hence, compact.
We may now define the compactification of the Hitchin moduli space as the closure
![]() $\overline{\mathcal{M}}_{{\rm Hit}}\subset \mathbb{M}$
; we write
$\overline{\mathcal{M}}_{{\rm Hit}}\subset \mathbb{M}$
; we write
![]() $\partial \overline{\mathcal{M}}_{{\rm Hit}}$
for the boundary of the closure and
$\partial \overline{\mathcal{M}}_{{\rm Hit}}$
for the boundary of the closure and
![]() $\overline{\mathcal{M}}_{{\rm Hit},q^\ast }:=\overline{\mathcal{M}}_{{\rm Hit}}\cap \mathbb{M}_q$
for the subset of elements with a fixed quadratic differential.
$\overline{\mathcal{M}}_{{\rm Hit},q^\ast }:=\overline{\mathcal{M}}_{{\rm Hit}}\cap \mathbb{M}_q$
for the subset of elements with a fixed quadratic differential.
The following result is described in [Reference Mazzeo, Swoboda, Weiss and WittMSWW16, Reference Ott, Swoboda, Wentworth and WolfOSWW20, Reference Mazzeo, Swoboda, Weiss and WittMSWW19].
Theorem 4.9.
If
![]() $q$
has only simple zeros, then
$q$
has only simple zeros, then
![]() $\overline{\mathcal{M}}_{{\rm Hit},q^\ast }=\mathbb{M}_q$
.
$\overline{\mathcal{M}}_{{\rm Hit},q^\ast }=\mathbb{M}_q$
.
In other words, the compactification of any slice where
![]() $q$
does not lie in the discriminant locus is ‘the obvious one’.
$q$
does not lie in the discriminant locus is ‘the obvious one’.
5. Parabolic modules and stratification of BNR data
In this section, we review the notion of a parabolic module, as described in [Reference RegoReg80, Reference CookCoo93, Reference CookCoo98, Reference Gothen and OliveiraGO13]. This concept leads to a partial normalisation of the generalised Jacobian and Prym varieties of the spectral curve.
5.1 Normalization of the spectral curve
Let
![]() $q\neq 0$
be a quadratic differential with an irreducible, singular spectral curve
$q\neq 0$
be a quadratic differential with an irreducible, singular spectral curve
![]() $S=S_q$
. The zeros of
$S=S_q$
. The zeros of
![]() $q$
define the divisor
$q$
define the divisor
![]() ${\rm Div}(q) = \sum _{i=1}^{r_1} m_i p_i + \sum _{j=1}^{r_2} n_j p^{\prime}_j$
, where the
${\rm Div}(q) = \sum _{i=1}^{r_1} m_i p_i + \sum _{j=1}^{r_2} n_j p^{\prime}_j$
, where the
![]() $m_i$
and
$m_i$
and
![]() $n_j$
are even and odd integers, respectively; and, hence,
$n_j$
are even and odd integers, respectively; and, hence,
![]() $r_1$
and
$r_1$
and
![]() $r_2$
are the numbers of even and odd zeros, respectively, counted without multiplicity. Write
$r_2$
are the numbers of even and odd zeros, respectively, counted without multiplicity. Write
![]() $Z_{{\rm even}} = \{p_1, \dots, p_{r_1}\}$
,
$Z_{{\rm even}} = \{p_1, \dots, p_{r_1}\}$
,
![]() $Z_{{\rm odd}} = \{p^{\prime}_1, \dots, p^{\prime}_{r_2}\}$
and
$Z_{{\rm odd}} = \{p^{\prime}_1, \dots, p^{\prime}_{r_2}\}$
and
![]() $Z = Z_{{\rm even}} \cup Z_{{\rm odd}}$
; so
$Z = Z_{{\rm even}} \cup Z_{{\rm odd}}$
; so
![]() $\#Z=r = r_1 + r_2$
.
$\#Z=r = r_1 + r_2$
.
The map
![]() $\pi : S \to \Sigma$
is a double covering branched along
$\pi : S \to \Sigma$
is a double covering branched along
![]() $Z$
; hence, we may view
$Z$
; hence, we may view
![]() $p_i$
and
$p_i$
and
![]() $p^{\prime}_i$
as points in
$p^{\prime}_i$
as points in
![]() $S$
. For
$S$
. For
![]() $x \in S$
, let
$x \in S$
, let
![]() $\mathcal{O}_x$
be the algebraic local ring,
$\mathcal{O}_x$
be the algebraic local ring,
![]() $\mathcal{O}_x^\ast$
its group of units and
$\mathcal{O}_x^\ast$
its group of units and
![]() $R_x$
the completion. We say that
$R_x$
the completion. We say that
![]() $S$
has an
$S$
has an
![]() $A_n$
singularity at
$A_n$
singularity at
![]() $x$
if
$x$
if
![]() $R_x \cong \mathbb{C}[[r,s]]/(r^2-s^{n+1})$
, where
$R_x \cong \mathbb{C}[[r,s]]/(r^2-s^{n+1})$
, where
![]() $n \geq 1$
. If
$n \geq 1$
. If
![]() $S$
has an
$S$
has an
![]() $A_1$
singularity at
$A_1$
singularity at
![]() $x$
, we call it a nodal singularity, and if
$x$
, we call it a nodal singularity, and if
![]() $S$
has an
$S$
has an
![]() $A_2$
singularity at
$A_2$
singularity at
![]() $x$
, we call it a cusp singularity.
$x$
, we call it a cusp singularity.
Let
![]() $p:\widetilde{S} \to S$
be the normalisation of
$p:\widetilde{S} \to S$
be the normalisation of
![]() $S$
, and let
$S$
, and let
![]() $\tilde{\pi } := \pi \circ p$
:
$\tilde{\pi } := \pi \circ p$
:

For even zeros
![]() $p_i$
, we write
$p_i$
, we write
![]() $p^{-1}(p_i) = \{\tilde{p}_i^{+}, \tilde{p}_i^{-}\}$
, and for odd zeros
$p^{-1}(p_i) = \{\tilde{p}_i^{+}, \tilde{p}_i^{-}\}$
, and for odd zeros
![]() $p^{\prime}_i$
we write
$p^{\prime}_i$
we write
![]() $p^{-1}(p^{\prime}_i) = \tilde{p}^{\prime}_i$
. Since
$p^{-1}(p^{\prime}_i) = \tilde{p}^{\prime}_i$
. Since
![]() $\pi :S\to \Sigma$
is a branched double cover, the involution
$\pi :S\to \Sigma$
is a branched double cover, the involution
![]() $\sigma$
on
$\sigma$
on
![]() $S$
extends to an involution of
$S$
extends to an involution of
![]() $\widetilde{S}$
, which we also denote by
$\widetilde{S}$
, which we also denote by
![]() $\sigma$
. Note that
$\sigma$
. Note that
![]() $\sigma (\tilde{p}^{\prime}_i) = \tilde{p}^{\prime}_i$
while
$\sigma (\tilde{p}^{\prime}_i) = \tilde{p}^{\prime}_i$
while
![]() $\sigma (\tilde{p}_i^\pm ) = \tilde{p}_i^\mp$
.
$\sigma (\tilde{p}_i^\pm ) = \tilde{p}_i^\mp$
.
The ramification divisor
![]() $\Lambda ^{\prime}={1 \over 2}\sum _{i=1}^{r_1}m_ip_i+\frac 12\sum _{j=1}^{r_2}(n_j-1)p^{\prime}_j$
, is a (Weil) divisor on
$\Lambda ^{\prime}={1 \over 2}\sum _{i=1}^{r_1}m_ip_i+\frac 12\sum _{j=1}^{r_2}(n_j-1)p^{\prime}_j$
, is a (Weil) divisor on
![]() $S$
, and there is an exact sequence:
$S$
, and there is an exact sequence:
The genus of
![]() $\widetilde{S}$
is
$\widetilde{S}$
is
![]() $g(\widetilde{S})=4g-3-\deg (\Lambda ^{\prime})=2g-1+r_2/2$
.
$g(\widetilde{S})=4g-3-\deg (\Lambda ^{\prime})=2g-1+r_2/2$
.
5.2 Jacobian under the pull-back to the normalization
We now recall some facts about the Jacobian under the pull-back to the normalization (compare to [Reference Gothen and OliveiraGO13]). Let
![]() $x \in Z \subset S$
be a singular point; that is, either
$x \in Z \subset S$
be a singular point; that is, either
![]() $x\in Z_{{\rm even}}$
or
$x\in Z_{{\rm even}}$
or
![]() $x=p^{\prime}_j$
with
$x=p^{\prime}_j$
with
![]() $n_j\geq 3$
. Let
$n_j\geq 3$
. Let
![]() $\widetilde{\mathcal{O}}_{x}$
be the integral closure of
$\widetilde{\mathcal{O}}_{x}$
be the integral closure of
![]() $\mathcal{O}_x$
. Set
$\mathcal{O}_x$
. Set
![]() $V:=\prod _{x\in Z}\widetilde{\mathcal{O}}_x^{\ast }/\mathcal{O}_x^{\ast }$
. Then we have the following well-known short exact sequence:
$V:=\prod _{x\in Z}\widetilde{\mathcal{O}}_x^{\ast }/\mathcal{O}_x^{\ast }$
. Then we have the following well-known short exact sequence:
This will play an important role later on.
5.2.1 Hitchin fibre
We examine the locally free part
![]() $\mathcal{T}$
of the Hitchin fibre under the pull-back. Here,
$\mathcal{T}$
of the Hitchin fibre under the pull-back. Here,
![]() $\mathcal{T}$
is defined to be the set of
$\mathcal{T}$
is defined to be the set of
![]() $L\in {\rm Pic}^{2g-2}(S)$
such that
$L\in {\rm Pic}^{2g-2}(S)$
such that
![]() $\det (\pi _{\ast }L)=\mathcal{O}_{\Sigma }$
[see (4)]. Although
$\det (\pi _{\ast }L)=\mathcal{O}_{\Sigma }$
[see (4)]. Although
![]() $\Lambda ^{\prime}$
is a divisor
$\Lambda ^{\prime}$
is a divisor
![]() $S$
, it could also be considered to be a divisor on
$S$
, it could also be considered to be a divisor on
![]() $\Sigma$
by the identification of
$\Sigma$
by the identification of
![]() $p_i,p^{\prime}_j$
and
$p_i,p^{\prime}_j$
and
![]() $\pi (p_i), \pi (p^{\prime}_j)$
. To shorten the notation, we write
$\pi (p_i), \pi (p^{\prime}_j)$
. To shorten the notation, we write
![]() $\mathcal{O}_\Sigma (\Lambda ^{\prime})$
for the corresponding line bundle on
$\mathcal{O}_\Sigma (\Lambda ^{\prime})$
for the corresponding line bundle on
![]() $\Sigma$
. For any
$\Sigma$
. For any
![]() $L\in {\rm Pic}(S)$
, from (11) we see that
$L\in {\rm Pic}(S)$
, from (11) we see that
![]() $\det (\tilde{\pi }_{\ast }p^{\ast }L)\cong \det (\pi _{\ast }L)\otimes \mathcal{O}_\Sigma (\Lambda ^{\prime})$
. We define a new set,
$\det (\tilde{\pi }_{\ast }p^{\ast }L)\cong \det (\pi _{\ast }L)\otimes \mathcal{O}_\Sigma (\Lambda ^{\prime})$
. We define a new set,
![]() $\widetilde{\mathcal{T}}$
, as follows:
$\widetilde{\mathcal{T}}$
, as follows:
Then
![]() $p^{\ast }$
maps
$p^{\ast }$
maps
![]() $\mathcal{T}$
to
$\mathcal{T}$
to
![]() $\widetilde{\mathcal{T}}$
. Furthermore, if
$\widetilde{\mathcal{T}}$
. Furthermore, if
![]() $L_1,L_2\in {\rm Pic}(S)$
satisfy
$L_1,L_2\in {\rm Pic}(S)$
satisfy
![]() $p^{\ast }L_1\cong p^{\ast }L_2$
, then we have
$p^{\ast }L_1\cong p^{\ast }L_2$
, then we have
![]() $\pi _{\ast }L_1\cong \pi _{\ast }L_2$
. This means that the fibre of
$\pi _{\ast }L_1\cong \pi _{\ast }L_2$
. This means that the fibre of
![]() $p^{\ast }:{\rm Jac}(S)\to {\rm Jac}(\widetilde{S})$
is the same as that of
$p^{\ast }:{\rm Jac}(S)\to {\rm Jac}(\widetilde{S})$
is the same as that of
![]() $p^{\ast }:\mathcal{T}\to \widetilde{\mathcal{T}}$
, resulting in the following fibration:
$p^{\ast }:\mathcal{T}\to \widetilde{\mathcal{T}}$
, resulting in the following fibration:
5.3 Torsion-free sheaves
Now we present Cook’s parametrisation of rank 1 torsion-free sheaves on curves with Gorenstein singularities (see [Reference CookCoo98, p. 40] and [Reference CookCoo93, Reference RegoReg80]). An explicit computation of the invariants used in this article is provided in Appendix A. Let
![]() $x \in Z$
be a singular point of
$x \in Z$
be a singular point of
![]() $S$
, and let
$S$
, and let
![]() $L\to S$
be a rank 1 torsion-free sheaf. We again let
$L\to S$
be a rank 1 torsion-free sheaf. We again let
![]() $\mathcal{O}_x$
denote the local ring at
$\mathcal{O}_x$
denote the local ring at
![]() $x$
,
$x$
,
![]() $\widetilde{\mathcal{O}}_x$
its integral closure, and
$\widetilde{\mathcal{O}}_x$
its integral closure, and
![]() $\delta _x = \dim _{\mathbb{C}}(\widetilde{\mathcal{O}}_x/\mathcal{O}_x)$
. According to [Reference Greuel and PfisterGP93, Lemma 1.1], there exists a fractional ideal
$\delta _x = \dim _{\mathbb{C}}(\widetilde{\mathcal{O}}_x/\mathcal{O}_x)$
. According to [Reference Greuel and PfisterGP93, Lemma 1.1], there exists a fractional ideal
![]() $I_x$
that is isomorphic to
$I_x$
that is isomorphic to
![]() $L_x$
and uniquely defined up to multiplication by a unit of
$L_x$
and uniquely defined up to multiplication by a unit of
![]() $\widetilde{\mathcal{O}}_x$
such that
$\widetilde{\mathcal{O}}_x$
such that
![]() $\mathcal{O}_x \subset I_x \subset \widetilde{\mathcal{O}}_x$
. We define
$\mathcal{O}_x \subset I_x \subset \widetilde{\mathcal{O}}_x$
. We define
![]() $\ell _x := \dim _{\mathbb{C}} (I_x/\mathcal{O}_x)$
and
$\ell _x := \dim _{\mathbb{C}} (I_x/\mathcal{O}_x)$
and
![]() $b_x:=\dim _{\mathbb{C}}({T}(I_x\otimes _{\mathcal{O}_x}\widetilde{\mathcal{O}}_x))$
, where
$b_x:=\dim _{\mathbb{C}}({T}(I_x\otimes _{\mathcal{O}_x}\widetilde{\mathcal{O}}_x))$
, where
![]() $T$
means the torsion subsheaf. Then
$T$
means the torsion subsheaf. Then
![]() $\ell _x$
and
$\ell _x$
and
![]() $b_x$
are invariants of
$b_x$
are invariants of
![]() $L$
.
$L$
.
Let
![]() $\mathcal{K}_x$
be the field of fractions of
$\mathcal{K}_x$
be the field of fractions of
![]() $\mathcal{O}_x$
. The conductor of
$\mathcal{O}_x$
. The conductor of
![]() $I_x\subset \widetilde{\mathcal{O}}_x$
is defined to be
$I_x\subset \widetilde{\mathcal{O}}_x$
is defined to be
The singularity is characterized by the following dimensions:
 \begin{align} \underbrace{C(\mathcal{O}_x)\subset \overbrace{C(I_x)\subset \overbrace{\mathcal{O}_x\subset \underbrace{I_x\subset \widetilde{\mathcal{O}}_x}_{\delta _x-\ell _x}}^{\delta _x}}^{2\delta _x-2\ell _x}}_{2\delta _x}. \end{align}
\begin{align} \underbrace{C(\mathcal{O}_x)\subset \overbrace{C(I_x)\subset \overbrace{\mathcal{O}_x\subset \underbrace{I_x\subset \widetilde{\mathcal{O}}_x}_{\delta _x-\ell _x}}^{\delta _x}}^{2\delta _x-2\ell _x}}_{2\delta _x}. \end{align}
For
![]() $x = p_i \in Z_{{\rm even}}$
, we have
$x = p_i \in Z_{{\rm even}}$
, we have
![]() $\delta _{p_i}=m_i/2$
, and there are two maximal ideals
$\delta _{p_i}=m_i/2$
, and there are two maximal ideals
![]() $\mathfrak{m}_{\pm }$
in
$\mathfrak{m}_{\pm }$
in
![]() $\widetilde{\mathcal{O}}_x$
corresponding to the points
$\widetilde{\mathcal{O}}_x$
corresponding to the points
![]() $\tilde{p}_i^{\pm }$
. We let
$\tilde{p}_i^{\pm }$
. We let
![]() $(\widetilde{\mathcal{O}}_{p_i}/C(I_{p_i}))_{\mathfrak{m}_{\pm }}$
be the localization by the ideals
$(\widetilde{\mathcal{O}}_{p_i}/C(I_{p_i}))_{\mathfrak{m}_{\pm }}$
be the localization by the ideals
![]() $\mathfrak{m}_{\pm }$
, and we define
$\mathfrak{m}_{\pm }$
, and we define
![]() $a_{\tilde{p}_i^{\pm }}:=\dim _{\mathbb{C}}(\widetilde{\mathcal{O}}_{p_i}/C(I_{p_i}))_{\mathfrak{m}_{\pm }}$
. Moreover, we have
$a_{\tilde{p}_i^{\pm }}:=\dim _{\mathbb{C}}(\widetilde{\mathcal{O}}_{p_i}/C(I_{p_i}))_{\mathfrak{m}_{\pm }}$
. Moreover, we have
![]() $\dim _{\mathbb{C}}(\widetilde{\mathcal{O}}_{p_i}/C(\mathcal{O}_{p_i}))_{\mathfrak{m}_{\pm }}=m_i/2=\delta _{p_i}$
. By Appendix A,
$\dim _{\mathbb{C}}(\widetilde{\mathcal{O}}_{p_i}/C(\mathcal{O}_{p_i}))_{\mathfrak{m}_{\pm }}=m_i/2=\delta _{p_i}$
. By Appendix A,
![]() $a_{\tilde{p}_i^{\pm }}=(m_i/2)-\ell _{p_i}$
, and therefore
$a_{\tilde{p}_i^{\pm }}=(m_i/2)-\ell _{p_i}$
, and therefore
![]() $a_{\tilde{p}_i^+}+a_{\tilde{p}_i^-}=2\delta _{p_i}-2\ell _{p_i}$
and also
$a_{\tilde{p}_i^+}+a_{\tilde{p}_i^-}=2\delta _{p_i}-2\ell _{p_i}$
and also
![]() $b_{p_i}=\ell _{p_i}$
. Define
$b_{p_i}=\ell _{p_i}$
. Define
For
![]() $x=p^{\prime}_i \in Z_{{\rm odd}}$
, we have
$x=p^{\prime}_i \in Z_{{\rm odd}}$
, we have
![]() $\delta _{p^{\prime}_i}=(n_i-1)/2$
, and the maximal ideal
$\delta _{p^{\prime}_i}=(n_i-1)/2$
, and the maximal ideal
![]() $\mathfrak{m}$
of
$\mathfrak{m}$
of
![]() $\widetilde{\mathcal{O}}_x$
is unique. We define
$\widetilde{\mathcal{O}}_x$
is unique. We define
![]() $a_{\tilde{p}^{\prime}_i}:=\dim _{\mathbb{C}}(\widetilde{\mathcal{O}}_{p^{\prime}_i}/C(I_{p^{\prime}_i}))_{\mathfrak{m}}$
. By Appendix A, we have
$a_{\tilde{p}^{\prime}_i}:=\dim _{\mathbb{C}}(\widetilde{\mathcal{O}}_{p^{\prime}_i}/C(I_{p^{\prime}_i}))_{\mathfrak{m}}$
. By Appendix A, we have
![]() $a_{\tilde{p}^{\prime}_i}=2\delta _{p^{\prime}_i}-2\ell _{p^{\prime}_i}$
and
$a_{\tilde{p}^{\prime}_i}=2\delta _{p^{\prime}_i}-2\ell _{p^{\prime}_i}$
and
![]() $b_{p^{\prime}_i}=\ell _{p^{\prime}_i}$
. Moreover,
$b_{p^{\prime}_i}=\ell _{p^{\prime}_i}$
. Moreover,
![]() $\dim _{\mathbb{C}}(\widetilde{\mathcal{O}}_{p^{\prime}_i}/C(\mathcal{O}_{p^{\prime}_i}))_{\mathfrak{m}}=n_i-1=2\delta _{p^{\prime}_i}$
. In this case we set
$\dim _{\mathbb{C}}(\widetilde{\mathcal{O}}_{p^{\prime}_i}/C(\mathcal{O}_{p^{\prime}_i}))_{\mathfrak{m}}=n_i-1=2\delta _{p^{\prime}_i}$
. In this case we set
![]() $V(L_{p^{\prime}_i})=\{\ell _{p^{\prime}_i}\}$
.
$V(L_{p^{\prime}_i})=\{\ell _{p^{\prime}_i}\}$
.
Let
![]() $\eta :\widetilde{\mathcal{O}}_x\to \widetilde{\mathcal{O}}_x/C(\mathcal{O}_x)$
be the quotient map. We define
$\eta :\widetilde{\mathcal{O}}_x\to \widetilde{\mathcal{O}}_x/C(\mathcal{O}_x)$
be the quotient map. We define
Hence, if
![]() $J_x=\eta ^{-1}(F_x)$
with
$J_x=\eta ^{-1}(F_x)$
with
![]() $F_x\in S(L_x)$
, there exists an ideal
$F_x\in S(L_x)$
, there exists an ideal
![]() $\mathfrak{t}_x$
in
$\mathfrak{t}_x$
in
![]() $\widetilde{\mathcal{O}}_x$
such that
$\widetilde{\mathcal{O}}_x$
such that
![]() $J_x=\mathfrak{t}_x\cdot L_x$
. For
$J_x=\mathfrak{t}_x\cdot L_x$
. For
![]() $x=p_i\in Z_{{\rm even}}$
, we obtain two integers:
$x=p_i\in Z_{{\rm even}}$
, we obtain two integers:
![]() $c_{i}^{\pm }=\dim _{\mathbb{C}}(\widetilde{\mathcal{O}}_x/(\mathfrak{t}_x\cdot \widetilde{\mathcal{O}}_x))_{\mathfrak{m}_{\pm }}$
. By [Reference CookCoo98, Lemma 6],
$c_{i}^{\pm }=\dim _{\mathbb{C}}(\widetilde{\mathcal{O}}_x/(\mathfrak{t}_x\cdot \widetilde{\mathcal{O}}_x))_{\mathfrak{m}_{\pm }}$
. By [Reference CookCoo98, Lemma 6],
![]() $(c_i^+,c_i^-)\in V(L_{p_i})$
, for
$(c_i^+,c_i^-)\in V(L_{p_i})$
, for
![]() $x=p^{\prime}_i\in Z_{{\rm odd}}$
and
$x=p^{\prime}_i\in Z_{{\rm odd}}$
and
![]() $\dim _{\mathbb{C}}(\widetilde{\mathcal{O}}_x/(\mathfrak{t}_x\cdot \widetilde{\mathcal{O}}_x))=\ell _{p^{\prime}_i}\in V(L_{p^{\prime}_i})$
, and these only depend only on
$\dim _{\mathbb{C}}(\widetilde{\mathcal{O}}_x/(\mathfrak{t}_x\cdot \widetilde{\mathcal{O}}_x))=\ell _{p^{\prime}_i}\in V(L_{p^{\prime}_i})$
, and these only depend only on
![]() $F_x$
. Hence, there is a well-defined map:
$F_x$
. Hence, there is a well-defined map:
 \begin{align*} \kappa _x:S(L_x)\longrightarrow V(L_x)\ :\ \begin {cases} F_x\to (c_i^+,c_i^-) & \mathrm {when}\;x=p_i,\;\\[3pt] F_x\to \ell _{p^{\prime}_i} & \mathrm {when}\;x=p^{\prime}_i . \end {cases} \end{align*}
\begin{align*} \kappa _x:S(L_x)\longrightarrow V(L_x)\ :\ \begin {cases} F_x\to (c_i^+,c_i^-) & \mathrm {when}\;x=p_i,\;\\[3pt] F_x\to \ell _{p^{\prime}_i} & \mathrm {when}\;x=p^{\prime}_i . \end {cases} \end{align*}
Lemma 5.1.
For
![]() $x\in Z$
, the connected components of
$x\in Z$
, the connected components of
![]() $S(L_x)$
are parameterized by elements in
$S(L_x)$
are parameterized by elements in
![]() $V(L_x)$
.
$V(L_x)$
.
Set
![]() $V(L):=\prod _{x\in Z}V(L_x)$
and
$V(L):=\prod _{x\in Z}V(L_x)$
and
![]() $S(L):=\prod _{x\in Z}S(L_x)$
. Write
$S(L):=\prod _{x\in Z}S(L_x)$
. Write
![]() $N(L) := |V(L)|$
for the number of points in
$N(L) := |V(L)|$
for the number of points in
![]() $V(L)$
. There is a map
$V(L)$
. There is a map
For any
![]() ${\bf c}\in V(L)$
, write
${\bf c}\in V(L)$
, write
![]() ${\bf c}=(c_1^{\pm },\ldots,c_{r_1}^{\pm },\ell _{p^{\prime}_1},\ldots,\ell _{p^{\prime}_{r_2}})$
. Associate to
${\bf c}=(c_1^{\pm },\ldots,c_{r_1}^{\pm },\ell _{p^{\prime}_1},\ldots,\ell _{p^{\prime}_{r_2}})$
. Associate to
![]() ${\bf c}$
the divisor
${\bf c}$
the divisor
 \begin{align*} D_{\mathbf {c}}=\sum _{i=1}^{r_1}(c_i^+\tilde {p}_i^++c_i^-\tilde {p}_i^-)+\sum _{i=1}^{r_2}\ell _{p^{\prime}_i}\tilde {p}^{\prime}_i \end{align*}
\begin{align*} D_{\mathbf {c}}=\sum _{i=1}^{r_1}(c_i^+\tilde {p}_i^++c_i^-\tilde {p}_i^-)+\sum _{i=1}^{r_2}\ell _{p^{\prime}_i}\tilde {p}^{\prime}_i \end{align*}
on
![]() $\widetilde{S}$
. Composing
$\widetilde{S}$
. Composing
![]() $\kappa$
with the map above, we define
$\kappa$
with the map above, we define
The following result is straightforward but important:
Proposition 5.2.
![]() $L$
is locally free if and only if
$L$
is locally free if and only if
![]() $\varkappa=0$
on
$\varkappa=0$
on
![]() $S(L)$
.
$S(L)$
.
Proof.
![]() $L$
is locally free if and only if
$L$
is locally free if and only if
![]() $\ell _x=0$
for all
$\ell _x=0$
for all
![]() $x\in Z$
. The claim then follows directly from the definition of
$x\in Z$
. The claim then follows directly from the definition of
![]() $D_{{\bf c}}$
.
$D_{{\bf c}}$
.
5.4 Parabolic modules
In this subsection, we define the notion of a parabolic module, following [Reference RegoReg80, Reference CookCoo93, Reference CookCoo98]. First note that
![]() $\dim _{\mathbb{C}}(\widetilde{\mathcal{O}}_x/C(\mathcal{O}_x))=2\delta _x$
(compare to (14)). Let
$\dim _{\mathbb{C}}(\widetilde{\mathcal{O}}_x/C(\mathcal{O}_x))=2\delta _x$
(compare to (14)). Let
![]() ${\rm Gr}(\delta _x,\widetilde{\mathcal{O}}_x/C(\mathcal{O}_x))$
be the Grassmannian of
${\rm Gr}(\delta _x,\widetilde{\mathcal{O}}_x/C(\mathcal{O}_x))$
be the Grassmannian of
![]() $\delta _x$
dimensional subspaces of the vector space
$\delta _x$
dimensional subspaces of the vector space
![]() $\widetilde{\mathcal{O}}_x/C(\mathcal{O}_x)$
. Then
$\widetilde{\mathcal{O}}_x/C(\mathcal{O}_x)$
. Then
![]() $\widetilde{\mathcal{O}}^{\ast }_x$
acts on
$\widetilde{\mathcal{O}}^{\ast }_x$
acts on
![]() ${\rm Gr}(\delta _x,\widetilde{\mathcal{O}}_x/C(\mathcal{O}_x))$
by multiplication, with fixed points corresponding to
${\rm Gr}(\delta _x,\widetilde{\mathcal{O}}_x/C(\mathcal{O}_x))$
by multiplication, with fixed points corresponding to
![]() $\delta _x$
-dimensional
$\delta _x$
-dimensional
![]() $\mathcal{O}_x$
submodules of
$\mathcal{O}_x$
submodules of
![]() $\widetilde{\mathcal{O}}_x/C(\mathcal{O}_x)$
. We write
$\widetilde{\mathcal{O}}_x/C(\mathcal{O}_x)$
. We write
![]() $\mathcal{P}(x)$
for the (reduced) variety of fixed points. This is a closed subvariety of
$\mathcal{P}(x)$
for the (reduced) variety of fixed points. This is a closed subvariety of
![]() ${\rm Gr}(\delta _x,\widetilde{\mathcal{O}}_x/C(\mathcal{O}_x))$
.
${\rm Gr}(\delta _x,\widetilde{\mathcal{O}}_x/C(\mathcal{O}_x))$
.
Suppose
![]() $x$
is an
$x$
is an
![]() $A_n$
singularity. For notational convenience, we write
$A_n$
singularity. For notational convenience, we write
![]() $\mathcal{P}(A_n):=\mathcal{P}(x)$
. We have the following:
$\mathcal{P}(A_n):=\mathcal{P}(x)$
. We have the following:
Proposition 5.3. The following holds:
-
(i)
 $\mathcal{P}(A_n)$
is connected and depends only on
$\mathcal{P}(A_n)$
is connected and depends only on
 $\delta _x$
. Also,
$\delta _x$
. Also,
 $\dim _{\mathbb{C}}\mathcal{P}(A_{2n})=n$
, and we have isomorphisms
$\dim _{\mathbb{C}}\mathcal{P}(A_{2n})=n$
, and we have isomorphisms
 $\mathcal{P}(A_{2n-1})\cong \mathcal{P}(A_{2n})$
.
$\mathcal{P}(A_{2n-1})\cong \mathcal{P}(A_{2n})$
. -
(ii) If
 $P(A_0)$
is defined to be a point, then the inclusions
$P(A_0)$
is defined to be a point, then the inclusions
 $\mathcal{P}(A_0)\subset \mathcal{P}(A_2)\subset \cdots \subset \mathcal{P}(A_{2n})$
give a cell decomposition of
$\mathcal{P}(A_0)\subset \mathcal{P}(A_2)\subset \cdots \subset \mathcal{P}(A_{2n})$
give a cell decomposition of
 $\mathcal{P}(A_{2n})$
.
$\mathcal{P}(A_{2n})$
. -
(iii) The singular locus
 ${\rm Sing}(\mathcal{P}(A_{2n}))\cong \mathcal{P}(A_{2n-4})$
. In particular, it has codimension
${\rm Sing}(\mathcal{P}(A_{2n}))\cong \mathcal{P}(A_{2n-4})$
. In particular, it has codimension
 $\geq 2$
. Moreover,
$\geq 2$
. Moreover,
 $\mathcal{P}(A_1)=\mathcal{P}(A_2)\cong \mathbb{C}P^1$
, and
$\mathcal{P}(A_1)=\mathcal{P}(A_2)\cong \mathbb{C}P^1$
, and
 $\mathcal{P}(A_4)$
is a quadric cone.
$\mathcal{P}(A_4)$
is a quadric cone.
Define
![]() $\mathscr{P}(S)=\prod _{x\in Z}\mathcal{P}(x)$
. This depends only on the curve singularity of
$\mathscr{P}(S)=\prod _{x\in Z}\mathcal{P}(x)$
. This depends only on the curve singularity of
![]() $S$
. Let
$S$
. Let
![]() $J\in {\rm Pic}(\widetilde{S})$
. As vector spaces,
$J\in {\rm Pic}(\widetilde{S})$
. As vector spaces,
Definition 5.4.
A parabolic module
![]() ${\rm PMod}(\widetilde{S})$
consists of pairs
${\rm PMod}(\widetilde{S})$
consists of pairs
![]() $(J,v)$
, where
$(J,v)$
, where
![]() $J\in {\rm Jac}(\widetilde{S})$
and
$J\in {\rm Jac}(\widetilde{S})$
and
![]() $v=\prod _{x\in Z} v_x$
, with
$v=\prod _{x\in Z} v_x$
, with
![]() $v_x\in \mathcal{P}(x)$
.
$v_x\in \mathcal{P}(x)$
.
By [Reference CookCoo98, p. 41],
![]() ${\rm PMod}(\widetilde{S})$
has a natural algebraic structure. Let
${\rm PMod}(\widetilde{S})$
has a natural algebraic structure. Let
![]() ${\rm pr}:{\rm PMod}(\widetilde{S})\to {\rm Jac}(\widetilde{S})$
be the projection to the first component. Then
${\rm pr}:{\rm PMod}(\widetilde{S})\to {\rm Jac}(\widetilde{S})$
be the projection to the first component. Then
![]() ${\rm pr}$
defines a fibration of
${\rm pr}$
defines a fibration of
![]() ${\rm PMod}(\widetilde{S})$
with fibre
${\rm PMod}(\widetilde{S})$
with fibre
![]() $\mathscr{P}(S)$
. Moreover, there is a finite morphism
$\mathscr{P}(S)$
. Moreover, there is a finite morphism
![]() $\tau : {\rm PMod}(\widetilde{S})\to \overline{{\rm Jac}}(S)$
defined by sending
$\tau : {\rm PMod}(\widetilde{S})\to \overline{{\rm Jac}}(S)$
defined by sending
![]() $(J,v) \to L$
, where
$(J,v) \to L$
, where
![]() $L$
is given by:
$L$
is given by:
There is a corresponding diagram:

The map
![]() $\tau$
may be regarded as the compactification of the pull-back normalization map
$\tau$
may be regarded as the compactification of the pull-back normalization map
![]() $p^{\ast }$
in (12).
$p^{\ast }$
in (12).
Theorem 5.5 [Reference CookCoo98, Thm. 1].
For the map
![]() $\tau :{\rm PMod}(\widetilde{S})\to \overline{{\rm Jac}}(S)$
defined above,
$\tau :{\rm PMod}(\widetilde{S})\to \overline{{\rm Jac}}(S)$
defined above,
-
(i)
 $\tau$
is a finite morphism, where the fibre over
$\tau$
is a finite morphism, where the fibre over
 $L$
consists of
$L$
consists of
 $N(L)$
points.
$N(L)$
points.
-
(ii) The restriction
 $\tau : \tau ^{-1}{\rm Jac}(S)\to {\rm Jac}(S)$
is an isomorphism. Moreover, for
$\tau : \tau ^{-1}{\rm Jac}(S)\to {\rm Jac}(S)$
is an isomorphism. Moreover, for
 $L\in {\rm Jac}(S)$
, we have
$L\in {\rm Jac}(S)$
, we have
 ${\rm pr}\circ \tau ^{-1}(L)=p^{\ast }(L)$
.
${\rm pr}\circ \tau ^{-1}(L)=p^{\ast }(L)$
. -
(iii) Suppose
 $\tau (J,v)=L$
. For
$\tau (J,v)=L$
. For
 $x\in Z$
, we have
$x\in Z$
, we have
 $v_x\in S(L_x)$
. Let
$v_x\in S(L_x)$
. Let
 $D_{v}=\varkappa (v)$
be the divisor defined in
(15)
. Then
In particular,
$D_{v}=\varkappa (v)$
be the divisor defined in
(15)
. Then
In particular, \begin{align*} 0\longrightarrow p^{\ast }L/{T}(p^{\ast }L)\longrightarrow J\longrightarrow J\otimes \mathcal {O}_{D_v}\longrightarrow 0. \end{align*}
\begin{align*} 0\longrightarrow p^{\ast }L/{T}(p^{\ast }L)\longrightarrow J\longrightarrow J\otimes \mathcal {O}_{D_v}\longrightarrow 0. \end{align*}
 $p^{\ast }L/{T}(p^{\ast }L)=J(-D_v)$
.
$p^{\ast }L/{T}(p^{\ast }L)=J(-D_v)$
.
Suppose that all of the zeros of the quadratic differential
![]() $q$
are odd. Then for
$q$
are odd. Then for
![]() $L\in \overline{{\rm Jac}}(S)$
,
$L\in \overline{{\rm Jac}}(S)$
,
![]() $N(L)=1$
, and we can deduce the following:
$N(L)=1$
, and we can deduce the following:
Corollary 5.6.
If
![]() $q^{-1}(0)=\{p^{\prime}_1,\ldots, p^{\prime}_r\}$
and all zeroes have odd multiplicity, then
$q^{-1}(0)=\{p^{\prime}_1,\ldots, p^{\prime}_r\}$
and all zeroes have odd multiplicity, then
![]() $\tau :{\rm PMod}(\widetilde{S})\to \overline{{\rm Jac}}(S)$
is a bijection. Moreover, for
$\tau :{\rm PMod}(\widetilde{S})\to \overline{{\rm Jac}}(S)$
is a bijection. Moreover, for
![]() $L\in \overline{{\rm Jac}}(S)$
with
$L\in \overline{{\rm Jac}}(S)$
with
![]() $\tau (J,v)=L$
, we have
$\tau (J,v)=L$
, we have
For convenience, we recall the canonical example of a parabolic module.
Example 5.7. Suppose
![]() $q$
contains
$q$
contains
![]() $4g-2$
simple zeros and one zero
$4g-2$
simple zeros and one zero
![]() $x$
of order
$x$
of order
![]() $2$
. Then the spectral curve
$2$
. Then the spectral curve
![]() $S$
has one nodal singularity at
$S$
has one nodal singularity at
![]() $x$
. Denote
$x$
. Denote
![]() $p:\widetilde{S}\to S$
as the normalization, with
$p:\widetilde{S}\to S$
as the normalization, with
![]() $p^{-1}(x)=\{\tilde{x}_+,\tilde{x}_-\}$
. Then
$p^{-1}(x)=\{\tilde{x}_+,\tilde{x}_-\}$
. Then
![]() $\mathscr{P}(S)=\mathbb{C}P^1$
, and we obtain a fibration
$\mathscr{P}(S)=\mathbb{C}P^1$
, and we obtain a fibration
![]() $\mathbb{C}P^1\to {\rm PMod}(\widetilde{S})\to {\rm Jac}(\widetilde{S})$
. Let
$\mathbb{C}P^1\to {\rm PMod}(\widetilde{S})\to {\rm Jac}(\widetilde{S})$
. Let
![]() $L\in \overline{{\rm Jac}}(S)\setminus {\rm Jac}(S)$
. If we write
$L\in \overline{{\rm Jac}}(S)\setminus {\rm Jac}(S)$
. If we write
![]() $\widetilde{L}:=p^{\ast }L/{T}(p^{\ast }L)$
, then
$\widetilde{L}:=p^{\ast }L/{T}(p^{\ast }L)$
, then
We can define two sections:
where
![]() $v_+=[1,0]$
,
$v_+=[1,0]$
,
![]() $v_-=[0,1]$
. Then
$v_-=[0,1]$
. Then
![]() $\overline{{\rm Jac}}(S)$
is the quotient of
$\overline{{\rm Jac}}(S)$
is the quotient of
![]() ${\rm PMod}(\widetilde{S})$
given by the identification
${\rm PMod}(\widetilde{S})$
given by the identification
In particular,
![]() ${\rm PMod}(\widetilde{S})$
is not a fibration over
${\rm PMod}(\widetilde{S})$
is not a fibration over
![]() $\overline{{\rm Jac}}(S)$
.
$\overline{{\rm Jac}}(S)$
.
Proposition 5.8.
The singular set of
![]() ${\rm PMod}(\widetilde{S})$
has codimension at least
${\rm PMod}(\widetilde{S})$
has codimension at least
![]() $2$
. Moreover, if the spectral curve
$2$
. Moreover, if the spectral curve
![]() $S$
contains only cusp or nodal singularities, then
$S$
contains only cusp or nodal singularities, then
![]() ${\rm PMod}(\widetilde{S})$
is smooth.
${\rm PMod}(\widetilde{S})$
is smooth.
Proof.
As the singularities of
![]() ${\rm PMod}(\widetilde{S})$
come from the space
${\rm PMod}(\widetilde{S})$
come from the space
![]() $\mathscr{P}(S)$
, the claim follows from Proposition 5.3.
$\mathscr{P}(S)$
, the claim follows from Proposition 5.3.
Let
![]() $\mathcal{P}:=\{L\in {\rm Jac}(S)\mid \det (\pi _{\ast }L)\cong K^{-1}\}$
and
$\mathcal{P}:=\{L\in {\rm Jac}(S)\mid \det (\pi _{\ast }L)\cong K^{-1}\}$
and
![]() $\overline{\mathcal{P}}$
be the closure of
$\overline{\mathcal{P}}$
be the closure of
![]() $\mathcal{P}$
in
$\mathcal{P}$
in
![]() $\overline{{\rm Pic}}(S)$
. Since we focus on
$\overline{{\rm Pic}}(S)$
. Since we focus on
![]() ${\rm SL}(2,\mathbb{C})$
Higgs bundles, we must consider the parabolic module compactification of the fibration
${\rm SL}(2,\mathbb{C})$
Higgs bundles, we must consider the parabolic module compactification of the fibration
Setting
![]() $\widehat{{\rm PMod}}(\widetilde{S}):=\tau ^{-1}(\overline{\mathcal{P}})$
, there is a diagram from [Reference Gothen and OliveiraGO13, p. 17]
$\widehat{{\rm PMod}}(\widetilde{S}):=\tau ^{-1}(\overline{\mathcal{P}})$
, there is a diagram from [Reference Gothen and OliveiraGO13, p. 17]

Theorem 5.5 proves that
![]() ${\rm pr}\circ \tau ^{-1}|_{\mathcal{P}}=p^{\ast }$
.
${\rm pr}\circ \tau ^{-1}|_{\mathcal{P}}=p^{\ast }$
.
5.5 Stratifications of the BNR data
Recall that
![]() $\overline{\mathcal{T}}$
(resp.
$\overline{\mathcal{T}}$
(resp.
![]() $\overline{\mathcal{P}}$
) is the natural compactification of
$\overline{\mathcal{P}}$
) is the natural compactification of
![]() $\mathcal{T}$
(resp.
$\mathcal{T}$
(resp.
![]() $\mathcal{P}$
) induced by the inclusion
$\mathcal{P}$
) induced by the inclusion
![]() ${\rm Pic}(S)\subset \overline{{\rm Pic}}(S)$
. Parabolic modules define a stratification of
${\rm Pic}(S)\subset \overline{{\rm Pic}}(S)$
. Parabolic modules define a stratification of
![]() $\overline{\mathcal{P}}$
and
$\overline{\mathcal{P}}$
and
![]() $\overline{\mathcal{T}}$
. In the following,
$\overline{\mathcal{T}}$
. In the following,
![]() $\pi :S\to \Sigma$
is a branched double cover,
$\pi :S\to \Sigma$
is a branched double cover,
![]() $\sigma$
is the associated involution on
$\sigma$
is the associated involution on
![]() $S$
, and by
$S$
, and by
![]() $\sigma$
we also denote its extension to an involution on the normalization
$\sigma$
we also denote its extension to an involution on the normalization
![]() $\widetilde{S}$
of
$\widetilde{S}$
of
![]() $S$
.
$S$
.
For a rank 1 torsion-free sheaf
![]() $L\in \overline{{\rm Pic}}(S)$
, consider the map
$L\in \overline{{\rm Pic}}(S)$
, consider the map
that is, the torsion-free part of the pull-back to the normalization. By [Reference RabinowitzRab79],
![]() $p^{\star }_{{\rm tf}}(L)=p^{\ast }L$
at
$p^{\star }_{{\rm tf}}(L)=p^{\ast }L$
at
![]() $x\in \widetilde{S}$
if and only if
$x\in \widetilde{S}$
if and only if
![]() $L$
is locally free at
$L$
is locally free at
![]() $p(x)\in S$
.
$p(x)\in S$
.
Using the previous conventions, recall that we have the divisor
 \begin{align*}\Lambda =\sum _{i=1}^{r_1}\frac {m_i}{2}(\tilde {p}_i^++\tilde {p}_i^-)+\sum _{j=1}^{r_2}n_j\tilde {p}^{\prime}_j\end{align*}
\begin{align*}\Lambda =\sum _{i=1}^{r_1}\frac {m_i}{2}(\tilde {p}_i^++\tilde {p}_i^-)+\sum _{j=1}^{r_2}n_j\tilde {p}^{\prime}_j\end{align*}
on
![]() $\widetilde{S}$
.
$\widetilde{S}$
.
Definition 5.9.
An effective divisor
![]() $D\in {\rm Div}(\widetilde{S})$
is called a
$D\in {\rm Div}(\widetilde{S})$
is called a
![]() $\sigma$
-divisor if
$\sigma$
-divisor if
-
(i)
 $D\leq \Lambda$
and
$D\leq \Lambda$
and
 $\sigma ^{\ast }D=D$
;
$\sigma ^{\ast }D=D$
; -
(ii) and for any
 $x\in {\rm Fix}(\sigma )$
,
$x\in {\rm Fix}(\sigma )$
,
 $D|_x=d_xx$
, where
$D|_x=d_xx$
, where
 $d_x\equiv 0\mod 2$
.
$d_x\equiv 0\mod 2$
.
The
![]() $\sigma$
-divisors play an important role in describing the singular Hitchin fibres.
$\sigma$
-divisors play an important role in describing the singular Hitchin fibres.
Proposition 5.10.
Let
![]() $L\in \overline{\mathcal{P}}$
, and write
$L\in \overline{\mathcal{P}}$
, and write
![]() $\widetilde{L}:=p^{\star }_{{\rm tf}} L$
. Then we have
$\widetilde{L}:=p^{\star }_{{\rm tf}} L$
. Then we have
![]() $\widetilde{L}\otimes \sigma ^{\ast }\widetilde{L}=\mathcal{O}(-D)$
for
$\widetilde{L}\otimes \sigma ^{\ast }\widetilde{L}=\mathcal{O}(-D)$
for
![]() $D$
a
$D$
a
![]() $\sigma$
-divisor.
$\sigma$
-divisor.
For a
![]() $\sigma$
-divisor
$\sigma$
-divisor
![]() $D$
, define
$D$
, define
 \begin{align} \widetilde{\mathcal{T}}_D & =\{J\in {\rm Pic}(\widetilde{S})\mid J\otimes \sigma ^{\ast }J=\mathcal{O}(\Lambda -D)\}\ ; \nonumber\\[3pt] \widetilde{\mathcal{P}}_D & =\{J\in {\rm Pic}(\widetilde{S})\mid J\otimes \sigma ^{\ast }J=\mathcal{O}(-D)\}. \end{align}
\begin{align} \widetilde{\mathcal{T}}_D & =\{J\in {\rm Pic}(\widetilde{S})\mid J\otimes \sigma ^{\ast }J=\mathcal{O}(\Lambda -D)\}\ ; \nonumber\\[3pt] \widetilde{\mathcal{P}}_D & =\{J\in {\rm Pic}(\widetilde{S})\mid J\otimes \sigma ^{\ast }J=\mathcal{O}(-D)\}. \end{align}
By [Reference HornHor22a, Prop. 5.6], when the number of odd zeros
![]() $r_2\gt 0$
or
$r_2\gt 0$
or
![]() $D\neq 0$
,
$D\neq 0$
,
![]() $\widetilde{\mathcal{T}}_D$
and
$\widetilde{\mathcal{T}}_D$
and
![]() $\widetilde{\mathcal{P}}_D$
are abelian torsors over
$\widetilde{\mathcal{P}}_D$
are abelian torsors over
![]() ${\rm Prym}(\widetilde{S}/\Sigma )$
, with dimension
${\rm Prym}(\widetilde{S}/\Sigma )$
, with dimension
![]() $g(\widetilde{S})-g=g-1+\frac 12r_2$
. When
$g(\widetilde{S})-g=g-1+\frac 12r_2$
. When
![]() $r_2=0$
and
$r_2=0$
and
![]() $D=0$
,
$D=0$
,
![]() $\widetilde{\mathcal{P}}_{D}$
and
$\widetilde{\mathcal{P}}_{D}$
and
![]() $\widetilde{\mathcal{T}}_D$
are torsors over
$\widetilde{\mathcal{T}}_D$
are torsors over
![]() ${\rm Nm}^{-1}(\mathcal{O}_{\Sigma })\cup {\rm Nm}^{-1}(I)$
, where
${\rm Nm}^{-1}(\mathcal{O}_{\Sigma })\cup {\rm Nm}^{-1}(I)$
, where
![]() ${\rm Nm}$
is the norm map of the covering
${\rm Nm}$
is the norm map of the covering
![]() $\tilde{\pi }: \tilde{S}\to \Sigma$
, and
$\tilde{\pi }: \tilde{S}\to \Sigma$
, and
![]() $\mathcal{I}$
is the unique non-trivial line bundle that satisfies
$\mathcal{I}$
is the unique non-trivial line bundle that satisfies
![]() $\tilde{\pi }^*\mathcal{I}\cong \mathcal{O}_{\widetilde{S}}$
. In addition, we define
$\tilde{\pi }^*\mathcal{I}\cong \mathcal{O}_{\widetilde{S}}$
. In addition, we define
 \begin{align} \overline{\mathcal{T}}_D & =\{L\in \overline{\mathcal{T}}\mid p^{\star }_{{\rm tf}} L\in \widetilde{\mathcal{T}}_D\}\ ;\nonumber\\[3pt] \overline{\mathcal{P}}_D & =\{L\in \overline{\mathcal{P}}\mid p^{\star }_{{\rm tf}} L\in \widetilde{\mathcal{P}}_D\}. \end{align}
\begin{align} \overline{\mathcal{T}}_D & =\{L\in \overline{\mathcal{T}}\mid p^{\star }_{{\rm tf}} L\in \widetilde{\mathcal{T}}_D\}\ ;\nonumber\\[3pt] \overline{\mathcal{P}}_D & =\{L\in \overline{\mathcal{P}}\mid p^{\star }_{{\rm tf}} L\in \widetilde{\mathcal{P}}_D\}. \end{align}
Then the partial order on divisors defines a stratification of
![]() $\overline{\mathcal{T}}$
(resp.
$\overline{\mathcal{T}}$
(resp.
![]() $\overline{\mathcal{P}}$
) by
$\overline{\mathcal{P}}$
) by
![]() $\cup _{D^{\prime}\leq D}\overline{\mathcal{T}}_{D^{\prime}}$
(resp.
$\cup _{D^{\prime}\leq D}\overline{\mathcal{T}}_{D^{\prime}}$
(resp.
![]() $\cup _{D^{\prime}\leq D}\overline{\mathcal{P}}_{D^{\prime}}$
). The top strata are
$\cup _{D^{\prime}\leq D}\overline{\mathcal{P}}_{D^{\prime}}$
). The top strata are
![]() $\overline{\mathcal{T}}_{D=0}$
(resp.
$\overline{\mathcal{T}}_{D=0}$
(resp.
![]() $\overline{\mathcal{P}}_{D=0}$
), and these consist of the locally free sheaves. From the definition,
$\overline{\mathcal{P}}_{D=0}$
), and these consist of the locally free sheaves. From the definition,
![]() $\mathcal{T}=\overline{\mathcal{T}}_{D=0}$
and
$\mathcal{T}=\overline{\mathcal{T}}_{D=0}$
and
![]() $\mathcal{P}=\overline{\mathcal{P}}_{D=0}$
.
$\mathcal{P}=\overline{\mathcal{P}}_{D=0}$
.
Theorem 5.11.
(i) Suppose
![]() $q$
contains at least one zero of odd order. For each stratum indexed by a
$q$
contains at least one zero of odd order. For each stratum indexed by a
![]() $\sigma$
-divisor
$\sigma$
-divisor
![]() $D$
, if we let
$D$
, if we let
![]() $n_{ss}$
be the number of
$n_{ss}$
be the number of
![]() $p$
such that
$p$
such that
![]() $D|_p=\Lambda |_p$
, then there are holomorphic fibre bundles
$D|_p=\Lambda |_p$
, then there are holomorphic fibre bundles
 \begin{align} & (\mathbb{C}^{\ast })^{k_1}\times \mathbb{C}^{k_2}\longrightarrow \overline{\mathcal{T}}_D\xrightarrow{\hspace{.2cm}p^{\star }_{{\rm tf}}\ } \widetilde{\mathcal{T}}_D\ ;\nonumber\\[3pt]& (\mathbb{C}^{\ast })^{k_1}\times \mathbb{C}^{k_2}\longrightarrow \overline{\mathcal{P}}_D\xrightarrow{\hspace{.2cm}p^{\star }_{{\rm tf}}\ } \widetilde{\mathcal{P}}_D\, \end{align}
\begin{align} & (\mathbb{C}^{\ast })^{k_1}\times \mathbb{C}^{k_2}\longrightarrow \overline{\mathcal{T}}_D\xrightarrow{\hspace{.2cm}p^{\star }_{{\rm tf}}\ } \widetilde{\mathcal{T}}_D\ ;\nonumber\\[3pt]& (\mathbb{C}^{\ast })^{k_1}\times \mathbb{C}^{k_2}\longrightarrow \overline{\mathcal{P}}_D\xrightarrow{\hspace{.2cm}p^{\star }_{{\rm tf}}\ } \widetilde{\mathcal{P}}_D\, \end{align}
where
![]() $k_1=r_1-n_{ss}$
,
$k_1=r_1-n_{ss}$
,
![]() $k_2=2g-2-\frac 12\deg (D)-r_1+n_{ss}-{r_2 \over 2}$
and
$k_2=2g-2-\frac 12\deg (D)-r_1+n_{ss}-{r_2 \over 2}$
and
![]() $r_1,r_2$
are the number of even and odd zeros.
Footnote 1
$r_1,r_2$
are the number of even and odd zeros.
Footnote 1
(ii) Suppose
![]() $q$
is irreducible but all zeros are of even order. Then there exists an analytic space
$q$
is irreducible but all zeros are of even order. Then there exists an analytic space
![]() $\overline{\mathcal{T}}^{\prime}_D$
and a double branched covering
$\overline{\mathcal{T}}^{\prime}_D$
and a double branched covering
![]() $p:\overline{\mathcal{T}}_D\to \overline{\mathcal{T}}^{\prime}_D$
, with
$p:\overline{\mathcal{T}}_D\to \overline{\mathcal{T}}^{\prime}_D$
, with
![]() $\overline{\mathcal{T}}^{\prime}_D$
a holomorphic fibration
$\overline{\mathcal{T}}^{\prime}_D$
a holomorphic fibration
In particular,
![]() $\dim (\overline{\mathcal{P}}_D)=\dim (\overline{\mathcal{T}}_D)=3g-3-\frac 12\deg (D).$
$\dim (\overline{\mathcal{P}}_D)=\dim (\overline{\mathcal{T}}_D)=3g-3-\frac 12\deg (D).$
As explained in [Reference HornHor22a], via the BNR correspondence the stratification above translates into a stratification of the Hitchin fibre. Let
![]() $\chi _{{\rm BNR}}:\overline{\mathcal{T}}\xrightarrow{\sim }\mathcal{M}_q$
be the bijection in Theorem 2.3. Let
$\chi _{{\rm BNR}}:\overline{\mathcal{T}}\xrightarrow{\sim }\mathcal{M}_q$
be the bijection in Theorem 2.3. Let
![]() $D$
be a
$D$
be a
![]() $\sigma$
-divisor. Define
$\sigma$
-divisor. Define
![]() $\mathcal{M}_{q,D}:=\chi _{{\rm BNR}}(\overline{\mathcal{T}}_D)$
. Then the stratification of
$\mathcal{M}_{q,D}:=\chi _{{\rm BNR}}(\overline{\mathcal{T}}_D)$
. Then the stratification of
![]() $\overline{\mathcal{T}}$
induces a stratification on
$\overline{\mathcal{T}}$
induces a stratification on
![]() $\mathcal{M}_q=\bigcup _D\mathcal{M}_{q,D}$
.
$\mathcal{M}_q=\bigcup _D\mathcal{M}_{q,D}$
.
For each
![]() $\sigma$
-divisor
$\sigma$
-divisor
![]() $D$
, since
$D$
, since
![]() $\sigma ^{\ast }D=D$
and for any
$\sigma ^{\ast }D=D$
and for any
![]() $x\in {\rm Fix}(\sigma )$
,
$x\in {\rm Fix}(\sigma )$
,
![]() $D|_x=d_xx$
, where
$D|_x=d_xx$
, where
![]() $d_x\equiv 0\mod 2$
, we can write
$d_x\equiv 0\mod 2$
, we can write
![]() $D^{\prime}:={1 \over 2}\tilde{\pi }(D)$
. Then
$D^{\prime}:={1 \over 2}\tilde{\pi }(D)$
. Then
![]() $D^{\prime}$
is an effective divisor with
$D^{\prime}$
is an effective divisor with
![]() ${\rm supp\;} D^{\prime}\subset Z$
. Moreover, for
${\rm supp\;} D^{\prime}\subset Z$
. Moreover, for
![]() $x\in q^{-1}(0)$
,
$x\in q^{-1}(0)$
,
![]() $D^{\prime}_x\leq \frac 12\lfloor {\rm ord}_x(q) \rfloor$
. Therefore,
$D^{\prime}_x\leq \frac 12\lfloor {\rm ord}_x(q) \rfloor$
. Therefore,
![]() $\mathcal{M}_q$
may be regarded as also being stratified by divisors
$\mathcal{M}_q$
may be regarded as also being stratified by divisors
![]() $D^{\prime}$
defined over
$D^{\prime}$
defined over
![]() $\Sigma$
.
$\Sigma$
.
5.6 The structure of the parabolic module projection
We now explain the relationship between the divisor
![]() $D_v$
in Theorem 5.5 and the
$D_v$
in Theorem 5.5 and the
![]() $\sigma$
-divisor. Given
$\sigma$
-divisor. Given
![]() $L \in \overline{\mathcal{P}}$
, define
$L \in \overline{\mathcal{P}}$
, define
 \begin{align} \mathscr{N}_L & :=\{(J,v)\in \widehat{{\rm PMod}}(\widetilde{S})\mid \tau (J,v)=L\}\ ;\nonumber\\ \mathscr{D}_L & :=\{D_v\mid (J,v)\in \mathscr{N}_L\}\, \end{align}
\begin{align} \mathscr{N}_L & :=\{(J,v)\in \widehat{{\rm PMod}}(\widetilde{S})\mid \tau (J,v)=L\}\ ;\nonumber\\ \mathscr{D}_L & :=\{D_v\mid (J,v)\in \mathscr{N}_L\}\, \end{align}
That is,
![]() $\mathscr{N}_L=\tau ^{-1}(L)$
, and
$\mathscr{N}_L=\tau ^{-1}(L)$
, and
![]() $\mathscr{D}_L$
is the collection of divisors
$\mathscr{D}_L$
is the collection of divisors
![]() $D_v$
such that
$D_v$
such that
![]() $J(-D_v) = p^{\star }_{{\rm tf}}(L)$
. By Theorem 5.5, if
$J(-D_v) = p^{\star }_{{\rm tf}}(L)$
. By Theorem 5.5, if
![]() $\tau (J, v) = \tau (J^{\prime}, v)$
, then
$\tau (J, v) = \tau (J^{\prime}, v)$
, then
![]() $J^{\prime} = J(D_{v^{\prime}} - D_v)$
. By (16), as
$J^{\prime} = J(D_{v^{\prime}} - D_v)$
. By (16), as
![]() $L\in \overline{\mathcal{P}}$
, we have
$L\in \overline{\mathcal{P}}$
, we have
![]() $J,J^{\prime}\in {\rm Prym}(\widetilde{S}/\Sigma )$
, which implies
$J,J^{\prime}\in {\rm Prym}(\widetilde{S}/\Sigma )$
, which implies
![]() $D_v=D_{v^{\prime}}$
. Therefore, for the cardinalities, we have
$D_v=D_{v^{\prime}}$
. Therefore, for the cardinalities, we have
![]() $|\mathscr{N}_L|=|\mathscr{D}_L|$
. Furthermore, we define
$|\mathscr{N}_L|=|\mathscr{D}_L|$
. Furthermore, we define
![]() $N_L:=| \mathscr{N}_L|=|\mathscr{D}_L|$
.
$N_L:=| \mathscr{N}_L|=|\mathscr{D}_L|$
.
The divisor
![]() $D_v$
satisfies the following symmetry proposition:
$D_v$
satisfies the following symmetry proposition:
Proposition 5.12.
Let
![]() $D$
be a
$D$
be a
![]() $\sigma$
-divisor and
$\sigma$
-divisor and
![]() $L \in \overline{\mathcal{P}}_D$
. For any
$L \in \overline{\mathcal{P}}_D$
. For any
![]() $D_v \in \mathscr{D}_L$
, we have
$D_v \in \mathscr{D}_L$
, we have
![]() $D_v + \sigma ^{\ast } D_v = D$
.
$D_v + \sigma ^{\ast } D_v = D$
.
Proof.
Let
![]() $\tau (J, v) = L$
. Then by Theorem 5.5, we have
$\tau (J, v) = L$
. Then by Theorem 5.5, we have
![]() $\widetilde{L} = J(-D_v)$
, where
$\widetilde{L} = J(-D_v)$
, where
![]() $\widetilde{L} = p^{\star }_{{\rm tf}}(L)$
. As
$\widetilde{L} = p^{\star }_{{\rm tf}}(L)$
. As
![]() $L \in \overline{\mathcal{P}}_D$
and
$L \in \overline{\mathcal{P}}_D$
and
![]() $J \in {\rm Prym}(\widetilde{S}/\Sigma )$
, we have
$J \in {\rm Prym}(\widetilde{S}/\Sigma )$
, we have
![]() $\widetilde{L} \otimes \sigma ^{\ast } \widetilde{L} = \mathcal{O}(-D)$
and
$\widetilde{L} \otimes \sigma ^{\ast } \widetilde{L} = \mathcal{O}(-D)$
and
![]() $J \otimes \sigma ^{\ast } J = \mathcal{O}_{\widetilde{S}}$
, which implies
$J \otimes \sigma ^{\ast } J = \mathcal{O}_{\widetilde{S}}$
, which implies
![]() $D_v + \sigma ^{\ast } D_v = D$
.
$D_v + \sigma ^{\ast } D_v = D$
.
As a consequence, we have the following:
Corollary 5.13.
Suppose
![]() $q$
has only zeros of odd order. Then for
$q$
has only zeros of odd order. Then for
![]() $L \in \overline{\mathcal{P}}_D$
and
$L \in \overline{\mathcal{P}}_D$
and
![]() $D_v \in \mathscr{D}_L$
, we have
$D_v \in \mathscr{D}_L$
, we have
![]() $\sigma ^{\ast } D_v = D_v$
and
$\sigma ^{\ast } D_v = D_v$
and
![]() $D_v = {1 \over 2}D$
. In addition,
$D_v = {1 \over 2}D$
. In addition,
![]() $\tau : \widehat{{\rm PMod}}(\widetilde{S}) \to \overline{\mathcal{P}}$
is a bijection.
$\tau : \widehat{{\rm PMod}}(\widetilde{S}) \to \overline{\mathcal{P}}$
is a bijection.
Proof.
Since each zero has odd order,
![]() ${\rm supp\;}(D_v) \subset {\rm Fix}(\sigma )$
, which implies
${\rm supp\;}(D_v) \subset {\rm Fix}(\sigma )$
, which implies
![]() $D_v = \sigma ^{\ast } D_v$
. By Proposition 5.12, we must have
$D_v = \sigma ^{\ast } D_v$
. By Proposition 5.12, we must have
![]() $D_v = {1 \over 2}D$
.
$D_v = {1 \over 2}D$
.
There are relationships among the integers appearing in the construction of the parabolic module.
Lemma 5.14.
Let
![]() $D=\sum _{i=1}^{r_1} d_i(\tilde{p}_i^+ + \tilde{p}_i^-) + \sum _{i=1}^{r_2} d^{\prime}_{i}\tilde{p}^{\prime}_i$
be a
$D=\sum _{i=1}^{r_1} d_i(\tilde{p}_i^+ + \tilde{p}_i^-) + \sum _{i=1}^{r_2} d^{\prime}_{i}\tilde{p}^{\prime}_i$
be a
![]() $\sigma$
-divisor, and let
$\sigma$
-divisor, and let
![]() $L\in \overline{\mathcal{P}}_D$
. Then we have
$L\in \overline{\mathcal{P}}_D$
. Then we have
-
(i)
 $\ell _{p_i}=d_i$
and
$\ell _{p_i}=d_i$
and
 $\ell _{p^{\prime}_i}=d^{\prime}_i/2$
;
$\ell _{p^{\prime}_i}=d^{\prime}_i/2$
; -
(ii)
 $a_{\tilde{p}_i^+}=a_{\tilde{p}_i^-}=(m_i/2)-d_i$
and
$a_{\tilde{p}_i^+}=a_{\tilde{p}_i^-}=(m_i/2)-d_i$
and
 $a_{\tilde{p}^{\prime}_i}=n_i-1-d^{\prime}_i$
.
$a_{\tilde{p}^{\prime}_i}=n_i-1-d^{\prime}_i$
.
Proof.
Since
![]() $L\in \overline{\mathcal{P}}_D$
, we have
$L\in \overline{\mathcal{P}}_D$
, we have
![]() $\dim{T}(p^{\ast }L_{p_i})=d_i$
and
$\dim{T}(p^{\ast }L_{p_i})=d_i$
and
![]() $\dim{T}(p^{\ast }L_{p^{\prime}_i})=d^{\prime}_i/2$
. The claim then follows from Proposition 9.2.1.
$\dim{T}(p^{\ast }L_{p^{\prime}_i})=d^{\prime}_i/2$
. The claim then follows from Proposition 9.2.1.
Proposition 5.15.
Let
![]() $D=\sum _{i=1}^{r_1} d_i(\tilde{p}_i^+ + \tilde{p}_i^-) + \sum _{i=1}^{r_2} d^{\prime}_{i}\tilde{p}^{\prime}_i$
be a
$D=\sum _{i=1}^{r_1} d_i(\tilde{p}_i^+ + \tilde{p}_i^-) + \sum _{i=1}^{r_2} d^{\prime}_{i}\tilde{p}^{\prime}_i$
be a
![]() $\sigma$
-divisor, and let
$\sigma$
-divisor, and let
![]() $L\in \overline{\mathcal{P}}_D$
. Then
$L\in \overline{\mathcal{P}}_D$
. Then
![]() $N_L=\prod _{i=1}^{r_1}(d_i+1)$
. The number
$N_L=\prod _{i=1}^{r_1}(d_i+1)$
. The number
![]() $N_L$
depends only on the
$N_L$
depends only on the
![]() $\sigma$
-divisor
$\sigma$
-divisor
![]() $D$
.
$D$
.
Proof.
By Lemma 5.14,
![]() $V(L)$
can be rewritten as
$V(L)$
can be rewritten as
If we define
![]() $n_L$
to be the number of
$n_L$
to be the number of
![]() $D_v\in \mathscr{D}_L$
such that
$D_v\in \mathscr{D}_L$
such that
![]() $\sigma ^{\ast }D_v\neq D_v$
, then we have the following:
$\sigma ^{\ast }D_v\neq D_v$
, then we have the following:
Proposition 5.16
-
(i)
 $n_L$
is even;
$n_L$
is even;
-
(ii) if
 $L\in \overline{\mathcal{P}}_D$
with
and if there exists
$L\in \overline{\mathcal{P}}_D$
with
and if there exists \begin{align*} D=\sum _{i=1}^{r_1}d_i(\tilde {p}_i^++\tilde {p}_i^-)+\sum _{i=1}^{r_2}d^{\prime}_{i}\tilde {p}^{\prime}_i\,\end{align*}
\begin{align*} D=\sum _{i=1}^{r_1}d_i(\tilde {p}_i^++\tilde {p}_i^-)+\sum _{i=1}^{r_2}d^{\prime}_{i}\tilde {p}^{\prime}_i\,\end{align*}
 $i_0\in \{1,\dots,r_1\}$
such that
$i_0\in \{1,\dots,r_1\}$
such that
 $d_{i_0}$
is not even, then
$d_{i_0}$
is not even, then
 $n_L=N_L$
; otherwise,
$n_L=N_L$
; otherwise,
 $n_L=N_L-1$
.
$n_L=N_L-1$
.
Proof.
To prove (i), note that if
![]() $\sigma ^{\ast }D_v\neq D_v$
, then
$\sigma ^{\ast }D_v\neq D_v$
, then
![]() $\sigma ^{\ast }(\sigma ^{\ast }D_v)\neq \sigma ^{\ast }D_v$
, which means that
$\sigma ^{\ast }(\sigma ^{\ast }D_v)\neq \sigma ^{\ast }D_v$
, which means that
![]() $n_L$
is even. For (ii), by Proposition 5.15,
$n_L$
is even. For (ii), by Proposition 5.15,
![]() $D_v=\sigma ^{\ast }D_v$
for
$D_v=\sigma ^{\ast }D_v$
for
![]() $D_v\in \mathscr{D}_L$
if and only if
$D_v\in \mathscr{D}_L$
if and only if
![]() $c_{i}^+=c_i^-=d_i/2$
. Therefore,
$c_{i}^+=c_i^-=d_i/2$
. Therefore,
![]() $n_L\neq N_L$
if and only if all
$n_L\neq N_L$
if and only if all
![]() $d_i$
are even, which implies (ii).
$d_i$
are even, which implies (ii).
We should note that the integer
![]() $n_L$
depends only on the Higgs divisor
$n_L$
depends only on the Higgs divisor
![]() $D$
, and in the rest of this article, we define
$D$
, and in the rest of this article, we define
![]() $n_D:={n_L \over 2}.$
$n_D:={n_L \over 2}.$
6. Irreducible singular fibres and the Mochizuki map
In this section, we provide a reinterpretation of the limiting configuration construction of a Higgs bundle on an irreducible fibre, as introduced by Mochizuki in [Reference MochizukiMoc16] (see also [Reference HornHor22a]). We also investigate the relationship between limiting configurations and the stratification.
6.1 Abelianization of a Higgs bundle
Let
![]() $q$
be a fixed irreducible quadratic differential with spectral curve
$q$
be a fixed irreducible quadratic differential with spectral curve
![]() $S$
and with normalisation
$S$
and with normalisation
![]() $p:\widetilde{S}\to S$
. We define
$p:\widetilde{S}\to S$
. We define
![]() $\widetilde{K}:=\widetilde{\pi }^{\ast }K$
(but note that
$\widetilde{K}:=\widetilde{\pi }^{\ast }K$
(but note that
![]() $\widetilde{K}\neq K_{\widetilde S}$
) and
$\widetilde{K}\neq K_{\widetilde S}$
) and
![]() $\widetilde{q}:=\widetilde{\pi }^{\ast }q\in H^0(\widetilde{K}^2)$
, where
$\widetilde{q}:=\widetilde{\pi }^{\ast }q\in H^0(\widetilde{K}^2)$
, where
![]() $\widetilde{\pi }$
is as in (10). Choose a square root
$\widetilde{\pi }$
is as in (10). Choose a square root
![]() $\omega \in H^0(\widetilde{K})$
such that
$\omega \in H^0(\widetilde{K})$
such that
![]() $\widetilde{q}=-\omega \otimes \omega$
(that is,
$\widetilde{q}=-\omega \otimes \omega$
(that is,
![]() $\omega =p^\ast \lambda$
). Let
$\omega =p^\ast \lambda$
). Let
![]() $\Lambda :={\rm Div}(\omega )$
and
$\Lambda :={\rm Div}(\omega )$
and
![]() $\widetilde{Z}:={\rm supp}(\Lambda )$
. We can then write
$\widetilde{Z}:={\rm supp}(\Lambda )$
. We can then write
 \begin{align} \Lambda =\sum _{i=1}^{r_1}{m_i \over 2}(\tilde{p}_i^++\tilde{p}_i^-)+\sum _{j=1}^{r_2}n_j\tilde{p}^{\prime}_j. \end{align}
\begin{align} \Lambda =\sum _{i=1}^{r_1}{m_i \over 2}(\tilde{p}_i^++\tilde{p}_i^-)+\sum _{j=1}^{r_2}n_j\tilde{p}^{\prime}_j. \end{align}
If
![]() $\sigma :\widetilde{S}\to \widetilde{S}$
denotes the involution, then
$\sigma :\widetilde{S}\to \widetilde{S}$
denotes the involution, then
![]() $\sigma ^{\ast }\omega =-\omega$
.
$\sigma ^{\ast }\omega =-\omega$
.
Let
![]() $(\mathcal{E},\varphi )$
be a Higgs bundle on
$(\mathcal{E},\varphi )$
be a Higgs bundle on
![]() $\Sigma$
with
$\Sigma$
with
![]() $\det \varphi =q$
. Consider the pull-back
$\det \varphi =q$
. Consider the pull-back
![]() $(\widetilde{\mathcal{E}},\tilde{\varphi }):=(\widetilde{\pi }^{\ast }\mathcal{E},\widetilde{\pi }^{\ast }\varphi )$
to
$(\widetilde{\mathcal{E}},\tilde{\varphi }):=(\widetilde{\pi }^{\ast }\mathcal{E},\widetilde{\pi }^{\ast }\varphi )$
to
![]() $\widetilde S$
. We have
$\widetilde S$
. We have
![]() $\tilde{\varphi }\in H^0({\rm End}(\widetilde{\mathcal{E}})\otimes \widetilde{K})$
and
$\tilde{\varphi }\in H^0({\rm End}(\widetilde{\mathcal{E}})\otimes \widetilde{K})$
and
![]() $\widetilde{q}=\det (\tilde{\varphi })$
. Since
$\widetilde{q}=\det (\tilde{\varphi })$
. Since
![]() $\widetilde{q}=-\omega \otimes \omega$
,
$\widetilde{q}=-\omega \otimes \omega$
,
![]() $\pm \omega$
are well-defined eigenvalues of
$\pm \omega$
are well-defined eigenvalues of
![]() $\tilde{\varphi }$
over
$\tilde{\varphi }$
over
![]() $\widetilde{S}$
. Let
$\widetilde{S}$
. Let
![]() $\tilde{\lambda }$
be the canonical section of the pull-back of
$\tilde{\lambda }$
be the canonical section of the pull-back of
![]() $\widetilde K$
to the total space
$\widetilde K$
to the total space
![]() ${\rm Tot}(\widetilde{K})$
. The spectral curve for
${\rm Tot}(\widetilde{K})$
. The spectral curve for
![]() $(\widetilde{\mathcal{E}},\tilde{\varphi })$
is defined by the equation
$(\widetilde{\mathcal{E}},\tilde{\varphi })$
is defined by the equation
The set
![]() $\widetilde{S}^{\prime}={\rm Im}(\omega )\cup {\rm Im}(-\omega )\subset {\rm Tot}(\widetilde{K})$
decomposes into two irreducible pieces:
$\widetilde{S}^{\prime}={\rm Im}(\omega )\cup {\rm Im}(-\omega )\subset {\rm Tot}(\widetilde{K})$
decomposes into two irreducible pieces:
Having fixed a choice of
![]() $\omega$
, the eigenvalues of
$\omega$
, the eigenvalues of
![]() $\tilde{\varphi }$
are globally well-defined, and we can define the line bundle
$\tilde{\varphi }$
are globally well-defined, and we can define the line bundle
![]() $\widetilde{L}_+\subset \widetilde{\mathcal{E}}$
as
$\widetilde{L}_+\subset \widetilde{\mathcal{E}}$
as
![]() $\widetilde{L}_+:=\ker (\tilde{\varphi }-\omega )$
. Since
$\widetilde{L}_+:=\ker (\tilde{\varphi }-\omega )$
. Since
![]() $\sigma ^{\ast }\omega =-\omega$
,
$\sigma ^{\ast }\omega =-\omega$
,
![]() $\widetilde{L}_-=\sigma ^{\ast }\widetilde{L}_+=\ker (\tilde{\varphi }+\omega )$
, and there is an isomorphism
$\widetilde{L}_-=\sigma ^{\ast }\widetilde{L}_+=\ker (\tilde{\varphi }+\omega )$
, and there is an isomorphism
![]() $\widetilde{\mathcal{E}}|_{\widetilde{S}\setminus \widetilde{Z}}\cong \widetilde{L}_+\oplus \widetilde{L}_-|_{\widetilde{S}\setminus \widetilde{Z}}$
.
$\widetilde{\mathcal{E}}|_{\widetilde{S}\setminus \widetilde{Z}}\cong \widetilde{L}_+\oplus \widetilde{L}_-|_{\widetilde{S}\setminus \widetilde{Z}}$
.
There is also a local description of
![]() $(\widetilde{\mathcal{E}},\tilde{\varphi })$
.
$(\widetilde{\mathcal{E}},\tilde{\varphi })$
.
Lemma 6.1.
Let
![]() $x\in \widetilde{Z}$
and write
$x\in \widetilde{Z}$
and write
![]() $\Lambda |_x=m_xx$
. Let
$\Lambda |_x=m_xx$
. Let
![]() $U$
be a holomorphic coordinate neighborhood of
$U$
be a holomorphic coordinate neighborhood of
![]() $x$
. Then there exists a frame
$x$
. Then there exists a frame
![]() $\mathfrak{e}\in H^0(U,\widetilde{K})$
such that, under a suitable trivialization of
$\mathfrak{e}\in H^0(U,\widetilde{K})$
such that, under a suitable trivialization of
![]() $\mathcal{E}|_U\cong U\times \mathbb{C}^2$
, we can write
$\mathcal{E}|_U\cong U\times \mathbb{C}^2$
, we can write
 \begin{align} \tilde{\varphi }=z^{d_x}\left(\begin{array}{c@{\quad}c} 0 & 1\\[4pt] z^{2m_x-2d_x} & 0 \end{array}\right) \otimes \mathfrak{e}. \end{align}
\begin{align} \tilde{\varphi }=z^{d_x}\left(\begin{array}{c@{\quad}c} 0 & 1\\[4pt] z^{2m_x-2d_x} & 0 \end{array}\right) \otimes \mathfrak{e}. \end{align}
Moreover, if we define
![]() $D:=\sum _{x\in \widetilde{Z}}d_xx$
, then
$D:=\sum _{x\in \widetilde{Z}}d_xx$
, then
![]() $D$
is a
$D$
is a
![]() $\sigma$
-divisor.
$\sigma$
-divisor.
Lemma 6.2.
For the
![]() $\widetilde{L}_{\pm }$
defined above, we have
$\widetilde{L}_{\pm }$
defined above, we have
![]() $\widetilde{L}_+\otimes \widetilde{L}_-=\mathcal{O}_{\widetilde S}(D-\Lambda )$
. Moreover, if we denote
$\widetilde{L}_+\otimes \widetilde{L}_-=\mathcal{O}_{\widetilde S}(D-\Lambda )$
. Moreover, if we denote
![]() $\widetilde{L}_0:=\widetilde{L}_+(\Lambda -D)$
and
$\widetilde{L}_0:=\widetilde{L}_+(\Lambda -D)$
and
![]() $\widetilde{L}_1:=\sigma ^{\ast }\widetilde{L}_0$
, then
$\widetilde{L}_1:=\sigma ^{\ast }\widetilde{L}_0$
, then
![]() $\widetilde{L}_+=\widetilde{\mathcal{E}}\cap \widetilde{L}_0$
,
$\widetilde{L}_+=\widetilde{\mathcal{E}}\cap \widetilde{L}_0$
,
![]() $\widetilde{L}_-=\widetilde{\mathcal{E}}\cap \widetilde{L}_1$
, and we have the exact sequences
$\widetilde{L}_-=\widetilde{\mathcal{E}}\cap \widetilde{L}_1$
, and we have the exact sequences
 \begin{align*} 0\longrightarrow \widetilde{L}_+\longrightarrow \widetilde{\mathcal{E}} \longrightarrow \widetilde{L}_1\longrightarrow 0\ ;\\ 0\longrightarrow \widetilde{L}_-\longrightarrow \widetilde{\mathcal{E}} \longrightarrow \widetilde{L}_0\longrightarrow 0. \end{align*}
\begin{align*} 0\longrightarrow \widetilde{L}_+\longrightarrow \widetilde{\mathcal{E}} \longrightarrow \widetilde{L}_1\longrightarrow 0\ ;\\ 0\longrightarrow \widetilde{L}_-\longrightarrow \widetilde{\mathcal{E}} \longrightarrow \widetilde{L}_0\longrightarrow 0. \end{align*}
Proof.
The inclusion of
![]() $\widetilde{L}_{\pm }\to \widetilde{\mathcal{E}}$
defines an exact sequence:
$\widetilde{L}_{\pm }\to \widetilde{\mathcal{E}}$
defines an exact sequence:
where
![]() $\mathcal{T}$
is a torsion sheaf with
$\mathcal{T}$
is a torsion sheaf with
![]() ${\rm supp\;} \mathcal{T}\subset \widetilde{Z}$
. From the local description in (22), in the same trivialization,
${\rm supp\;} \mathcal{T}\subset \widetilde{Z}$
. From the local description in (22), in the same trivialization,
![]() $\widetilde{L}_{\pm }$
are spanned by the bases
$\widetilde{L}_{\pm }$
are spanned by the bases
![]() $s_{\pm }=\binom{1}{\pm z^{m_x-d_x}}.$
Therefore, as
$s_{\pm }=\binom{1}{\pm z^{m_x-d_x}}.$
Therefore, as
![]() $\det (\mathcal{E})=\mathcal{O}_\Sigma$
, we obtain
$\det (\mathcal{E})=\mathcal{O}_\Sigma$
, we obtain
![]() $\widetilde{L}_+\otimes \widetilde{L}_-=\mathcal{O}_{\widetilde S}(D-\Lambda )$
. Since
$\widetilde{L}_+\otimes \widetilde{L}_-=\mathcal{O}_{\widetilde S}(D-\Lambda )$
. Since
![]() $s_+,s_-$
are linear independent away from
$s_+,s_-$
are linear independent away from
![]() $z$
,
$z$
,
![]() $\widetilde{\mathcal{E}}/\widetilde{L}_+$
is locally generated by the section
$\widetilde{\mathcal{E}}/\widetilde{L}_+$
is locally generated by the section
![]() $z^{d_x-m_x}s_-$
. Therefore,
$z^{d_x-m_x}s_-$
. Therefore,
![]() $\widetilde{\mathcal{E}}/\widetilde{L}_+\cong \widetilde{L}_-(\Lambda -D)=\widetilde{L}_1$
. Using the involution, we obtain the other exact sequence.
$\widetilde{\mathcal{E}}/\widetilde{L}_+\cong \widetilde{L}_-(\Lambda -D)=\widetilde{L}_1$
. Using the involution, we obtain the other exact sequence.
Therefore, if
![]() $\widetilde{L}\otimes \sigma ^{\ast }\widetilde{L}=\mathcal{O}_{\widetilde S}(D-\Lambda )$
, we have
$\widetilde{L}\otimes \sigma ^{\ast }\widetilde{L}=\mathcal{O}_{\widetilde S}(D-\Lambda )$
, we have
![]() $\widetilde{L}_0=\widetilde{L}(\Lambda -D)\in \widetilde{\mathcal{T}}_D$
. In summary, the construction above leads us to consider the composition of the following maps given by the composition
$\widetilde{L}_0=\widetilde{L}(\Lambda -D)\in \widetilde{\mathcal{T}}_D$
. In summary, the construction above leads us to consider the composition of the following maps given by the composition
where the first map is obtained by taking the kernel of
![]() $(\tilde{\pi }^{\ast }\varphi -\omega )|_{\tilde{\pi }^{\ast }\mathcal{E}}$
.
$(\tilde{\pi }^{\ast }\varphi -\omega )|_{\tilde{\pi }^{\ast }\mathcal{E}}$
.
This procedure is directly related to the torsion-free pull-back. Recall that
![]() $\chi _{{\rm BNR}}:\overline{\mathcal{T}}\to \mathcal{M}_q$
is the BNR correspondence map and that
$\chi _{{\rm BNR}}:\overline{\mathcal{T}}\to \mathcal{M}_q$
is the BNR correspondence map and that
![]() $p^{\star }_{{\rm tf}}:\overline{{\rm Pic}}(S)\to {\rm Pic}(\widetilde{S})$
is the torsion-free pull-back. Then we have
$p^{\star }_{{\rm tf}}:\overline{{\rm Pic}}(S)\to {\rm Pic}(\widetilde{S})$
is the torsion-free pull-back. Then we have
Proposition 6.3.
![]() $\delta \circ \chi _{{\rm BNR}}=p^{\star }_{{\rm tf}}$
. In particular, if
$\delta \circ \chi _{{\rm BNR}}=p^{\star }_{{\rm tf}}$
. In particular, if
![]() $J\in \overline{\mathcal{T}}_D$
, then
$J\in \overline{\mathcal{T}}_D$
, then
![]() $\delta \circ \chi _{{\rm BNR}}(J)\in \widetilde{\mathcal{T}}_D$
.
$\delta \circ \chi _{{\rm BNR}}(J)\in \widetilde{\mathcal{T}}_D$
.
Proof.
Let
![]() $J\in \overline{\mathcal{T}}$
, and write
$J\in \overline{\mathcal{T}}$
, and write
![]() $(\mathcal{E},\varphi )=\chi _{{\rm BNR}}(J)$
and
$(\mathcal{E},\varphi )=\chi _{{\rm BNR}}(J)$
and
![]() $(\widetilde{\mathcal{E}},\tilde{\varphi }):=\tilde{\pi }^{\ast }(\mathcal{E},\varphi )$
. Recall the BNR exact sequence on
$(\widetilde{\mathcal{E}},\tilde{\varphi }):=\tilde{\pi }^{\ast }(\mathcal{E},\varphi )$
. Recall the BNR exact sequence on
![]() $S$
(see (3)). As
$S$
(see (3)). As
![]() $p^{\ast }$
is right-hand-side exact, we obtain
$p^{\ast }$
is right-hand-side exact, we obtain
Since the spectral curve is
![]() $\widetilde{S}^{\prime}={\rm Im}(\omega )\cup {\rm Im}(-\omega )$
, we can consider the restriction to the component
$\widetilde{S}^{\prime}={\rm Im}(\omega )\cup {\rm Im}(-\omega )$
, we can consider the restriction to the component
![]() ${\rm Im}(\omega )$
and write
${\rm Im}(\omega )$
and write
![]() $\tilde{\lambda }=\omega,\;\widetilde{L}_{\pm }:=\ker (\tilde{\varphi }\mp \omega )$
. We obtain the exact sequence
$\tilde{\lambda }=\omega,\;\widetilde{L}_{\pm }:=\ker (\tilde{\varphi }\mp \omega )$
. We obtain the exact sequence
which breaks into short exact sequences
 \begin{align*} 0\longrightarrow \widetilde{L}_+\longrightarrow \widetilde{\mathcal{E}}\longrightarrow {\rm Im}(\tilde{\varphi }-\omega )\longrightarrow 0\;\\ 0\longrightarrow {\rm Im}(\tilde{\varphi }-\omega )\longrightarrow \widetilde{\mathcal{E}}\otimes \tilde{K}\longrightarrow p^{\ast }J\otimes \tilde{K}\longrightarrow 0. \end{align*}
\begin{align*} 0\longrightarrow \widetilde{L}_+\longrightarrow \widetilde{\mathcal{E}}\longrightarrow {\rm Im}(\tilde{\varphi }-\omega )\longrightarrow 0\;\\ 0\longrightarrow {\rm Im}(\tilde{\varphi }-\omega )\longrightarrow \widetilde{\mathcal{E}}\otimes \tilde{K}\longrightarrow p^{\ast }J\otimes \tilde{K}\longrightarrow 0. \end{align*}
Using the local trivialization in Lemma 6.1,
![]() ${\rm Im}(\tilde{\varphi }-\omega )$
is locally spanned by
${\rm Im}(\tilde{\varphi }-\omega )$
is locally spanned by
![]() $\binom{z^{d_x}}{-z^{m_x}}\mathfrak{e}$
. From Lemma 6.2, if we write
$\binom{z^{d_x}}{-z^{m_x}}\mathfrak{e}$
. From Lemma 6.2, if we write
![]() $\widetilde{L}_0:=\widetilde{L}_+(\Lambda -D)$
and
$\widetilde{L}_0:=\widetilde{L}_+(\Lambda -D)$
and
![]() $\widetilde{L}_1:=\sigma ^{\ast }\widetilde{L}_0$
, then
$\widetilde{L}_1:=\sigma ^{\ast }\widetilde{L}_0$
, then
Moreover, there is an isomorphism
![]() ${\rm Im}(\tilde{\varphi }-\omega )\cong \widetilde{L}_1$
. Letting
${\rm Im}(\tilde{\varphi }-\omega )\cong \widetilde{L}_1$
. Letting
![]() $\widetilde{L}^{\prime}_1$
be the saturation of
$\widetilde{L}^{\prime}_1$
be the saturation of
![]() $\widetilde{L}_1$
, we obtain the commutative diagram:
$\widetilde{L}_1$
, we obtain the commutative diagram:

where
![]() $i:\widetilde{L}_1\to \widetilde{L}^{\prime}_1$
is the natural inclusion. Moreover, in the same trivialization,
$i:\widetilde{L}_1\to \widetilde{L}^{\prime}_1$
is the natural inclusion. Moreover, in the same trivialization,
![]() $\widetilde{L}^{\prime}_1$
is spanned by the section
$\widetilde{L}^{\prime}_1$
is spanned by the section
![]() $\binom{1}{-z^{m_x-d_x}} \mathfrak{e}$
. Therefore,
$\binom{1}{-z^{m_x-d_x}} \mathfrak{e}$
. Therefore,
![]() $\widetilde{L}^{\prime}_1\cong \widetilde{L}_-\otimes \tilde{K}$
, and from Lemma 6.2,
$\widetilde{L}^{\prime}_1\cong \widetilde{L}_-\otimes \tilde{K}$
, and from Lemma 6.2,
![]() $p^{\star }_{{\rm tf}} J=\delta \circ \chi _{{\rm BNR}}(J)$
.
$p^{\star }_{{\rm tf}} J=\delta \circ \chi _{{\rm BNR}}(J)$
.
If
![]() $(\mathcal{E},\varphi )$
is a Higgs bundle with
$(\mathcal{E},\varphi )$
is a Higgs bundle with
![]() $(\mathcal{E},\varphi )=\chi _{{\rm BNR}}(L)$
and
$(\mathcal{E},\varphi )=\chi _{{\rm BNR}}(L)$
and
![]() $\widetilde{L}_0=\delta \circ \chi _{{\rm BNR}}(L)$
, then by Proposition 6.3,
$\widetilde{L}_0=\delta \circ \chi _{{\rm BNR}}(L)$
, then by Proposition 6.3,
![]() $\widetilde{L}_0=p^{\star }_{{\rm tf}}(L)$
. We define a Higgs bundle
$\widetilde{L}_0=p^{\star }_{{\rm tf}}(L)$
. We define a Higgs bundle
![]() $(\widetilde{\mathcal{E}}_0,\tilde{\varphi }_0)$
as follows:
$(\widetilde{\mathcal{E}}_0,\tilde{\varphi }_0)$
as follows:
Moreover,
![]() $\widetilde{\mathcal{E}}$
is an
$\widetilde{\mathcal{E}}$
is an
![]() $\mathcal{O}_{\widetilde{S}}$
submodule of
$\mathcal{O}_{\widetilde{S}}$
submodule of
![]() $\widetilde{\mathcal{E}}_0$
, with a natural inclusion
$\widetilde{\mathcal{E}}_0$
, with a natural inclusion
![]() $\iota :\widetilde{\mathcal{E}}\to \widetilde{\mathcal{E}}_0$
satisfying the following:
$\iota :\widetilde{\mathcal{E}}\to \widetilde{\mathcal{E}}_0$
satisfying the following:
-
(i) the induced morphism
 $\widetilde{\mathcal{E}}\to \widetilde{L}_0,\;\widetilde{\mathcal{E}}\to \sigma ^{\ast }\widetilde{L}_0$
is surjective;
$\widetilde{\mathcal{E}}\to \widetilde{L}_0,\;\widetilde{\mathcal{E}}\to \sigma ^{\ast }\widetilde{L}_0$
is surjective; -
(ii) the restriction of
 $\iota |_{\widetilde{S}\setminus \widetilde{Z}}$
is an isomorphism;
$\iota |_{\widetilde{S}\setminus \widetilde{Z}}$
is an isomorphism; -
(iii)
 $\tilde{\varphi }_0\circ \iota =\iota \circ \tilde{\varphi }$
.
$\tilde{\varphi }_0\circ \iota =\iota \circ \tilde{\varphi }$
.
Following [Reference MochizukiMoc16, Sec. 4.1], we call
![]() $(\widetilde{\mathcal{E}}_0,\tilde{\varphi }_0)$
the abelianization of the Higgs bundle
$(\widetilde{\mathcal{E}}_0,\tilde{\varphi }_0)$
the abelianization of the Higgs bundle
![]() $(\mathcal{E},\varphi )$
.
$(\mathcal{E},\varphi )$
.
6.2 The construction of the algebraic Mochizuki map
In this subsection, we define the algebraic Mochizuki map, as introduced in [Reference MochizukiMoc16]. Recall that for any divisor
![]() $D=\sum _{x\in Z}d_x x$
, there is a canonical weight function
$D=\sum _{x\in Z}d_x x$
, there is a canonical weight function
 \begin{align*}\chi _D(x):=\begin {cases}d_x & x\in \mathrm {supp\;} D\;\\ 0 & x\notin \mathrm {supp\;} D. \end {cases} \end{align*}
\begin{align*}\chi _D(x):=\begin {cases}d_x & x\in \mathrm {supp\;} D\;\\ 0 & x\notin \mathrm {supp\;} D. \end {cases} \end{align*}
We also have the stratification
![]() $\overline{\mathcal{T}}=\cup _D\overline{\mathcal{T}}_D$
for
$\overline{\mathcal{T}}=\cup _D\overline{\mathcal{T}}_D$
for
![]() $\sigma$
divisors
$\sigma$
divisors
![]() $D$
. Let
$D$
. Let
![]() $\mathscr{F}(\widetilde{S})$
be the space of all degree-zero filtered-line bundles over
$\mathscr{F}(\widetilde{S})$
be the space of all degree-zero filtered-line bundles over
![]() $\widetilde{S}$
. The algebraic Mochizuki map
$\widetilde{S}$
. The algebraic Mochizuki map
![]() $\Theta ^{{\rm Moc}}$
is defined as
$\Theta ^{{\rm Moc}}$
is defined as
Example 6.4. When
![]() $q$
has only simple zeros, this construction generalises that of [MSWW16] (see also [Reference FredricksonFre18]). In the case of a quadratic differential with simple zeros, the spectral curve
$q$
has only simple zeros, this construction generalises that of [MSWW16] (see also [Reference FredricksonFre18]). In the case of a quadratic differential with simple zeros, the spectral curve
![]() $S$
is smooth, and every torsion-free sheaf is locally free, so
$S$
is smooth, and every torsion-free sheaf is locally free, so
![]() $\mathcal{T} = \overline{\mathcal{T}}$
. If
$\mathcal{T} = \overline{\mathcal{T}}$
. If
![]() $Z = \{p_1, \dots, p_{4g-4}\}$
are the branch points of
$Z = \{p_1, \dots, p_{4g-4}\}$
are the branch points of
![]() $S$
and if
$S$
and if
![]() $\Lambda = \sum _{i=1}^{4g-4} p_i$
, then the weight function
$\Lambda = \sum _{i=1}^{4g-4} p_i$
, then the weight function
![]() ${1 \over 2}\chi _{-\Lambda }$
assigns a weight of
${1 \over 2}\chi _{-\Lambda }$
assigns a weight of
![]() $-{1 \over 2}$
to each
$-{1 \over 2}$
to each
![]() $p_i$
. For
$p_i$
. For
![]() $L\in \mathcal{T}$
,
$L\in \mathcal{T}$
,
![]() $\Theta ^{{\rm Moc}}(L)=\mathcal{F}_{\ast }(L,\frac 12\chi _{-\Lambda }).$
$\Theta ^{{\rm Moc}}(L)=\mathcal{F}_{\ast }(L,\frac 12\chi _{-\Lambda }).$
Below are some additional properties of
![]() $\Theta ^{{\rm Moc}}$
:
$\Theta ^{{\rm Moc}}$
:
Proposition 6.5.
![]() $\Theta ^{{\rm Moc}}|_{\overline{\mathcal{T}}_D}$
is a continuous map.
$\Theta ^{{\rm Moc}}|_{\overline{\mathcal{T}}_D}$
is a continuous map.
Proof.
This follows directly from the definition of
![]() $\Theta ^{{\rm Moc}}$
and Theorem 3.3.
$\Theta ^{{\rm Moc}}$
and Theorem 3.3.
From Theorem 5.11, we know that for a
![]() $\sigma$
-divisor
$\sigma$
-divisor
![]() $D$
, the preimage of the map
$D$
, the preimage of the map
![]() $p^{\star }_{{\rm tf}}:\overline{\mathcal{T}}_D\to \widetilde{\mathcal{T}}_D$
has dimension
$p^{\star }_{{\rm tf}}:\overline{\mathcal{T}}_D\to \widetilde{\mathcal{T}}_D$
has dimension
![]() $2g-2-{1 \over 2}\deg (D)-r_2/2$
, where
$2g-2-{1 \over 2}\deg (D)-r_2/2$
, where
![]() $r_2$
is the number of odd zeros of
$r_2$
is the number of odd zeros of
![]() $q$
. Even for the top stratum
$q$
. Even for the top stratum
![]() $D=0$
,
$D=0$
,
![]() $p^{\star }_{{\rm tf}}$
is not injective if the spectral curve is not smooth. Indeed, if
$p^{\star }_{{\rm tf}}$
is not injective if the spectral curve is not smooth. Indeed, if
![]() $L_1,L_2\in \overline{\mathcal{T}}_D$
with
$L_1,L_2\in \overline{\mathcal{T}}_D$
with
![]() $p^{\star }_{{\rm tf}}(L_1)=p^{\star }_{{\rm tf}}(L_2)$
, then based on the construction, we have
$p^{\star }_{{\rm tf}}(L_1)=p^{\star }_{{\rm tf}}(L_2)$
, then based on the construction, we have
![]() $\Theta ^{{\rm Moc}}(L_1)=\Theta ^{{\rm Moc}}(L_2)$
. In summary, we have the following result:
$\Theta ^{{\rm Moc}}(L_1)=\Theta ^{{\rm Moc}}(L_2)$
. In summary, we have the following result:
Proposition 6.6.
If
![]() $q\in H^0(K^2)$
is irreducible, then
$q\in H^0(K^2)$
is irreducible, then
![]() $\Theta ^{{\rm Moc}}$
is injective if and only if
$\Theta ^{{\rm Moc}}$
is injective if and only if
![]() $q$
has simple zeros.
$q$
has simple zeros.
6.3 Convergence of subsequences
Fix a locally free
![]() $L_0\in \mathcal{T}$
. Using the isomorphism
$L_0\in \mathcal{T}$
. Using the isomorphism
![]() $\psi _{L_0}:\overline{\mathcal{T}}\to \overline{\mathcal{P}}$
defined by
$\psi _{L_0}:\overline{\mathcal{T}}\to \overline{\mathcal{P}}$
defined by
![]() $\psi _{L_0}(L)=LL_0^{-1}$
, we can extend the Mochizuki map
$\psi _{L_0}(L)=LL_0^{-1}$
, we can extend the Mochizuki map
![]() $\Theta ^{{\rm Moc}}$
to
$\Theta ^{{\rm Moc}}$
to
![]() $\overline{\mathcal{P}}$
. For
$\overline{\mathcal{P}}$
. For
![]() $J\in \overline{\mathcal{P}}_D$
, we write
$J\in \overline{\mathcal{P}}_D$
, we write
![]() $\widetilde{J}:=p^{\star }_{{\rm tf}}(J)$
and choose the weight function
$\widetilde{J}:=p^{\star }_{{\rm tf}}(J)$
and choose the weight function
![]() ${1 \over 2}\chi _D$
. We then define:
${1 \over 2}\chi _D$
. We then define:
Proposition 6.7.
The map
![]() $\Theta ^{{\rm Moc}}_0$
satisfies the following properties:
$\Theta ^{{\rm Moc}}_0$
satisfies the following properties:
-
(i) If
 $J\in \overline{\mathcal{P}}$
and
$J\in \overline{\mathcal{P}}$
and
 $L:=L_0J$
, then
where
$L:=L_0J$
, then
where \begin{align*}\Theta ^{\mathrm {Moc}}_0(J)=\Theta ^{\mathrm {Moc}}(L)\otimes \Theta ^{\mathrm {Moc}}(L_0)^{-1}\,\end{align*}
\begin{align*}\Theta ^{\mathrm {Moc}}_0(J)=\Theta ^{\mathrm {Moc}}(L)\otimes \Theta ^{\mathrm {Moc}}(L_0)^{-1}\,\end{align*}
 $\otimes$
is the tensor product for filtered line bundles
(7)
.
$\otimes$
is the tensor product for filtered line bundles
(7)
.
-
(ii) If
 $L=\tau (I,v)$
, with
$L=\tau (I,v)$
, with
 $(I,v)\in \widehat{{\rm PMod}}(\widetilde{S})$
and with
$(I,v)\in \widehat{{\rm PMod}}(\widetilde{S})$
and with
 $L\in \overline{\mathcal{P}}_D$
, then
where
$L\in \overline{\mathcal{P}}_D$
, then
where \begin{align*} \Theta ^{\mathrm {Moc}}_0\circ \tau (I,v)=\mathcal {F}_{\ast }(I(-D_v), \tfrac {1}{2}\chi _{D_v+\sigma ^{\ast }D_v})\, \end{align*}
\begin{align*} \Theta ^{\mathrm {Moc}}_0\circ \tau (I,v)=\mathcal {F}_{\ast }(I(-D_v), \tfrac {1}{2}\chi _{D_v+\sigma ^{\ast }D_v})\, \end{align*}
 $D_v$
is the corresponding divisor defined in Theorem 5.5
.
$D_v$
is the corresponding divisor defined in Theorem 5.5
.
-
(iii) If
 $\sigma ^{\ast }D_v=D_v$
, then
$\sigma ^{\ast }D_v=D_v$
, then
 $\Theta ^{{\rm Moc}}_0\circ \tau (I,v)=\mathcal{F}_{\ast }(I,0)$
, where
$\Theta ^{{\rm Moc}}_0\circ \tau (I,v)=\mathcal{F}_{\ast }(I,0)$
, where
 $0$
means that all parabolic weights are zero.
$0$
means that all parabolic weights are zero.
Proof.
As
![]() $L_0$
is locally free, we have
$L_0$
is locally free, we have
![]() $p^{\star }_{{\rm tf}} J=(p^{\ast }L_0)^{-1}\otimes p^{\star }_{{\rm tf}} L$
. By definition,
$p^{\star }_{{\rm tf}} J=(p^{\ast }L_0)^{-1}\otimes p^{\star }_{{\rm tf}} L$
. By definition,
which implies (i). For (ii), by Theorem 5.5,
![]() $p^{\star }_{{\rm tf}} L=I(-D_v)$
, and from Proposition 5.12, we have
$p^{\star }_{{\rm tf}} L=I(-D_v)$
, and from Proposition 5.12, we have
![]() $D=D_v+\sigma ^{\ast }D_v$
, which implies (ii). When
$D=D_v+\sigma ^{\ast }D_v$
, which implies (ii). When
![]() $\sigma ^{\ast }D_v=D_v$
, we compute
$\sigma ^{\ast }D_v=D_v$
, we compute
which implies (iii).
We now give a criterion for the continuity of the map
![]() $\Theta ^{{\rm Moc}}$
. By Proposition 6.7, it is sufficient to study the map
$\Theta ^{{\rm Moc}}$
. By Proposition 6.7, it is sufficient to study the map
![]() $\Theta ^{{\rm Moc}}_0$
. Recall that for
$\Theta ^{{\rm Moc}}_0$
. Recall that for
![]() $L\in \overline{\mathcal{P}}$
, we have
$L\in \overline{\mathcal{P}}$
, we have
and that the number
![]() $n_L$
is defined to be the number of divisors
$n_L$
is defined to be the number of divisors
![]() $D_v\in \mathscr{D}_L$
such that
$D_v\in \mathscr{D}_L$
such that
![]() $\sigma ^{\ast }D_v\neq D_v$
.
$\sigma ^{\ast }D_v\neq D_v$
.
Proposition 6.8.
Let
![]() $D$
be a
$D$
be a
![]() $\sigma$
-divisor, with
$\sigma$
-divisor, with
![]() $L\in \overline{\mathcal{P}}_D$
, and assume that
$L\in \overline{\mathcal{P}}_D$
, and assume that
![]() $\Theta ^{{\rm Moc}}_0$
is continuous at
$\Theta ^{{\rm Moc}}_0$
is continuous at
![]() $L$
. Then, for
$L$
. Then, for
![]() $(J,v)\in \mathscr{N}_L$
and
$(J,v)\in \mathscr{N}_L$
and
![]() $D_v\in \mathscr{D}_{L}$
, we have
$D_v\in \mathscr{D}_{L}$
, we have
![]() $\sigma ^{\ast }D_v=D_v$
, i.e.,
$\sigma ^{\ast }D_v=D_v$
, i.e.,
![]() $n_L=0$
.
$n_L=0$
.
Proof.
As the top stratum
![]() $\mathcal{P}$
is dense in
$\mathcal{P}$
is dense in
![]() $\overline{\mathcal{P}}$
, there exists a family
$\overline{\mathcal{P}}$
, there exists a family
![]() $L_i\in \mathcal{P}$
such that
$L_i\in \mathcal{P}$
such that
![]() $\lim _{i\to \infty }L_i=L$
. Let
$\lim _{i\to \infty }L_i=L$
. Let
![]() $(J_i,v_i)\in \widehat{{\rm PMod}}(\widetilde{S})$
be such that
$(J_i,v_i)\in \widehat{{\rm PMod}}(\widetilde{S})$
be such that
![]() $\tau (J_i,v_i)=L_i$
. Then, after passing to subsequences,
$\tau (J_i,v_i)=L_i$
. Then, after passing to subsequences,
![]() $\lim _{i\to \infty }(J_i,v_i)=(J_{\infty },v_{\infty })$
, and
$\lim _{i\to \infty }(J_i,v_i)=(J_{\infty },v_{\infty })$
, and
![]() $\tau (J_{\infty },v_{\infty })=L$
. As
$\tau (J_{\infty },v_{\infty })=L$
. As
![]() $L_i$
is locally free, we have
$L_i$
is locally free, we have
![]() $D_{v_i}=0$
. Moreover, by Theorem 5.5, we have
$D_{v_i}=0$
. Moreover, by Theorem 5.5, we have
![]() $p^{\star }_{{\rm tf}} L=J_{\infty }(-D_{v_\infty })$
, and from Proposition 5.12, we have
$p^{\star }_{{\rm tf}} L=J_{\infty }(-D_{v_\infty })$
, and from Proposition 5.12, we have
![]() $D=D_{v_{\infty }}+\sigma ^{\ast }D_{v_{\infty }}$
. By Proposition 6.3.1, we have
$D=D_{v_{\infty }}+\sigma ^{\ast }D_{v_{\infty }}$
. By Proposition 6.3.1, we have
and we compute
Moreover, by Proposition 6.3.1, we have
Since
![]() $\Theta ^{{\rm Moc}}_0$
is continuous on
$\Theta ^{{\rm Moc}}_0$
is continuous on
![]() $L$
, we have
$L$
, we have
![]() $\lim _{i\to \infty }\Theta ^{{\rm Moc}}_0(L_i)=\Theta ^{{\rm Moc}}(L)$
, which implies that
$\lim _{i\to \infty }\Theta ^{{\rm Moc}}_0(L_i)=\Theta ^{{\rm Moc}}(L)$
, which implies that
![]() $\chi _{D_{v_{\infty }}}=\chi _{\sigma ^{\ast }D_{v_{\infty }}}$
.
$\chi _{D_{v_{\infty }}}=\chi _{\sigma ^{\ast }D_{v_{\infty }}}$
.
By Proposition 5.16,
![]() $n_L\gt 0$
if and only if
$n_L\gt 0$
if and only if
![]() $q$
has at least one zero of even order. Hence, the following is immediate:
$q$
has at least one zero of even order. Hence, the following is immediate:
Corollary 6.9.
Suppose
![]() $q$
is irreducible and has a zero of even order. Then
$q$
is irreducible and has a zero of even order. Then
![]() $\Theta ^{{\rm Moc}}_0$
is not continuous.
$\Theta ^{{\rm Moc}}_0$
is not continuous.
By contrast, we have the following:
Proposition 6.10.
If
![]() $q$
is irreducible with all zeros of odd order, then
$q$
is irreducible with all zeros of odd order, then
![]() $\Theta ^{{\rm Moc}}_0$
is continuous.
$\Theta ^{{\rm Moc}}_0$
is continuous.
Proof.
Since all zeros of
![]() $q$
are odd, for any
$q$
are odd, for any
![]() $L\in \overline{\mathcal{P}}$
we have
$L\in \overline{\mathcal{P}}$
we have
![]() $n_L=0$
. Let
$n_L=0$
. Let
![]() $L_{\infty }\in \overline{\mathcal{P}}$
be fixed, and let
$L_{\infty }\in \overline{\mathcal{P}}$
be fixed, and let
![]() $L_i\in \overline{\mathcal{P}}$
be any sequence such that
$L_i\in \overline{\mathcal{P}}$
be any sequence such that
![]() $\lim _{i\to \infty }L_i=L_{\infty }$
. Since
$\lim _{i\to \infty }L_i=L_{\infty }$
. Since
![]() $\tau :\widehat{{\rm PMod}}(\widetilde{S})\to \overline{\mathcal{P}}$
is bijective, we take
$\tau :\widehat{{\rm PMod}}(\widetilde{S})\to \overline{\mathcal{P}}$
is bijective, we take
![]() $(J_i,v_i)\in \widehat{{\rm PMod}}(\widetilde{S})$
with
$(J_i,v_i)\in \widehat{{\rm PMod}}(\widetilde{S})$
with
![]() $\tau (J_i,v_i)=L_i$
. Moreover, we assume
$\tau (J_i,v_i)=L_i$
. Moreover, we assume
![]() $\lim _{i\to \infty }(J_i,v_i)=(J_{\infty },v_{\infty })$
with
$\lim _{i\to \infty }(J_i,v_i)=(J_{\infty },v_{\infty })$
with
![]() $\tau (J_{\infty },v_{\infty })=L_{\infty }$
. Since
$\tau (J_{\infty },v_{\infty })=L_{\infty }$
. Since
![]() $q$
contains only odd-order zeros, it follows that
$q$
contains only odd-order zeros, it follows that
![]() ${\rm supp\;} D_v\subset {\rm Fix}(\sigma )$
. By Proposition 6.3.1, we have
${\rm supp\;} D_v\subset {\rm Fix}(\sigma )$
. By Proposition 6.3.1, we have
![]() $\Theta ^{{\rm Moc}}_0(L_i)=\mathcal{F}_{\ast }(J_i,0)$
. Therefore, we have:
$\Theta ^{{\rm Moc}}_0(L_i)=\mathcal{F}_{\ast }(J_i,0)$
. Therefore, we have:
This concludes the proof.
Theorem 6.11.
Suppose
![]() $q$
is irreducible. For the map
$q$
is irreducible. For the map
![]() $\Theta ^{{\rm Moc}}:\mathcal{M}_q\rightarrow \mathscr{F}(\widetilde{S})$
, we have:
$\Theta ^{{\rm Moc}}:\mathcal{M}_q\rightarrow \mathscr{F}(\widetilde{S})$
, we have:
-
(i)
 $\Theta ^{{\rm Moc}}$
is injective if and only if
$\Theta ^{{\rm Moc}}$
is injective if and only if
 $q$
has only simple zeros;
$q$
has only simple zeros;
-
(ii) if
 $q$
has only zeros of odd order,
$q$
has only zeros of odd order,
 $\Theta ^{{\rm Moc}}$
is continuous;
$\Theta ^{{\rm Moc}}$
is continuous;
-
(iii) if
 $q$
contains a zero of even order,
$q$
contains a zero of even order,
 $\Theta ^{{\rm Moc}}$
is not continuous.
$\Theta ^{{\rm Moc}}$
is not continuous.
Proof. (i) follows from Proposition 6.6. (ii) follows from Proposition 6.10. (iii) follows from Corollary 6.9.
Proposition 6.12.
Suppose
![]() $n_L\gt 0$
. Then for
$n_L\gt 0$
. Then for
![]() $k=1,\ldots,n_L$
, there exist sequences
$k=1,\ldots,n_L$
, there exist sequences
![]() ${L_i^k}\in \mathcal{P}$
with
${L_i^k}\in \mathcal{P}$
with
![]() $\lim _{i\to \infty }L_i^k=L$
such that if we denote
$\lim _{i\to \infty }L_i^k=L$
such that if we denote
![]() $\mathcal{F}_{\ast }^k:=\lim _{i\to \infty }\Theta ^{{\rm Moc}}_0(L_i^k)$
and
$\mathcal{F}_{\ast }^k:=\lim _{i\to \infty }\Theta ^{{\rm Moc}}_0(L_i^k)$
and
![]() $\mathcal{F}_{\ast }^0:=\Theta ^{{\rm Moc}}_0(L)$
, then
$\mathcal{F}_{\ast }^0:=\Theta ^{{\rm Moc}}_0(L)$
, then
![]() $\mathcal{F}_{\ast }^{k_1}\neq \mathcal{F}_{\ast }^{k_2}$
for
$\mathcal{F}_{\ast }^{k_1}\neq \mathcal{F}_{\ast }^{k_2}$
for
![]() $k_1\neq k_2$
. Moreover, there exist
$k_1\neq k_2$
. Moreover, there exist
![]() $\{D_{1},\ldots,D_{n_L}\}\subset \mathscr{D}_L$
such that
$\{D_{1},\ldots,D_{n_L}\}\subset \mathscr{D}_L$
such that
![]() $\mathcal{F}_{\ast }^{k}=\mathcal{F}_{\ast }(p^{\star }_{{\rm tf}} L,\chi _{D_k})$
.
$\mathcal{F}_{\ast }^{k}=\mathcal{F}_{\ast }(p^{\star }_{{\rm tf}} L,\chi _{D_k})$
.
Proof.
By the definition of
![]() $n_L$
, we can find
$n_L$
, we can find
![]() $(J^k,v^k)$
with
$(J^k,v^k)$
with
![]() $\tau (J^k,v^k)=L$
. If we define
$\tau (J^k,v^k)=L$
. If we define
![]() $D_k:=D_{v^k}$
, then
$D_k:=D_{v^k}$
, then
![]() $\sigma ^{\ast }D_{k}\neq D_{k}$
. Moreover, by Theorem 5.5, we have
$\sigma ^{\ast }D_{k}\neq D_{k}$
. Moreover, by Theorem 5.5, we have
![]() $p^{\star }_{{\rm tf}} L=J^k(-D_k)$
. As
$p^{\star }_{{\rm tf}} L=J^k(-D_k)$
. As
![]() $\tau ^{-1}(\mathcal{P})$
is dense in
$\tau ^{-1}(\mathcal{P})$
is dense in
![]() $\widehat{{\rm PMod}}(\widetilde{S})$
, for each
$\widehat{{\rm PMod}}(\widetilde{S})$
, for each
![]() $(J^k,v^k)$
, we can find a sequence
$(J^k,v^k)$
, we can find a sequence
![]() $(J_{i}^k,v_{i}^k)\in \tau ^{-1}(\mathcal{P})$
such that
$(J_{i}^k,v_{i}^k)\in \tau ^{-1}(\mathcal{P})$
such that
![]() $\lim _{i\to \infty }(J_i^k,v_i^k)=(J^k,v^k)$
, and we define
$\lim _{i\to \infty }(J_i^k,v_i^k)=(J^k,v^k)$
, and we define
![]() $L_i^k:=\tau (J_{i}^k,v_{i}^k)$
. Since
$L_i^k:=\tau (J_{i}^k,v_{i}^k)$
. Since
![]() $L_i^k$
is locally free,
$L_i^k$
is locally free,
![]() $D_{v_i^k}=0$
, and thus
$D_{v_i^k}=0$
, and thus
![]() $\Theta ^{{\rm Moc}}_0(L_i^k)=\mathcal{F}_{\ast }(J_i^k,0)$
. We compute
$\Theta ^{{\rm Moc}}_0(L_i^k)=\mathcal{F}_{\ast }(J_i^k,0)$
. We compute
and
![]() $\Theta ^{{\rm Moc}}_0(L)=\mathcal{F}_{\ast }(p^{\star }_{{\rm tf}} L,\frac 12\chi _{D})$
. Based on our assumptions, we have
$\Theta ^{{\rm Moc}}_0(L)=\mathcal{F}_{\ast }(p^{\star }_{{\rm tf}} L,\frac 12\chi _{D})$
. Based on our assumptions, we have
![]() $D_{k_1}\neq D_{k_2}$
for
$D_{k_1}\neq D_{k_2}$
for
![]() $k_1\neq k_2$
and
$k_1\neq k_2$
and
![]() $\sigma ^{\ast }D_k\neq D_k$
, which implies that
$\sigma ^{\ast }D_k\neq D_k$
, which implies that
![]() $\chi _{D_{k_1}}\neq \chi _{D_{k_2}}$
for
$\chi _{D_{k_1}}\neq \chi _{D_{k_2}}$
for
![]() $k_1\neq k_2$
and
$k_1\neq k_2$
and
![]() $\chi _{D_k}\neq \frac 12\chi _D$
.
$\chi _{D_k}\neq \frac 12\chi _D$
.
We now present a computation for the case of a simple nodal curve:
Example 6.13. Let
![]() $q$
be a quadratic differential with
$q$
be a quadratic differential with
![]() $2g-4$
simple zeros, and let
$2g-4$
simple zeros, and let
![]() $x$
be an even zero of
$x$
be an even zero of
![]() $q$
of order two. Then
$q$
of order two. Then
![]() $S$
has a singular point, which we also denote by
$S$
has a singular point, which we also denote by
![]() $x$
. Let
$x$
. Let
![]() $p:\widetilde{S}\to S$
be the normalisation map and let
$p:\widetilde{S}\to S$
be the normalisation map and let
![]() $p^{-1}(x)=\{x_1,x_2\}$
. Consider the
$p^{-1}(x)=\{x_1,x_2\}$
. Consider the
![]() $\sigma$
-divisor
$\sigma$
-divisor
![]() $D=x_1+x_2$
, and let
$D=x_1+x_2$
, and let
![]() $L\in \overline{\mathcal{P}}_D$
. Then
$L\in \overline{\mathcal{P}}_D$
. Then
![]() $n_L=2$
, and we can write
$n_L=2$
, and we can write
![]() $\mathscr{N}_L={(J_1,v_1),(J_2,v_2)}$
, where
$\mathscr{N}_L={(J_1,v_1),(J_2,v_2)}$
, where
![]() $D_{v_1}=x_1$
and
$D_{v_1}=x_1$
and
![]() $D_{v_2}=x_2$
. Moreover, we have
$D_{v_2}=x_2$
. Moreover, we have
![]() $p^{\star }_{{\rm tf}} L=J_1\otimes \mathcal{O}(-x_1)=J_2\otimes \mathcal{O}(-x_2)$
. Let
$p^{\star }_{{\rm tf}} L=J_1\otimes \mathcal{O}(-x_1)=J_2\otimes \mathcal{O}(-x_2)$
. Let
![]() $(\alpha,\beta )$
denote the parabolic weight that is equal to
$(\alpha,\beta )$
denote the parabolic weight that is equal to
![]() $\alpha$
at
$\alpha$
at
![]() $x_1$
,
$x_1$
,
![]() $\beta$
at
$\beta$
at
![]() $x_2$
, and
$x_2$
, and
![]() $\frac 12$
at all other zeros. Then the filtered bundles obtained in Proposition 6.12 are
$\frac 12$
at all other zeros. Then the filtered bundles obtained in Proposition 6.12 are
6.4 Mochizuki’s convergence theorem for irreducible fibres
In this subsection, we recall Mochizuki’s construction of the limiting configuration metric [Reference MochizukiMoc16, Section 4.2.1, 4.3.2] and the convergence theorem.
6.4.1 Limiting configuration metric
Let
![]() $q$
be an irreducible quadratic differential, and let
$q$
be an irreducible quadratic differential, and let
![]() $(\mathcal{E},\varphi )\in \mathcal{M}_q$
be a Higgs bundle with
$(\mathcal{E},\varphi )\in \mathcal{M}_q$
be a Higgs bundle with
![]() $(\mathcal{E},\varphi )=\chi _{{\rm BNR}}(L)$
. We write
$(\mathcal{E},\varphi )=\chi _{{\rm BNR}}(L)$
. We write
![]() $\widetilde{L}_0=p^{\star }_{{\rm tf}} L$
and
$\widetilde{L}_0=p^{\star }_{{\rm tf}} L$
and
![]() $(\widetilde{\mathcal{E}},\tilde{\varphi }):=p^{\ast }(\mathcal{E},\varphi )$
. Then the abelianization of
$(\widetilde{\mathcal{E}},\tilde{\varphi }):=p^{\ast }(\mathcal{E},\varphi )$
. Then the abelianization of
![]() $(\mathcal{E},\varphi )$
, which is a Higgs bundle over
$(\mathcal{E},\varphi )$
, which is a Higgs bundle over
![]() $\widetilde{S}$
, can be written as
$\widetilde{S}$
, can be written as
![]() $\widetilde{\mathcal{E}}_0=\widetilde{L}_0\oplus \sigma ^{\ast }\widetilde{L}_0,\;\tilde{\varphi }_0={\rm diag}(\omega,\;-\omega )$
. The natural inclusion
$\widetilde{\mathcal{E}}_0=\widetilde{L}_0\oplus \sigma ^{\ast }\widetilde{L}_0,\;\tilde{\varphi }_0={\rm diag}(\omega,\;-\omega )$
. The natural inclusion
![]() $\iota :(\widetilde{\mathcal{E}},\tilde{\varphi })\to (\widetilde{\mathcal{E}}_0,\tilde{\varphi }_0)$
is an isomorphism over
$\iota :(\widetilde{\mathcal{E}},\tilde{\varphi })\to (\widetilde{\mathcal{E}}_0,\tilde{\varphi }_0)$
is an isomorphism over
![]() $\widetilde{S}\setminus \widetilde{Z}$
. Moreover, we let
$\widetilde{S}\setminus \widetilde{Z}$
. Moreover, we let
![]() $D$
be the
$D$
be the
![]() $\sigma$
-divisor of
$\sigma$
-divisor of
![]() $(\mathcal{E},\varphi )$
.
$(\mathcal{E},\varphi )$
.
From the construction of
![]() $\Theta ^{{\rm Moc}}(L)$
and Proposition 6.12, we have
$\Theta ^{{\rm Moc}}(L)$
and Proposition 6.12, we have
![]() $n_L$
different divisors
$n_L$
different divisors
![]() $D_k$
for
$D_k$
for
![]() $k=1,\cdots,n_L$
with
$k=1,\cdots,n_L$
with
![]() $\sigma ^{*}D_k\neq D_k$
and
$\sigma ^{*}D_k\neq D_k$
and
![]() $D_k+\sigma ^{*}D_k=D$
. Moreover, we can find
$D_k+\sigma ^{*}D_k=D$
. Moreover, we can find
![]() $n_L+1$
different filtered bundles with deg
$n_L+1$
different filtered bundles with deg
![]() $0$
. Define
$0$
. Define
which are all degree-zero filtered bundles with different level of filtrations.
Now we will introduce the construction in [Reference MochizukiMoc16, Section 4.2.1, 4.3.2]. For
![]() $k=0,\cdots,n_L$
, we define
$k=0,\cdots,n_L$
, we define
![]() $\tilde{h}_k$
to be the harmonic metric for the filtered bundle
$\tilde{h}_k$
to be the harmonic metric for the filtered bundle
![]() $\mathcal{F}_{*,k}$
; this is well-defined up to a positive multiplicative constant. To fix this constant, assume that
$\mathcal{F}_{*,k}$
; this is well-defined up to a positive multiplicative constant. To fix this constant, assume that
![]() $\sigma ^{\ast }\tilde{h}_k\otimes \tilde{h}_k=1$
. This gives a unique choice of
$\sigma ^{\ast }\tilde{h}_k\otimes \tilde{h}_k=1$
. This gives a unique choice of
![]() $\tilde{h}_k$
. We then define the metric
$\tilde{h}_k$
. We then define the metric
![]() $\widetilde{H}_k={\rm diag}(\tilde{h}_k,\;\sigma ^{\ast }\tilde{h}_k)$
on
$\widetilde{H}_k={\rm diag}(\tilde{h}_k,\;\sigma ^{\ast }\tilde{h}_k)$
on
![]() $\widetilde{\mathcal{E}}_0$
, with
$\widetilde{\mathcal{E}}_0$
, with
![]() $\det (\widetilde{H}_k)=1$
. For the resulting harmonic bundle
$\det (\widetilde{H}_k)=1$
. For the resulting harmonic bundle
![]() $(\widetilde{\mathcal{E}}_0,\varphi _0,\widetilde{H}_k)$
, we define
$(\widetilde{\mathcal{E}}_0,\varphi _0,\widetilde{H}_k)$
, we define
![]() $\tilde{\nabla }_k$
to be the unitary connection determined by
$\tilde{\nabla }_k$
to be the unitary connection determined by
![]() $\widetilde{H}_k$
. Since
$\widetilde{H}_k$
. Since
![]() $\widetilde{H}_k$
is diagonal over
$\widetilde{H}_k$
is diagonal over
![]() $\widetilde{S}\setminus \widetilde{Z}$
, it follows that
$\widetilde{S}\setminus \widetilde{Z}$
, it follows that
![]() $F_{\tilde{\nabla }_k}=0$
, and we have
$F_{\tilde{\nabla }_k}=0$
, and we have
![]() $[\varphi _0,\varphi _0^{\dagger _{\widetilde{H}_k}}]=0$
. Furthermore, as
$[\varphi _0,\varphi _0^{\dagger _{\widetilde{H}_k}}]=0$
. Furthermore, as
![]() $\iota$
is an isomorphism on
$\iota$
is an isomorphism on
![]() $\widetilde{S}\setminus \widetilde{Z}$
, the metric
$\widetilde{S}\setminus \widetilde{Z}$
, the metric
![]() $\widetilde{H}_k$
also defines a metric on
$\widetilde{H}_k$
also defines a metric on
![]() $(\widetilde{\mathcal{E}},\tilde{\varphi })$
over
$(\widetilde{\mathcal{E}},\tilde{\varphi })$
over
![]() $\widetilde{S}\setminus \widetilde{Z}$
.
$\widetilde{S}\setminus \widetilde{Z}$
.
For any
![]() $\tilde{x}\in \widetilde{S}\setminus \widetilde{Z}$
with
$\tilde{x}\in \widetilde{S}\setminus \widetilde{Z}$
with
![]() $x:=p(\tilde{x})$
, we have the isomorphisms
$x:=p(\tilde{x})$
, we have the isomorphisms
Therefore,
![]() $\widetilde{H}_k$
induces a metric
$\widetilde{H}_k$
induces a metric
![]() $H^{{\rm Lim}}_k$
on
$H^{{\rm Lim}}_k$
on
![]() $\Sigma \setminus Z$
, and we may consider
$\Sigma \setminus Z$
, and we may consider
![]() $H^{{\rm Lim}}_k$
as the push-forward of
$H^{{\rm Lim}}_k$
as the push-forward of
![]() $\tilde{h}_k$
. In [Reference HornHor22b, Theorem 5.2], the push-forward metric of
$\tilde{h}_k$
. In [Reference HornHor22b, Theorem 5.2], the push-forward metric of
![]() $\Theta ^{{\rm Moc}}(L)$
is explicitly written in local coordinates.
$\Theta ^{{\rm Moc}}(L)$
is explicitly written in local coordinates.
Recall the notation from Section 2.4. Let
![]() $E$
be a trivial, smooth, rank 2 vector bundle over a Riemann surface
$E$
be a trivial, smooth, rank 2 vector bundle over a Riemann surface
![]() $\Sigma$
, and let
$\Sigma$
, and let
![]() $H_0$
be a background Hermitian metric on
$H_0$
be a background Hermitian metric on
![]() $E$
. Over
$E$
. Over
![]() $\Sigma \setminus Z$
, we write
$\Sigma \setminus Z$
, we write
![]() $\nabla _k^{{\rm Lim}}$
for the Chern connection defined by
$\nabla _k^{{\rm Lim}}$
for the Chern connection defined by
![]() $H_k^{{\rm Lim}}$
, which is unitary with respect to
$H_k^{{\rm Lim}}$
, which is unitary with respect to
![]() $H_0$
, and let
$H_0$
, and let
![]() $\phi ^{{\rm Lim}}_k=\varphi _k^{{\rm Lim}}+\varphi _k^{\dagger _{{\rm Lim}}}$
be the corresponding Higgs field in the unitary gauge. They both satisfy the decoupled Hitchin equations over
$\phi ^{{\rm Lim}}_k=\varphi _k^{{\rm Lim}}+\varphi _k^{\dagger _{{\rm Lim}}}$
be the corresponding Higgs field in the unitary gauge. They both satisfy the decoupled Hitchin equations over
![]() $\Sigma \setminus Z$
. Thus, from any Higgs bundle
$\Sigma \setminus Z$
. Thus, from any Higgs bundle
![]() $(\mathcal{E},\varphi )$
, we obtain
$(\mathcal{E},\varphi )$
, we obtain
![]() $n_L+1$
limiting configurations:
$n_L+1$
limiting configurations:
The flat connection, which is defined over
![]() $\Sigma \setminus Z$
, may be understood by using the nonabelian Hodge correspondence for filtered vector bundles [Reference SimpsonSim90]. Given filtered line bundles
$\Sigma \setminus Z$
, may be understood by using the nonabelian Hodge correspondence for filtered vector bundles [Reference SimpsonSim90]. Given filtered line bundles
![]() $\mathcal{F}_{*,k}$
, define filtered vector bundles
$\mathcal{F}_{*,k}$
, define filtered vector bundles
![]() $\widetilde{\mathcal{E}}_{*,k}:=\mathcal{F}_{*,k}\oplus \sigma ^{*}\mathcal{F}_{*,k}$
, which can be explicitly written as
$\widetilde{\mathcal{E}}_{*,k}:=\mathcal{F}_{*,k}\oplus \sigma ^{*}\mathcal{F}_{*,k}$
, which can be explicitly written as
 \begin{align} \widetilde{\mathcal{E}}_{*,0} & :=\mathcal{F}_{*}(\widetilde{L}_0,\chi _{\frac 12(D-\Lambda )})\oplus \mathcal{F}_{*}(\sigma ^{*}\widetilde{L}_0,\chi _{\frac 12(D-\Lambda )})\ ;\nonumber\\[4pt] \widetilde{\mathcal{E}}_{*,k} & :=\mathcal{F}_{*}(\widetilde{L}_0,\chi _{D_k-\frac 12\Lambda })\oplus \mathcal{F}_{*}(\sigma ^{*}\widetilde{L}_0,\chi _{\sigma ^{*}D_k-\frac 12\Lambda })\, \ k\neq 0. \end{align}
\begin{align} \widetilde{\mathcal{E}}_{*,0} & :=\mathcal{F}_{*}(\widetilde{L}_0,\chi _{\frac 12(D-\Lambda )})\oplus \mathcal{F}_{*}(\sigma ^{*}\widetilde{L}_0,\chi _{\frac 12(D-\Lambda )})\ ;\nonumber\\[4pt] \widetilde{\mathcal{E}}_{*,k} & :=\mathcal{F}_{*}(\widetilde{L}_0,\chi _{D_k-\frac 12\Lambda })\oplus \mathcal{F}_{*}(\sigma ^{*}\widetilde{L}_0,\chi _{\sigma ^{*}D_k-\frac 12\Lambda })\, \ k\neq 0. \end{align}
These are polystable filtered vector bundles over
![]() $\widetilde{S}\setminus \widetilde{Z}$
. As for each
$\widetilde{S}\setminus \widetilde{Z}$
. As for each
![]() $k=0,\cdots,n_L$
,
$k=0,\cdots,n_L$
,
![]() $\sigma ^{*}\widetilde{\mathcal{E}}_{*,k}=\widetilde{\mathcal{E}}_{*,k}$
, the filtered bundles
$\sigma ^{*}\widetilde{\mathcal{E}}_{*,k}=\widetilde{\mathcal{E}}_{*,k}$
, the filtered bundles
![]() $\widetilde{\mathcal{E}}_{*,k}$
induce filtered vector bundles
$\widetilde{\mathcal{E}}_{*,k}$
induce filtered vector bundles
![]() $\mathcal{E}_{*,k}$
over
$\mathcal{E}_{*,k}$
over
![]() $\Sigma \setminus Z$
. The flat connections
$\Sigma \setminus Z$
. The flat connections
![]() $\nabla _k^{{\rm Lim}}$
will be the unique harmonic unitary connections corresponding to the
$\nabla _k^{{\rm Lim}}$
will be the unique harmonic unitary connections corresponding to the
![]() $\mathcal{E}_{*,k}$
. Moreover, for
$\mathcal{E}_{*,k}$
. Moreover, for
![]() $0\leq k_1\neq k_2\leq n_L$
, based on the definition of
$0\leq k_1\neq k_2\leq n_L$
, based on the definition of
![]() $D_{k_1}$
and
$D_{k_1}$
and
![]() $D_{k_2}$
, we can always find
$D_{k_2}$
, we can always find
![]() $\tilde{x}\in \widetilde{Z}_{{\rm even}}$
, a preimage of an even zero
$\tilde{x}\in \widetilde{Z}_{{\rm even}}$
, a preimage of an even zero
![]() $x$
of
$x$
of
![]() $q$
, such that
$q$
, such that
![]() $\widetilde{\mathcal{E}}_{*,k_1}$
and
$\widetilde{\mathcal{E}}_{*,k_1}$
and
![]() $\widetilde{\mathcal{E}}_{*,k_2}$
have different filtered structures near
$\widetilde{\mathcal{E}}_{*,k_2}$
have different filtered structures near
![]() $\tilde{x}$
. Since
$\tilde{x}$
. Since
![]() $\widetilde{S}\to \Sigma$
is not a branched covering over even zeros,
$\widetilde{S}\to \Sigma$
is not a branched covering over even zeros,
![]() $\widetilde{S}\to \Sigma$
we conclude that near
$\widetilde{S}\to \Sigma$
we conclude that near
![]() $x$
,
$x$
,
![]() $\mathcal{E}_{*,k_1}$
and
$\mathcal{E}_{*,k_1}$
and
![]() $\mathcal{E}_{*,k_2}$
are different filtered bundles. By [Reference SimpsonSim90, Main theorem], the harmonic connections
$\mathcal{E}_{*,k_2}$
are different filtered bundles. By [Reference SimpsonSim90, Main theorem], the harmonic connections
![]() $\nabla _{k_1}$
and
$\nabla _{k_1}$
and
![]() $\nabla _{k_2}$
are not gauge equivalent.
$\nabla _{k_2}$
are not gauge equivalent.
We therefore conclude the following:
Proposition 6.14.
For
![]() $0\leq k_1\neq k_2\leq n_L$
,
$0\leq k_1\neq k_2\leq n_L$
,
![]() $(\nabla _{k_1}^{{\rm Lim}},\phi _{k_1}^{{\rm Lim}})$
and
$(\nabla _{k_1}^{{\rm Lim}},\phi _{k_1}^{{\rm Lim}})$
and
![]() $(\nabla _{k_2}^{{\rm Lim}},\phi _{k_2}^{{\rm Lim}})$
are not gauge equivalent in
$(\nabla _{k_2}^{{\rm Lim}},\phi _{k_2}^{{\rm Lim}})$
are not gauge equivalent in
![]() $\mathcal{M}_{{\rm Hit}}^{{\rm Lim}}$
.
$\mathcal{M}_{{\rm Hit}}^{{\rm Lim}}$
.
Moreover, as with the algebraic compactification of the elements in the
![]() $\mathbb{C}^{\ast }$
orbit, we would like to compare with the limiting configurations in the space
$\mathbb{C}^{\ast }$
orbit, we would like to compare with the limiting configurations in the space
![]() $\mathcal{M}_{{\rm Hit}}^{{\rm Lim}}/\mathbb{C}^{\ast }$
. Over the Dolbeault moduli space
$\mathcal{M}_{{\rm Hit}}^{{\rm Lim}}/\mathbb{C}^{\ast }$
. Over the Dolbeault moduli space
![]() $\mathcal{M}_{{\rm Dol}}$
, there is a natural
$\mathcal{M}_{{\rm Dol}}$
, there is a natural
![]() $\mathbb{Z}_2$
action given by
$\mathbb{Z}_2$
action given by
![]() $(\mathcal{E},\varphi )\to (\mathcal{E},-\varphi )$
, and the fixed point of the
$(\mathcal{E},\varphi )\to (\mathcal{E},-\varphi )$
, and the fixed point of the
![]() $\mathbb{Z}_2$
action is defined to be the real locus of the Dolbeault moduli space, which we denoted by
$\mathbb{Z}_2$
action is defined to be the real locus of the Dolbeault moduli space, which we denoted by
![]() $\mathcal{M}_{{\rm Dol}}^{\mathbb{R}}$
. It follows from [Reference HauselHau98, Theorem 6.2] that the source of the orbifold points of the algebraic compactification comes from the quotient of the real locus. Moreover, for
$\mathcal{M}_{{\rm Dol}}^{\mathbb{R}}$
. It follows from [Reference HauselHau98, Theorem 6.2] that the source of the orbifold points of the algebraic compactification comes from the quotient of the real locus. Moreover, for
![]() $(\mathcal{E},\varphi )=\chi _{{\rm BNR}}(L)$
,
$(\mathcal{E},\varphi )=\chi _{{\rm BNR}}(L)$
,
![]() $(\mathcal{E},\varphi )\in \mathcal{M}_{{\rm Dol}}^{\mathbb{R}}$
if and only if
$(\mathcal{E},\varphi )\in \mathcal{M}_{{\rm Dol}}^{\mathbb{R}}$
if and only if
![]() $\sigma ^{*}L=L$
.
$\sigma ^{*}L=L$
.
Given a Higgs bundle
![]() $(\mathcal{E},\varphi )$
, under the previous convention we let
$(\mathcal{E},\varphi )$
, under the previous convention we let
be the abelianization of
![]() $(\mathcal{E},\varphi )$
. Note that
$(\mathcal{E},\varphi )$
. Note that
![]() $\sigma ^{*}(\widetilde{\mathcal{E}}_0,\tilde{\varphi }_0)=(\widetilde{\mathcal{E}}_0,\tilde{\varphi }_0)$
and that
$\sigma ^{*}(\widetilde{\mathcal{E}}_0,\tilde{\varphi }_0)=(\widetilde{\mathcal{E}}_0,\tilde{\varphi }_0)$
and that
![]() $\widetilde{L}_0$
is the eigenline bundle for
$\widetilde{L}_0$
is the eigenline bundle for
![]() $\tilde{\varphi }_0$
with eigenvalue
$\tilde{\varphi }_0$
with eigenvalue
![]() $\omega$
. Therefore,
$\omega$
. Therefore,
![]() $(\widetilde{\mathcal{E}}_0,\tilde{\varphi }_0)$
is gauge equivalent to
$(\widetilde{\mathcal{E}}_0,\tilde{\varphi }_0)$
is gauge equivalent to
![]() $(\widetilde{\mathcal{E}}_0,-\tilde{\varphi }_0)$
if and only if
$(\widetilde{\mathcal{E}}_0,-\tilde{\varphi }_0)$
if and only if
![]() $\widetilde{L}_0=\sigma ^{*}\widetilde{L}_0$
, which is equivalent to saying that
$\widetilde{L}_0=\sigma ^{*}\widetilde{L}_0$
, which is equivalent to saying that
![]() $(\mathcal{E},\varphi )$
lies in the real locus. For the collection of divisors
$(\mathcal{E},\varphi )$
lies in the real locus. For the collection of divisors
![]() $\mathscr{D}:=\{D_1,\cdots,D_{n_L}\}$
, for any
$\mathscr{D}:=\{D_1,\cdots,D_{n_L}\}$
, for any
![]() $D_k\in \mathscr{D}$
, we have
$D_k\in \mathscr{D}$
, we have
![]() $\sigma ^*D_k\in \mathscr{D}$
. Therefore, there exists a permutation of the index
$\sigma ^*D_k\in \mathscr{D}$
. Therefore, there exists a permutation of the index
![]() $\tau :\{1,\cdots, n_L\}\to \{1,\cdots,n_L\}$
such that
$\tau :\{1,\cdots, n_L\}\to \{1,\cdots,n_L\}$
such that
![]() $D_{\tau (k)}=\sigma ^{*}D_k$
with
$D_{\tau (k)}=\sigma ^{*}D_k$
with
![]() $\tau^2={\rm id}$
.
$\tau^2={\rm id}$
.
Suppose that for the limiting configurations in (23),
![]() $(\widetilde{\mathcal{E}}_{*,k_1},\varphi _0)$
is gauge equivalent to
$(\widetilde{\mathcal{E}}_{*,k_1},\varphi _0)$
is gauge equivalent to
![]() $(\widetilde{\mathcal{E}}_{*,k_2},-\varphi _0)$
. Then the eigenline bundle for eigenvalue
$(\widetilde{\mathcal{E}}_{*,k_2},-\varphi _0)$
. Then the eigenline bundle for eigenvalue
![]() $\omega$
will be gauge equivalent, which implies
$\omega$
will be gauge equivalent, which implies
The above equality holds if and only if
![]() $\widetilde{L}_0=\sigma ^{*}\widetilde{L}_0$
and
$\widetilde{L}_0=\sigma ^{*}\widetilde{L}_0$
and
![]() $k_1=\tau (k_2)$
. In summary, we conclude the following:
$k_1=\tau (k_2)$
. In summary, we conclude the following:
Proposition 6.15.
Let
![]() $[(\nabla _k^{{\rm Lim}},\phi _{k}^{{\rm Lim}})]$
be the
$[(\nabla _k^{{\rm Lim}},\phi _{k}^{{\rm Lim}})]$
be the
![]() $\mathbb{C}^{\ast }$
equivalence class of
$\mathbb{C}^{\ast }$
equivalence class of
![]() $(\nabla _k^{{\rm Lim}},\phi _{k}^{{\rm Lim}})$
in the space
$(\nabla _k^{{\rm Lim}},\phi _{k}^{{\rm Lim}})$
in the space
![]() $\mathcal{M}_{{\rm Hit}}^{{\rm Lim}}/\mathbb{C}^{\ast }$
. Then the following hold:
$\mathcal{M}_{{\rm Hit}}^{{\rm Lim}}/\mathbb{C}^{\ast }$
. Then the following hold:
-
(i) If
 $(\mathcal{E},\varphi )\notin \mathcal{M}_{{\rm Dol}}^{\mathbb{R}}$
, then for any
$(\mathcal{E},\varphi )\notin \mathcal{M}_{{\rm Dol}}^{\mathbb{R}}$
, then for any
 $0\leq k_1\neq k_2\leq n_L$
,
$0\leq k_1\neq k_2\leq n_L$
,
 $[(\nabla _{k_1}^{{\rm Lim}},\phi _{k_1}^{{\rm Lim}})]\neq [(\nabla _{k_2}^{{\rm Lim}},\phi _{k_2}^{{\rm Lim}})]$
in
$[(\nabla _{k_1}^{{\rm Lim}},\phi _{k_1}^{{\rm Lim}})]\neq [(\nabla _{k_2}^{{\rm Lim}},\phi _{k_2}^{{\rm Lim}})]$
in
 $\mathcal{M}_{{\rm Hit}}^{{\rm Lim}}/\mathbb{C}^{\ast }$
.
$\mathcal{M}_{{\rm Hit}}^{{\rm Lim}}/\mathbb{C}^{\ast }$
. -
(ii) If
 $(\mathcal{E},\varphi )\in \mathcal{M}_{{\rm Dol}}^{\mathbb{R}}$
, then
$(\mathcal{E},\varphi )\in \mathcal{M}_{{\rm Dol}}^{\mathbb{R}}$
, then
 $[(\nabla _{k_1}^{{\rm Lim}},\phi _{k_1}^{{\rm Lim}})]=[(\nabla _{k_2}^{{\rm Lim}},\phi _{k_2}^{{\rm Lim}})]$
in
$[(\nabla _{k_1}^{{\rm Lim}},\phi _{k_1}^{{\rm Lim}})]=[(\nabla _{k_2}^{{\rm Lim}},\phi _{k_2}^{{\rm Lim}})]$
in
 $\mathcal{M}_{{\rm Hit}}^{{\rm Lim}}/\mathbb{C}^{\ast }$
if and only if
$\mathcal{M}_{{\rm Hit}}^{{\rm Lim}}/\mathbb{C}^{\ast }$
if and only if
 $k_1=k_2$
or
$k_1=k_2$
or
 $k_1=\tau (k_2)$
.
$k_1=\tau (k_2)$
.
In particular, when
![]() $(\mathcal{E},\varphi )\notin \mathcal{M}_{{\rm Dol}}^{\mathbb{R}}$
, we obtain
$(\mathcal{E},\varphi )\notin \mathcal{M}_{{\rm Dol}}^{\mathbb{R}}$
, we obtain
![]() $1+2n_D$
different
$1+2n_D$
different
![]() $\mathbb{C}^{\ast }$
equivalence classes of the limiting configurations in
$\mathbb{C}^{\ast }$
equivalence classes of the limiting configurations in
![]() $\mathcal{M}_{{\rm Hit}}^{{\rm Lim}}/\mathbb{C}^{\ast }$
, and when
$\mathcal{M}_{{\rm Hit}}^{{\rm Lim}}/\mathbb{C}^{\ast }$
, and when
![]() $(\mathcal{E},\varphi )\in \mathcal{M}_{{\rm Dol}}^{\mathbb{R}}$
, we obtain
$(\mathcal{E},\varphi )\in \mathcal{M}_{{\rm Dol}}^{\mathbb{R}}$
, we obtain
![]() $1+n_D$
different
$1+n_D$
different
![]() $\mathbb{C}^{\ast }$
equivalence classes of limiting configurations in
$\mathbb{C}^{\ast }$
equivalence classes of limiting configurations in
![]() $\mathcal{M}_{{\rm Hit}}^{{\rm Lim}}/\mathbb{C}^{\ast }$
.
$\mathcal{M}_{{\rm Hit}}^{{\rm Lim}}/\mathbb{C}^{\ast }$
.
We define the analytic Mochizuki map
![]() $\Upsilon ^{{\rm Moc}}$
as
$\Upsilon ^{{\rm Moc}}$
as
which we recall is the limiting configuration defined by
![]() $\Theta ^{{\rm Moc}}(L)$
.
$\Theta ^{{\rm Moc}}(L)$
.
6.4.2 The continuity of the limiting configurations
We now introduce the main result of Mochizuki [Reference MochizukiMoc16]. Fix
![]() $(\mathcal{E},\varphi )=\chi _{{\rm BNR}}(L)\in \mathcal{M}_q$
. For any real parameter
$(\mathcal{E},\varphi )=\chi _{{\rm BNR}}(L)\in \mathcal{M}_q$
. For any real parameter
![]() $t\gt 0$
,
$t\gt 0$
,
![]() $(\mathcal{E},t\varphi )$
is a stable Higgs bundle. By the Kobayashi–Hitchin correspondence, there exists a unique metric
$(\mathcal{E},t\varphi )$
is a stable Higgs bundle. By the Kobayashi–Hitchin correspondence, there exists a unique metric
![]() $H_t$
that solves the Hitchin equation. Denote by
$H_t$
that solves the Hitchin equation. Denote by
![]() $\nabla _t$
the unitary connection defined by
$\nabla _t$
the unitary connection defined by
![]() $H_t$
, and write
$H_t$
, and write
![]() $\mathcal{D}_t=\nabla _t+t\phi _t$
for the full
$\mathcal{D}_t=\nabla _t+t\phi _t$
for the full
![]() ${\rm SL}(2,\mathbb{C})$
flat connection. We then have:
${\rm SL}(2,\mathbb{C})$
flat connection. We then have:
Theorem 6.16.
The family
![]() $(\mathcal{E},t\varphi )$
has a unique limiting configuration
$(\mathcal{E},t\varphi )$
has a unique limiting configuration
![]() $\Upsilon ^{{\rm Moc}}(\mathcal{E},\varphi )$
such that for any compact set
$\Upsilon ^{{\rm Moc}}(\mathcal{E},\varphi )$
such that for any compact set
![]() $K\subset \Sigma \setminus Z$
,
$K\subset \Sigma \setminus Z$
,
Moreover, if write
![]() $(\mathcal{E},\varphi )=\chi _{{\rm BNR}}(L)$
and suppose that
$(\mathcal{E},\varphi )=\chi _{{\rm BNR}}(L)$
and suppose that
![]() $L=p_*\widetilde{L}$
, then there exist
$L=p_*\widetilde{L}$
, then there exist
![]() $t$
-independent positive constants
$t$
-independent positive constants
![]() $C_{l,K}$
and
$C_{l,K}$
and
![]() $C^{\prime}_{l,K}$
such that
$C^{\prime}_{l,K}$
such that
Because the map
![]() $\Upsilon ^{{\rm Moc}}$
is the composition of
$\Upsilon ^{{\rm Moc}}$
is the composition of
![]() $\Theta ^{{\rm Moc}} \circ \chi _{{\rm BNR}}^{-1}$
with the nonabelian Hodge correspondence, the behavior of
$\Theta ^{{\rm Moc}} \circ \chi _{{\rm BNR}}^{-1}$
with the nonabelian Hodge correspondence, the behavior of
![]() $\Upsilon ^{{\rm Moc}}$
is the same as
$\Upsilon ^{{\rm Moc}}$
is the same as
![]() $\Theta ^{{\rm Moc}}$
. Recall the decomposition
$\Theta ^{{\rm Moc}}$
. Recall the decomposition
![]() $\mathcal{M}_q = \bigcup \mathcal{M}_{q,D}$
from the end of Section 5. By Theorem 6.11, Proposition 6.12, Proposition 6.14 and Proposition 6.15, we obtain:
$\mathcal{M}_q = \bigcup \mathcal{M}_{q,D}$
from the end of Section 5. By Theorem 6.11, Proposition 6.12, Proposition 6.14 and Proposition 6.15, we obtain:
Theorem 6.17.
Let
![]() $q$
be an irreducible quadratic differential. The map
$q$
be an irreducible quadratic differential. The map
![]() $\Upsilon ^{{\rm Moc}}: \mathcal{M}_q \to \mathcal{M}_{{\rm Hit}}^{{\rm Lim}}$
satisfies the following properties:
$\Upsilon ^{{\rm Moc}}: \mathcal{M}_q \to \mathcal{M}_{{\rm Hit}}^{{\rm Lim}}$
satisfies the following properties:
-
(i) if all the zeros of
 $q$
are odd, then
$q$
are odd, then
 $\Upsilon ^{{\rm Moc}}$
is continuous;
$\Upsilon ^{{\rm Moc}}$
is continuous;
-
(ii) if at least one zero of
 $q$
is even, then for each
$q$
is even, then for each
 $(\mathcal{F}, \psi ) \in \mathcal{M}_{q,D}$
, there exists an integer
$(\mathcal{F}, \psi ) \in \mathcal{M}_{q,D}$
, there exists an integer
 $2n_D$
that depends only on
$2n_D$
that depends only on
 $D$
and
$D$
and
 $2n_D$
sequences
$2n_D$
sequences
 $\{(\mathcal{E}_i^k, \varphi _i^k)\}$
for
$\{(\mathcal{E}_i^k, \varphi _i^k)\}$
for
 $k=1, \dots, 2n_D$
, such that
$k=1, \dots, 2n_D$
, such that
-
*
 $\lim _{i\to \infty }(\mathcal{E}_i^k,\varphi _i^k)=(\mathcal{F},\psi )$
for
$\lim _{i\to \infty }(\mathcal{E}_i^k,\varphi _i^k)=(\mathcal{F},\psi )$
for
 $k=1,\ldots,2n_D$
;
$k=1,\ldots,2n_D$
; -
* and if we write
 \begin{align*}\eta ^k:=\lim _{i\to \infty }\Upsilon ^{\mathrm {Moc}}(\mathcal {E}_i^k,t_i\varphi _i^k)\quad,\quad \xi :=\lim _{i\to \infty }\Upsilon ^{\mathrm {Moc}}(\mathcal {F},t_i\psi )\;\end{align*}
\begin{align*}\eta ^k:=\lim _{i\to \infty }\Upsilon ^{\mathrm {Moc}}(\mathcal {E}_i^k,t_i\varphi _i^k)\quad,\quad \xi :=\lim _{i\to \infty }\Upsilon ^{\mathrm {Moc}}(\mathcal {F},t_i\psi )\;\end{align*}
-
• if
 $(\mathcal{F},\psi )$
doesn’t lie in the real locus, then
$(\mathcal{F},\psi )$
doesn’t lie in the real locus, then
 $\xi,\eta^1,\ldots,\eta ^{2n_D}$
are
$\xi,\eta^1,\ldots,\eta ^{2n_D}$
are
 $2n_D+1$
different limiting configurations;
$2n_D+1$
different limiting configurations;
-
• if
 $(\mathcal{F},\psi )$
lies in the real locus, then
$(\mathcal{F},\psi )$
lies in the real locus, then
 $\eta ^i\cong \eta ^{n_D+i}$
for
$\eta ^i\cong \eta ^{n_D+i}$
for
 $i=1,\cdots,n$
, and we obtain
$i=1,\cdots,n$
, and we obtain
 $n_D+1$
different limiting configurations.
$n_D+1$
different limiting configurations.
-
7. Reducible singular fibre and the Mochizuki map
We now investigate properties of the Hitchin fibre associated with a reducible quadratic differential, as discussed in [Reference Gothen and OliveiraGO13]. Additionally, we provide an overview of Mochizuki’s technique for constructing limiting configurations of Hitchin fibres for reducible quadratic differentials, as detailed in [Reference MochizukiMoc16]. We also analyse the continuity of the Mochizuki map.
7.1 Local description of a Higgs bundle
Write
![]() $q=-\omega \otimes \omega$
with
$q=-\omega \otimes \omega$
with
![]() $\omega \in H^0(K)$
,
$\omega \in H^0(K)$
,
![]() $\Lambda ={\rm Div}(\omega )$
,
$\Lambda ={\rm Div}(\omega )$
,
![]() $Z={\rm supp\;}(\Lambda )$
and
$Z={\rm supp\;}(\Lambda )$
and
![]() $\mathcal{M}_q=\mathcal{H}^{-1}(q)$
. Compared to the irreducible case,
$\mathcal{M}_q=\mathcal{H}^{-1}(q)$
. Compared to the irreducible case,
![]() $\mathcal{M}_q$
contains strictly semistable Higgs bundles, so we let
$\mathcal{M}_q$
contains strictly semistable Higgs bundles, so we let
![]() $\mathcal{M}_q^{\textrm{st}}$
denote the stable locus. We point out that there is a sign ambiguity in the choice of
$\mathcal{M}_q^{\textrm{st}}$
denote the stable locus. We point out that there is a sign ambiguity in the choice of
![]() $\omega$
, which actually plays an important role in the following:
$\omega$
, which actually plays an important role in the following:
7.1.1 Local description
Given a Higgs bundle
![]() $(\mathcal{E},\varphi )$
with
$(\mathcal{E},\varphi )$
with
![]() $\det (\varphi )=q$
, define the line bundles
$\det (\varphi )=q$
, define the line bundles
Then the inclusion maps
![]() $L_{\pm }\to \mathcal{E}$
are injective. Similarly, we may define an abelianisation of
$L_{\pm }\to \mathcal{E}$
are injective. Similarly, we may define an abelianisation of
![]() $(\mathcal{E},\varphi )$
by
$(\mathcal{E},\varphi )$
by
![]() $(\mathcal{E}_0=L_+\oplus L_-,\varphi _0={\rm diag}(\omega,-\omega ))$
. We then have the natural inclusion
$(\mathcal{E}_0=L_+\oplus L_-,\varphi _0={\rm diag}(\omega,-\omega ))$
. We then have the natural inclusion
![]() $\iota :\mathcal{E}_0\to \mathcal{E}$
, which is an isomorphism on
$\iota :\mathcal{E}_0\to \mathcal{E}$
, which is an isomorphism on
![]() $\Sigma \setminus Z$
, and
$\Sigma \setminus Z$
, and
![]() $\varphi \circ \iota =\iota \circ \varphi _0$
.
$\varphi \circ \iota =\iota \circ \varphi _0$
.
It follows from [Reference Gothen and OliveiraGO13, Prop. 7.10] that
![]() $L_{\pm }$
are the only
$L_{\pm }$
are the only
![]() $\varphi$
-invariant subbundles of
$\varphi$
-invariant subbundles of
![]() $\mathcal{E}$
. If we write
$\mathcal{E}$
. If we write
![]() $d_{\pm }:=\deg (L_{\pm })$
, then
$d_{\pm }:=\deg (L_{\pm })$
, then
![]() $(\mathcal{E},\varphi )$
is stable (resp. semistable) if and only if
$(\mathcal{E},\varphi )$
is stable (resp. semistable) if and only if
![]() $d_{\pm }\lt 0\ ({\rm resp.}\ \leq 0)$
. As
$d_{\pm }\lt 0\ ({\rm resp.}\ \leq 0)$
. As
![]() $\det (\mathcal{E})=\mathcal{O}$
, the map
$\det (\mathcal{E})=\mathcal{O}$
, the map
![]() $\det (\iota ):L_+\otimes L_-\to \mathcal{O}$
defines a divisor
$\det (\iota ):L_+\otimes L_-\to \mathcal{O}$
defines a divisor
![]() $D={\rm Div}(\det (\iota ))$
such that
$D={\rm Div}(\det (\iota ))$
such that
![]() $L_+\otimes L_-=\mathcal{O}(-D).$
Therefore, we obtain
$L_+\otimes L_-=\mathcal{O}(-D).$
Therefore, we obtain
and
![]() $0\leq D\leq \Lambda$
. The Higgs bundle
$0\leq D\leq \Lambda$
. The Higgs bundle
![]() $(\mathcal{E},\varphi )$
is semistable if and only if
$(\mathcal{E},\varphi )$
is semistable if and only if
![]() $-\deg D\leq d_+\leq 0$
and is stable if the equalities are strict. For the rest of this section, we will always write
$-\deg D\leq d_+\leq 0$
and is stable if the equalities are strict. For the rest of this section, we will always write
![]() $D=\sum _{p\in Z}\ell _p p$
.
$D=\sum _{p\in Z}\ell _p p$
.
By
![]() $\mathcal{M}_{q,D}$
we mean the set of Higgs bundles
$\mathcal{M}_{q,D}$
we mean the set of Higgs bundles
![]() $(\mathcal{E},\varphi )\in \mathcal{M}_q$
for which the relation
$(\mathcal{E},\varphi )\in \mathcal{M}_q$
for which the relation
![]() $L_+\otimes L_- = \mathcal{O}(-D)$
holds. Consequently, we have
$L_+\otimes L_- = \mathcal{O}(-D)$
holds. Consequently, we have
![]() $ \mathcal{M}_q=\bigcup _{0\leq D\leq \Lambda }\mathcal{M}_{q,D}$
.
$ \mathcal{M}_q=\bigcup _{0\leq D\leq \Lambda }\mathcal{M}_{q,D}$
.
7.1.2 Semistable settings
As the fibre
![]() $\mathcal{M}_q$
might contain strictly semistable Higgs bundles, we now explicitly enumerate all of the possible
$\mathcal{M}_q$
might contain strictly semistable Higgs bundles, we now explicitly enumerate all of the possible
![]() $S$
-equivalence classes. When
$S$
-equivalence classes. When
![]() $D=0$
, then
$D=0$
, then
![]() $L_-=L_+^{-1}$
and
$L_-=L_+^{-1}$
and
![]() $\deg (L_+)=0$
. The corresponding Higgs bundle is polystable and can be explicitly written as
$\deg (L_+)=0$
. The corresponding Higgs bundle is polystable and can be explicitly written as
where
![]() $L\in {\rm Jac}(\Sigma )$
. When
$L\in {\rm Jac}(\Sigma )$
. When
![]() $D\neq 0$
, suppose
$D\neq 0$
, suppose
![]() $\deg (L_+)=-\deg (D)$
. Then
$\deg (L_+)=-\deg (D)$
. Then
![]() $L_-=L_+^{-1}(-D)$
and
$L_-=L_+^{-1}(-D)$
and
![]() $\deg (L_-)=0$
. Under
$\deg (L_-)=0$
. Under
![]() $S$
-equivalence, the polystable Higgs bundle is
$S$
-equivalence, the polystable Higgs bundle is
where
![]() $L_+\in {\rm Pic}^{-\deg (D)}(\Sigma )$
.
$L_+\in {\rm Pic}^{-\deg (D)}(\Sigma )$
.
7.2 Reducible spectral curves
In this subsection, we introduce the algebraic data in [Reference Gothen and OliveiraGO13], which describes the singular fibre with a reducible spectral curve. This plays a similar role to the parabolic modules. See [Reference Gothen and OliveiraGO13, Sec. 7.1] for more details.
For any effective divisor
![]() $D$
and line bundle
$D$
and line bundle
![]() $L$
, define the space
$L$
, define the space
where
![]() $s_1\sim s_2$
if and only if
$s_1\sim s_2$
if and only if
![]() ${\rm ord}_p([s_1]-[s_2])\geq D_p$
. Let
${\rm ord}_p([s_1]-[s_2])\geq D_p$
. Let
![]() $L\in {\rm Pic}(\Sigma )$
, and define the following subspaces of
$L\in {\rm Pic}(\Sigma )$
, and define the following subspaces of
![]() $H^0(\Lambda,L^2K)$
:
$H^0(\Lambda,L^2K)$
:
 \begin{align*} \mathcal{V}( D,L)& :=\{s\in H^0(\Lambda,L^2K)\mid {\rm ord}_p(s)=\Lambda _p-D_p,\;{\rm if}\;D_p\gt 0;\;s|_p=0,\;{\rm if}\;D_p=0\};\\ \mathcal{W}( D,L) & =\{s\in H^0(\Lambda,L^2K)\mid s|_{{\rm supp\;}(\Lambda -D)}=0\}. \end{align*}
\begin{align*} \mathcal{V}( D,L)& :=\{s\in H^0(\Lambda,L^2K)\mid {\rm ord}_p(s)=\Lambda _p-D_p,\;{\rm if}\;D_p\gt 0;\;s|_p=0,\;{\rm if}\;D_p=0\};\\ \mathcal{W}( D,L) & =\{s\in H^0(\Lambda,L^2K)\mid s|_{{\rm supp\;}(\Lambda -D)}=0\}. \end{align*}
One checks that
![]() $\mathcal{W}(D,L)=\cup _{D^{\prime}\leq D}\mathcal{V}(D^{\prime},L)$
. Moreover, the space
$\mathcal{W}(D,L)=\cup _{D^{\prime}\leq D}\mathcal{V}(D^{\prime},L)$
. Moreover, the space
![]() $\mathcal{V}( D,L)$
is a linear subspace of
$\mathcal{V}( D,L)$
is a linear subspace of
![]() $H^0(\Lambda,L^2K)$
with a hyperplane removed. In addition,
$H^0(\Lambda,L^2K)$
with a hyperplane removed. In addition,
![]() $\mathbb{C}^{\ast }$
acts on
$\mathbb{C}^{\ast }$
acts on
![]() $\mathcal{V}( D,L)$
by multiplication, and
$\mathcal{V}( D,L)$
by multiplication, and
![]() $\dim (\mathcal{V}( D,L)/\mathbb{C}^{\ast })=\deg ( D)-1$
.
$\dim (\mathcal{V}( D,L)/\mathbb{C}^{\ast })=\deg ( D)-1$
.
We define the fibrations
such that for
![]() $L\in {\rm Pic}^m(\Sigma )$
, the fibres are
$L\in {\rm Pic}^m(\Sigma )$
, the fibres are
![]() $\mathcal{V}(D,L)$
and
$\mathcal{V}(D,L)$
and
![]() $\mathcal{W}(D,L)$
.
$\mathcal{W}(D,L)$
.
7.2.1 Algebraic data from the extension
The Higgs bundle
![]() $(\mathcal{E},\varphi )$
can be understood in terms of an extension. Since
$(\mathcal{E},\varphi )$
can be understood in terms of an extension. Since
![]() $\det (\mathcal{E})=\mathcal{O}$
, we have the exact sequence
$\det (\mathcal{E})=\mathcal{O}$
, we have the exact sequence
For each
![]() $p\in Z$
, with
$p\in Z$
, with
![]() $U\subset \Sigma$
a neighbourhood of
$U\subset \Sigma$
a neighbourhood of
![]() $p$
,
$p$
,
![]() $(\mathcal{E},\varphi )$
can be written in terms of a splitting of
$(\mathcal{E},\varphi )$
can be written in terms of a splitting of
![]() $\mathcal{C}^{\infty }$
bundles
$\mathcal{C}^{\infty }$
bundles
Now consider
![]() $\varphi \bigr |_\Lambda$
. Because the induced morphisms
$\varphi \bigr |_\Lambda$
. Because the induced morphisms
both vanish, we obtain the map
![]() $s :L_+^{-1}|_{\Lambda }\simeq (\mathcal{E}/L_+)\bigr |_\Lambda \to L_+K|_{\Lambda }$
or, equivalently, a section
$s :L_+^{-1}|_{\Lambda }\simeq (\mathcal{E}/L_+)\bigr |_\Lambda \to L_+K|_{\Lambda }$
or, equivalently, a section
![]() $s\in H^0(\Lambda,L_+^2K).$
Moreover, by [Reference Gothen and OliveiraGO13, Lemma 7.12],
$s\in H^0(\Lambda,L_+^2K).$
Moreover, by [Reference Gothen and OliveiraGO13, Lemma 7.12],
![]() ${\rm Div}(s)=\Lambda -D$
, where
${\rm Div}(s)=\Lambda -D$
, where
![]() ${\rm Div}(s)$
is the divisor defined by zeros of
${\rm Div}(s)$
is the divisor defined by zeros of
![]() $s$
. Therefore, given any
$s$
. Therefore, given any
![]() $(\mathcal{E},\varphi )\in \mathcal{M}_q$
, we obtain an
$(\mathcal{E},\varphi )\in \mathcal{M}_q$
, we obtain an
![]() $L\in {\rm Pic}^{m}(\Sigma )$
and an element in
$L\in {\rm Pic}^{m}(\Sigma )$
and an element in
![]() $\mathcal{V}(D,L)$
. The stability condition implies that if
$\mathcal{V}(D,L)$
. The stability condition implies that if
![]() $0\leq D\leq \Lambda$
, we have
$0\leq D\leq \Lambda$
, we have
![]() $-\deg D\leq \deg L\leq 0.$
$-\deg D\leq \deg L\leq 0.$
7.2.2 Inverse construction
The inverse of the construction above also holds; for further details, see [Reference Gothen and OliveiraGO13, Sec. 7] and [Reference HornHor22a, Sec. 5]. Given
![]() $L\in {\rm Pic}^{m}(\Sigma )$
and
$L\in {\rm Pic}^{m}(\Sigma )$
and
![]() $s\in \mathcal{V}(D,L)$
, we define a Higgs bundle via extensions as follows: From
$s\in \mathcal{V}(D,L)$
, we define a Higgs bundle via extensions as follows: From
![]() $q=-\omega \otimes \omega,L$
, we have a short exact sequence of complexes of sheaves:
$q=-\omega \otimes \omega,L$
, we have a short exact sequence of complexes of sheaves:

where, for a section
![]() $s^{\prime}\in \Gamma (L^2)$
,
$s^{\prime}\in \Gamma (L^2)$
,
![]() $c(s^{\prime}):=\sqrt{-1}\omega s^{\prime}$
, and
$c(s^{\prime}):=\sqrt{-1}\omega s^{\prime}$
, and
![]() ${\rm res}(\Lambda )$
is the restriction map to the divisor
${\rm res}(\Lambda )$
is the restriction map to the divisor
![]() $\Lambda$
. The long exact sequence in hypercohomology implies that
$\Lambda$
. The long exact sequence in hypercohomology implies that
![]() ${\rm res}(\Lambda )$
induces an isomorphism
${\rm res}(\Lambda )$
induces an isomorphism
Moreover,
![]() ${\bf H}^1(C_2^{\ast })$
fits into an exact sequence
${\bf H}^1(C_2^{\ast })$
fits into an exact sequence
where
 \begin{align*} W_1 & = {\rm coker}\left (c : H^0(L^2)\longrightarrow H^0(L^2K)\right )\; \\ W_2 & = \ker \left (c : H^1(L^2)\longrightarrow H^1(L^2K)\right ) . \end{align*}
\begin{align*} W_1 & = {\rm coker}\left (c : H^0(L^2)\longrightarrow H^0(L^2K)\right )\; \\ W_2 & = \ker \left (c : H^1(L^2)\longrightarrow H^1(L^2K)\right ) . \end{align*}
Now
![]() $H^1(\Sigma,L^2)$
parameterises extensions
$H^1(\Sigma,L^2)$
parameterises extensions
Given
![]() $b\in W_2$
, we can find
$b\in W_2$
, we can find
![]() $c^{\prime}\in \Gamma (L^2K)$
,
$c^{\prime}\in \Gamma (L^2K)$
,
![]() $\bar{\partial }c^{\prime}=2b\omega$
and construct the Higgs bundle
$\bar{\partial }c^{\prime}=2b\omega$
and construct the Higgs bundle
For
![]() $0\leq D\leq \Lambda$
and
$0\leq D\leq \Lambda$
and
![]() $-\deg D\leq m\leq 0$
, the construction above defines the map
$-\deg D\leq m\leq 0$
, the construction above defines the map
where
![]() $[(\mathcal{E},\varphi )]$
is the S-equivalence class of the Higgs bundle constructed in (26) (note that for
$[(\mathcal{E},\varphi )]$
is the S-equivalence class of the Higgs bundle constructed in (26) (note that for
![]() $(b,c^{\prime})\neq (0,0)$
, the orbit of
$(b,c^{\prime})\neq (0,0)$
, the orbit of
![]() $(\mathcal{E},\varphi )$
is closed in the semistable locus if and only if
$(\mathcal{E},\varphi )$
is closed in the semistable locus if and only if
![]() $\deg (L)\neq 0$
). When
$\deg (L)\neq 0$
). When
![]() $ D=0$
,
$ D=0$
,
![]() $\mathcal{V}(\Lambda,L)=\{0\}$
and the image of
$\mathcal{V}(\Lambda,L)=\{0\}$
and the image of
![]() $\wp :\mathscr{V}(\Lambda,0)\to \mathcal{M}_q$
consists of the polystable Higgs bundles
$\wp :\mathscr{V}(\Lambda,0)\to \mathcal{M}_q$
consists of the polystable Higgs bundles
![]() $\mathcal{E}=L\oplus L^{-1},\;\varphi ={\rm diag}(\omega,-\omega )$
such that
$\mathcal{E}=L\oplus L^{-1},\;\varphi ={\rm diag}(\omega,-\omega )$
such that
![]() $L^2\cong \mathcal{O}_{\Sigma }$
.
$L^2\cong \mathcal{O}_{\Sigma }$
.
Theorem 7.1.
For
![]() $ 0\leq D\leq \Lambda$
and
$ 0\leq D\leq \Lambda$
and
![]() $-\deg ( D)\leq m_1\leq 0$
and the map
$-\deg ( D)\leq m_1\leq 0$
and the map
![]() $\wp :\mathscr{V}(D,m_1)\to \mathcal{M}_q$
, we have
$\wp :\mathscr{V}(D,m_1)\to \mathcal{M}_q$
, we have
-
(i) for
 $m_2=-\deg ( D)-m_1$
, we have
$m_2=-\deg ( D)-m_1$
, we have
 $\wp (\mathscr{V}(D,m_1))=\wp (\mathscr{V}(D,m_2))$
;
$\wp (\mathscr{V}(D,m_1))=\wp (\mathscr{V}(D,m_2))$
; -
(ii) for the
 $\mathbb{C}^{\ast }$
action on
$\mathbb{C}^{\ast }$
action on
 $\mathscr{V}(D,m_1)$
by multiplication, for
$\mathscr{V}(D,m_1)$
by multiplication, for
 $\xi \in \mathscr{V}(D,m_1)$
,
$\xi \in \mathscr{V}(D,m_1)$
,
 $\wp (\mathbb{C}^{\ast } \xi )=\wp (\xi )$
;
$\wp (\mathbb{C}^{\ast } \xi )=\wp (\xi )$
; -
(iii) when
 $m_1\neq -\frac 12\deg ( D),0,-\deg (D)$
,
$m_1\neq -\frac 12\deg ( D),0,-\deg (D)$
,
 $\wp :\mathscr{V}(D,m_1)/\mathbb{C}^{\ast } \to \mathcal{M}_q$
is an isomorphism onto its image;
$\wp :\mathscr{V}(D,m_1)/\mathbb{C}^{\ast } \to \mathcal{M}_q$
is an isomorphism onto its image;
-
(iv) when
 $m_1=-{1 \over 2}\deg ( D)$
,
$m_1=-{1 \over 2}\deg ( D)$
,
 $\wp :\mathscr{V}(D,m_1)/\mathbb{C}^{\ast } \to \mathcal{M}_q$
is a double-branched covering, which is branched along line bundles
$\wp :\mathscr{V}(D,m_1)/\mathbb{C}^{\ast } \to \mathcal{M}_q$
is a double-branched covering, which is branched along line bundles
 $L\in {\rm Pic}^{m_1}(\Sigma )$
such that
$L\in {\rm Pic}^{m_1}(\Sigma )$
such that
 $L^2\cong \mathcal{O}(- D)$
;
$L^2\cong \mathcal{O}(- D)$
; -
(v) when
 $ D=0$
, then
$ D=0$
, then
 $\wp :\mathscr{V}(\Lambda,0)\to \mathcal{M}_q$
is a double-branched covering, which is branched along
$\wp :\mathscr{V}(\Lambda,0)\to \mathcal{M}_q$
is a double-branched covering, which is branched along
 $L\in {\rm Pic}^0(\Sigma )$
such that
$L\in {\rm Pic}^0(\Sigma )$
such that
 $L^2\cong \mathcal{O};$
$L^2\cong \mathcal{O};$
-
(vi) when
 $m_1=0,-\deg (D)$
,
$m_1=0,-\deg (D)$
,
 $\wp :\mathscr{V}(\Lambda,0)\to \mathcal{M}_q$
is surjective but not injective. The image of
$\wp :\mathscr{V}(\Lambda,0)\to \mathcal{M}_q$
is surjective but not injective. The image of
 $\wp$
are all polystable Higgs bundles.
$\wp$
are all polystable Higgs bundles.
Remark 7.2. Parts
![]() $(iii)$
and
$(iii)$
and
![]() $(vi)$
of Theorem 7.1 are different from the statements in [Reference Gothen and OliveiraGO13, Theorem 7.7]. Because of the S-equivalence, when
$(vi)$
of Theorem 7.1 are different from the statements in [Reference Gothen and OliveiraGO13, Theorem 7.7]. Because of the S-equivalence, when
![]() $m_1=0,-\deg (D)$
, the map
$m_1=0,-\deg (D)$
, the map
![]() $\wp$
will not be injective. We thank the authors of [Reference Gothen and OliveiraGO13] for clarification of this point.
$\wp$
will not be injective. We thank the authors of [Reference Gothen and OliveiraGO13] for clarification of this point.
Example 7.3. When
![]() $g=2$
for
$g=2$
for
![]() $q=-\omega \otimes \omega$
, we can write
$q=-\omega \otimes \omega$
, we can write
![]() $\Lambda =p_1+p_2$
or
$\Lambda =p_1+p_2$
or
![]() $\Lambda=2p$
. In either case, the
$\Lambda=2p$
. In either case, the
![]() $\mathcal{M}_q^{{\rm st}}=\wp (\mathscr{V}(D,m))$
for
$\mathcal{M}_q^{{\rm st}}=\wp (\mathscr{V}(D,m))$
for
![]() $-\deg (D)\lt m\lt 0$
and
$-\deg (D)\lt m\lt 0$
and
![]() $0\leq D\leq \Lambda$
. Therefore,
$0\leq D\leq \Lambda$
. Therefore,
![]() $m=-1,\;D=\Lambda$
and
$m=-1,\;D=\Lambda$
and
![]() $\wp (\mathscr{V}(\Lambda,-1))=\mathcal{M}_q^{{\rm st}}$
. Moreover, generically, the map
$\wp (\mathscr{V}(\Lambda,-1))=\mathcal{M}_q^{{\rm st}}$
. Moreover, generically, the map
![]() $\wp :(\mathscr{V}(\Lambda,-1))/\mathbb{C}^{\ast }\to \mathcal{M}_q^{{\rm st}}$
is 2-to-1.
$\wp :(\mathscr{V}(\Lambda,-1))/\mathbb{C}^{\ast }\to \mathcal{M}_q^{{\rm st}}$
is 2-to-1.
7.3 The stratification of the singular fibre
We now present two stratifications of
![]() $\mathcal{M}_q$
. Recall that from any Higgs bundle
$\mathcal{M}_q$
. Recall that from any Higgs bundle
![]() $(\mathcal{E},\varphi )$
, we obtain two line bundles,
$(\mathcal{E},\varphi )$
, we obtain two line bundles,
![]() $L_{\pm }$
, and a divisor,
$L_{\pm }$
, and a divisor,
![]() $D$
. There are two different stratifications: one given by the divisor,
$D$
. There are two different stratifications: one given by the divisor,
![]() $D$
, and the other given by the degree of
$D$
, and the other given by the degree of
![]() $L_+$
.
$L_+$
.
7.3.1 Divisor stratification
We first discuss the stratification defined by the divisor. Indeed, using
![]() $D$
, decompose into strata:
$D$
, decompose into strata:
![]() $\mathcal{M}_q=\bigcup _{0\leq D\leq \Lambda }\mathcal{M}_{q,D}$
. Because the definition of
$\mathcal{M}_q=\bigcup _{0\leq D\leq \Lambda }\mathcal{M}_{q,D}$
. Because the definition of
![]() $L_{\pm }$
depends on the choice of the square root, there is no natural map from
$L_{\pm }$
depends on the choice of the square root, there is no natural map from
![]() $\mathcal{M}_{ D}$
to
$\mathcal{M}_{ D}$
to
![]() ${\rm Pic}(\Sigma)$
. Consider the following space:
${\rm Pic}(\Sigma)$
. Consider the following space:
![]() $\mathbb{V}_{ D}=\bigcup _{-\deg ( D)\leq m\leq 0}\mathscr{V}( D,m)$
. This forms a fibration:
$\mathbb{V}_{ D}=\bigcup _{-\deg ( D)\leq m\leq 0}\mathscr{V}( D,m)$
. This forms a fibration:
Moreover, for
![]() $L\in {\rm Pic}^{m}(\Sigma )$
, we have
$L\in {\rm Pic}^{m}(\Sigma )$
, we have
![]() $\tau ^{-1}(L)=\mathscr{V}( D,L)$
and
$\tau ^{-1}(L)=\mathscr{V}( D,L)$
and
![]() $\dim (\tau ^{-1}(L)/\mathbb{C}^{\ast })=\deg ( D)-1$
. By Theorem 7.1,
$\dim (\tau ^{-1}(L)/\mathbb{C}^{\ast })=\deg ( D)-1$
. By Theorem 7.1,
![]() $\wp |_{\mathbb{V}_{ D}}:\mathbb{V}_{ D}\to \mathcal{M}_{ D}$
is surjective. Since
$\wp |_{\mathbb{V}_{ D}}:\mathbb{V}_{ D}\to \mathcal{M}_{ D}$
is surjective. Since
generically,
![]() $\wp |_{\mathbb{V}_{ D}}$
is a 2-to-1 map.
$\wp |_{\mathbb{V}_{ D}}$
is a 2-to-1 map.
In summary, we obtain the following map, which characterises the singular fibre.
The top stratum is given by
![]() $D=\Lambda$
.
$D=\Lambda$
.
7.3.2 Degree stratification
We next introduce the stratification defined by degrees; this encodes how different divisor stratifications are glued together. For
![]() $-(2g-2)\leq m\leq 0$
and
$-(2g-2)\leq m\leq 0$
and
![]() $L\in {\rm Pic}^m(\Sigma )$
, define
$L\in {\rm Pic}^m(\Sigma )$
, define
![]() $\mathbb{W}(L):=\bigcup _{\deg D\geq -m}\mathcal{V}( D,L)$
. This set is connected, based on the definition and on [Reference Gothen and OliveiraGO13, Lemma 7.14]. Moreover, if we define
$\mathbb{W}(L):=\bigcup _{\deg D\geq -m}\mathcal{V}( D,L)$
. This set is connected, based on the definition and on [Reference Gothen and OliveiraGO13, Lemma 7.14]. Moreover, if we define
then we have
![]() $\wp (\mathbb{W})=\wp (\mathbb{V}).$
We should also note that although
$\wp (\mathbb{W})=\wp (\mathbb{V}).$
We should also note that although
![]() $\mathbb{W}_m\cap \mathbb{W}_n=\emptyset$
for any
$\mathbb{W}_m\cap \mathbb{W}_n=\emptyset$
for any
![]() $m\neq n$
,
$m\neq n$
,
![]() $\mathbb{W}$
is connected. As
$\mathbb{W}$
is connected. As
![]() $L_+,L_-$
are symmetric, by Theorem 7.1 we have
$L_+,L_-$
are symmetric, by Theorem 7.1 we have
which implies that for any integer
![]() $-(2g-2+m)\leq n\leq 0$
,
$-(2g-2+m)\leq n\leq 0$
,
![]() $\wp \mathbb{W}_m\cap \wp \mathbb{W}_n\neq \emptyset$
.
$\wp \mathbb{W}_m\cap \wp \mathbb{W}_n\neq \emptyset$
.
We now give an example of the degree stratification when
![]() $g=2$
.
$g=2$
.
Example 7.4. Suppose
![]() $\omega$
has only one zero with order 2. Then
$\omega$
has only one zero with order 2. Then
![]() $\Lambda=2p$
, and all possible divisors are
$\Lambda=2p$
, and all possible divisors are
![]() $D_2=2p,D_1=p,D_0=0$
. The degree stratification is
$D_2=2p,D_1=p,D_0=0$
. The degree stratification is
The image of
![]() $\wp (\mathscr{V}(D_2,-1))$
is stable;
$\wp (\mathscr{V}(D_2,-1))$
is stable;
![]() $\wp (\mathscr{V}(D_0,0))$
is polystable; and
$\wp (\mathscr{V}(D_0,0))$
is polystable; and
![]() $\wp (\mathscr{W}\setminus (\mathscr{V}(D_2,-1)\cup \mathscr{V}(D_0,0)))$
is semistable.
$\wp (\mathscr{W}\setminus (\mathscr{V}(D_2,-1)\cup \mathscr{V}(D_0,0)))$
is semistable.
Moreover, we have
![]() $\wp (\mathscr{V}(D_2,-2))=\wp (\mathscr{V}(D_2,0))$
and
$\wp (\mathscr{V}(D_2,-2))=\wp (\mathscr{V}(D_2,0))$
and
![]() $\wp (\mathscr{V}(D_1,-1))=\wp (\mathscr{V}(D_1,0))$
, and
$\wp (\mathscr{V}(D_1,-1))=\wp (\mathscr{V}(D_1,0))$
, and
![]() $\wp |_{\mathscr{V}(D_2,-1)}$
is a branched covering. Furthermore, we have
$\wp |_{\mathscr{V}(D_2,-1)}$
is a branched covering. Furthermore, we have
![]() $\wp (\mathscr{V}(D_2,-1))\cap \wp (\mathscr{V}(D_1,0))\neq 0$
and
$\wp (\mathscr{V}(D_2,-1))\cap \wp (\mathscr{V}(D_1,0))\neq 0$
and
![]() $\wp (\mathscr{V}(D_2,-1))\cap \wp (\mathscr{V}(D_0,0))=0$
.
$\wp (\mathscr{V}(D_2,-1))\cap \wp (\mathscr{V}(D_0,0))=0$
.
7.4 Algebraic Mochizuki map
Based on the study of the local rescaling properties of Higgs bundles, Mochizuki introduced a weight for each
![]() $p \in Z$
in [Reference MochizukiMoc16, Sec. 3]. To be more specific, let
$p \in Z$
in [Reference MochizukiMoc16, Sec. 3]. To be more specific, let
![]() $c$
be a real number. For each
$c$
be a real number. For each
![]() $p \in Z$
, the weight we consider is given by
$p \in Z$
, the weight we consider is given by
where
![]() ${\rm Div}(\omega )=\sum _p m_p p$
and
${\rm Div}(\omega )=\sum _p m_p p$
and
![]() $\ell _p$
is defined as in Section 7.1.1.
$\ell _p$
is defined as in Section 7.1.1.
By utilizing the global geometry of a Higgs bundle, we can uniquely determine the constant
![]() $c$
. We aim to choose the sign of
$c$
. We aim to choose the sign of
![]() $\omega$
such that
$\omega$
such that
![]() $d_+ \leq d_-$
.
$d_+ \leq d_-$
.
Lemma 7.4 [Reference MochizukiMoc16, Lemma 4.3].
If
![]() $(\mathcal{E},\varphi )$
is stable, then there exists a unique constant
$(\mathcal{E},\varphi )$
is stable, then there exists a unique constant
![]() $c\geq 0$
such that
$c\geq 0$
such that
Proof.
Since
![]() $(\mathcal{E},\varphi )$
is stable, we have
$(\mathcal{E},\varphi )$
is stable, we have
![]() $-\sum \ell _p\lt d_{\pm }\lt 0$
. We define the function
$-\sum \ell _p\lt d_{\pm }\lt 0$
. We define the function
which is strictly increasing. Moreover, for
![]() $c$
sufficiently large,
$c$
sufficiently large,
![]() $\chi _p(c)=\ell _p$
, and therefore
$\chi _p(c)=\ell _p$
, and therefore
![]() $f(c)=d_++\sum _p\ell _p=-d_-\gt 0$
. Additionally,
$f(c)=d_++\sum _p\ell _p=-d_-\gt 0$
. Additionally,
![]() $f(0)=d_++\sum _p (\ell _p/2)$
. Since
$f(0)=d_++\sum _p (\ell _p/2)$
. Since
![]() $d_+\leq d_-$
and
$d_+\leq d_-$
and
![]() $d_++d_-+\sum _p\ell _p=0$
, we obtain
$d_++d_-+\sum _p\ell _p=0$
, we obtain
![]() $f(0)\leq 0$
. The monotonicity of
$f(0)\leq 0$
. The monotonicity of
![]() $f$
implies the existence of
$f$
implies the existence of
![]() $c_0$
such that
$c_0$
such that
![]() $f(c_0)=0$
.
$f(c_0)=0$
.
From this construction, if
![]() $d_+\leq d_-$
, two weighted bundles
$d_+\leq d_-$
, two weighted bundles
![]() $(L_+,\chi _p(c_0))$
and
$(L_+,\chi _p(c_0))$
and
![]() $(L_{-},\ell _p-\chi _p(c_0))$
are obtained with weights
$(L_{-},\ell _p-\chi _p(c_0))$
are obtained with weights
![]() $\chi _p(c_0)$
and
$\chi _p(c_0)$
and
![]() $\ell _p-\chi _p(c_0)$
at each
$\ell _p-\chi _p(c_0)$
at each
![]() $p\in Z$
, respectively. On the other hand, if
$p\in Z$
, respectively. On the other hand, if
![]() $d_+\geq d_-$
, by symmetry, weighted bundles
$d_+\geq d_-$
, by symmetry, weighted bundles
![]() $(L_+,\ell _p-\chi _p(c_0))$
and
$(L_+,\ell _p-\chi _p(c_0))$
and
![]() $(L_-,\chi _p(c_0))$
are obtained. When
$(L_-,\chi _p(c_0))$
are obtained. When
![]() $(\mathcal{E},\varphi )$
is strictly semistable, S-equivalent to
$(\mathcal{E},\varphi )$
is strictly semistable, S-equivalent to
![]() $(L,\omega )\oplus (L^{-1},-\omega )$
, then we would like to consider the weighted bundles
$(L,\omega )\oplus (L^{-1},-\omega )$
, then we would like to consider the weighted bundles
![]() $(L,0)\oplus (L^{-1},0)$
with weight zero.
$(L,0)\oplus (L^{-1},0)$
with weight zero.
Next, we define the algebraic Mochizuki map. Let
![]() $\mathscr{F}_{\pm }(\Sigma )$
be the space of rank 1 degree zero-filtered bundles on
$\mathscr{F}_{\pm }(\Sigma )$
be the space of rank 1 degree zero-filtered bundles on
![]() $\Sigma$
, and let
$\Sigma$
, and let
![]() $\mathscr{F}_2(\Sigma ):=\mathscr{F}_+(\Sigma )\times \mathscr{F}_-(\Sigma )$
be the direct product. Fix a choice of
$\mathscr{F}_2(\Sigma ):=\mathscr{F}_+(\Sigma )\times \mathscr{F}_-(\Sigma )$
be the direct product. Fix a choice of
![]() $\omega$
. Then from any Higgs bundle
$\omega$
. Then from any Higgs bundle
![]() $(\mathcal{E},\varphi )$
, we obtain the subbundles
$(\mathcal{E},\varphi )$
, we obtain the subbundles
![]() $L_{\pm }$
with degree
$L_{\pm }$
with degree
![]() $d_{\pm }$
and define the algebraic Mochizuki map:
$d_{\pm }$
and define the algebraic Mochizuki map:
 \begin{align*} & \Theta ^{{\rm Moc}} :\mathcal{M}_q\longrightarrow \mathscr{F}_2(\Sigma ),\\ & \Theta ^{{\rm Moc}} (\mathcal{E},\varphi ):=\left \{\begin{matrix} \mathcal{F}_{\ast }(L_+,\chi _p(c_0))\oplus \mathcal{F}_{\ast }(L_-,\ell _p-\chi _p(c_0)),\;{\rm if}\;d_+\leq d_-\\ \mathcal{F}_{\ast }(L_+,\ell _p-\chi _p(c_0))\oplus \mathcal{F}_{\ast }(L_-,\chi _p(c_0)),\;{\rm if}\;d_-\leq d_+ \end{matrix}\right.,\;(\mathcal{E},\varphi )\;{\rm stable},\\ & \Theta ^{{\rm Moc}} (\mathcal{E},\varphi ):=\mathcal{F}_{\ast }(L,0)\oplus \mathcal{F}_{\ast }(L^{-1},0),\;(\mathcal{E},\varphi )\;{\rm semistable}. \end{align*}
\begin{align*} & \Theta ^{{\rm Moc}} :\mathcal{M}_q\longrightarrow \mathscr{F}_2(\Sigma ),\\ & \Theta ^{{\rm Moc}} (\mathcal{E},\varphi ):=\left \{\begin{matrix} \mathcal{F}_{\ast }(L_+,\chi _p(c_0))\oplus \mathcal{F}_{\ast }(L_-,\ell _p-\chi _p(c_0)),\;{\rm if}\;d_+\leq d_-\\ \mathcal{F}_{\ast }(L_+,\ell _p-\chi _p(c_0))\oplus \mathcal{F}_{\ast }(L_-,\chi _p(c_0)),\;{\rm if}\;d_-\leq d_+ \end{matrix}\right.,\;(\mathcal{E},\varphi )\;{\rm stable},\\ & \Theta ^{{\rm Moc}} (\mathcal{E},\varphi ):=\mathcal{F}_{\ast }(L,0)\oplus \mathcal{F}_{\ast }(L^{-1},0),\;(\mathcal{E},\varphi )\;{\rm semistable}. \end{align*}
We list some properties of this map:
Proposition 7.5.
For
![]() $\Theta ^{{\rm Moc}}$
, we have:
$\Theta ^{{\rm Moc}}$
, we have:
-
(i) for each
 $\mathscr{V}( D,m)$
with
$\mathscr{V}( D,m)$
with
 $0\leq D\leq \Lambda$
,
$0\leq D\leq \Lambda$
,
 $-\deg ( D)\leq m\leq 0$
,
$-\deg ( D)\leq m\leq 0$
,
 $\Theta ^{{\rm Moc}}|_{\wp (\mathscr{V}( D,m))}$
is continuous;
$\Theta ^{{\rm Moc}}|_{\wp (\mathscr{V}( D,m))}$
is continuous;
-
(ii) for
 $i=1,2$
and
$i=1,2$
and
 $s_i\in \mathbb{V}_D$
with
$s_i\in \mathbb{V}_D$
with
 $(\mathcal{E}_i,\varphi _i):=\wp (s_i)$
, suppose
$(\mathcal{E}_i,\varphi _i):=\wp (s_i)$
, suppose
 $\tau (s_1)=\tau (s_2)$
; then
$\tau (s_1)=\tau (s_2)$
; then
 $\Theta ^{{\rm Moc}}(\mathcal{E}_1,\varphi _1)=\Theta ^{{\rm Moc}}(\mathcal{E}_2,\varphi _2)$
. In particular,
$\Theta ^{{\rm Moc}}(\mathcal{E}_1,\varphi _1)=\Theta ^{{\rm Moc}}(\mathcal{E}_2,\varphi _2)$
. In particular,
 $\Theta ^{{\rm Moc}}$
is not injective.
$\Theta ^{{\rm Moc}}$
is not injective.
Proof. The proof follows directly from the definition.
A Higgs bundle
![]() $(\mathcal{E},\varphi ) \in \mathcal{M}_q$
is called ‘exotic’ if the constant
$(\mathcal{E},\varphi ) \in \mathcal{M}_q$
is called ‘exotic’ if the constant
![]() $c$
in Lemma 7.5 satisfies
$c$
in Lemma 7.5 satisfies
![]() $c \neq 0$
. This new behavior appears only in the Hitchin fibre with a reducible spectral curve.
$c \neq 0$
. This new behavior appears only in the Hitchin fibre with a reducible spectral curve.
Proposition 7.7.
A Higgs bundle
![]() $(\mathcal{E},\varphi )$
is not exotic if and only if its corresponding degrees satisfy
$(\mathcal{E},\varphi )$
is not exotic if and only if its corresponding degrees satisfy
![]() $d_+=d_-$
.
$d_+=d_-$
.
Proof. This is straightforward from the definition and from Lemma 7.4.
7.5 Discontinuous behavior
In this subsection, we study the discontinuous behavior of
![]() $\Theta ^{{\rm Moc}}$
. Consider a sequence of algebraic data
$\Theta ^{{\rm Moc}}$
. Consider a sequence of algebraic data
![]() $(L_i,q_i)\in \mathbb{W}_m$
, where
$(L_i,q_i)\in \mathbb{W}_m$
, where
![]() $L_i\in {\rm Pic}^m$
and
$L_i\in {\rm Pic}^m$
and
![]() $q_i\in \mathscr{V}(D,L_i)$
. We assume that
$q_i\in \mathscr{V}(D,L_i)$
. We assume that
![]() $\lim _{i\to \infty }L_i=L_{\infty }$
in
$\lim _{i\to \infty }L_i=L_{\infty }$
in
![]() ${\rm Pic}^m$
and
${\rm Pic}^m$
and
![]() $\lim _{i\to \infty }q_i=q_{\infty }\in \mathscr{V}(D_{\infty },L)$
, for
$\lim _{i\to \infty }q_i=q_{\infty }\in \mathscr{V}(D_{\infty },L)$
, for
![]() $D_{\infty }\neq D$
. As the space
$D_{\infty }\neq D$
. As the space
![]() $\bigcup _{\deg D^{\prime}\geq -m}\mathscr{V}(D^{\prime},m)$
is connected, we can always find such a sequence.
$\bigcup _{\deg D^{\prime}\geq -m}\mathscr{V}(D^{\prime},m)$
is connected, we can always find such a sequence.
Let
![]() $L_+^i:=L_i$
and
$L_+^i:=L_i$
and
![]() $L_-^i:=L_i^{-1}\otimes \mathcal{O}(-D)$
. By Lemma 7.5 the weight function, which we denote by
$L_-^i:=L_i^{-1}\otimes \mathcal{O}(-D)$
. By Lemma 7.5 the weight function, which we denote by
![]() $\chi _{\pm }$
, is independent of
$\chi _{\pm }$
, is independent of
![]() $i$
. In addition, we have
$i$
. In addition, we have
For
![]() $(L_{\infty },q_{\infty }\in \mathscr{V}(D_{\infty },L))$
, let
$(L_{\infty },q_{\infty }\in \mathscr{V}(D_{\infty },L))$
, let
![]() $\chi ^{\infty }_{\pm }$
be the corresponding weights. These depend on
$\chi ^{\infty }_{\pm }$
be the corresponding weights. These depend on
![]() $D_{\infty }$
and
$D_{\infty }$
and
![]() $m$
. Then
$m$
. Then
Therefore, we obtain
 \begin{align} & \lim _{i\to \infty }\Theta ^{{\rm Moc}}\circ \wp (L_i,q_i)\nonumber\\ & = \Theta ^{{\rm Moc}}\circ \wp (L_{\infty },q_{\infty })\otimes (\mathcal{F}_{\ast }(\mathcal{O},\chi _+-\chi _+^{\infty })\oplus \mathcal{F}_{\ast }(\mathcal{O}( D_{\infty }- D),\chi _-\chi _-^{\infty })). \end{align}
\begin{align} & \lim _{i\to \infty }\Theta ^{{\rm Moc}}\circ \wp (L_i,q_i)\nonumber\\ & = \Theta ^{{\rm Moc}}\circ \wp (L_{\infty },q_{\infty })\otimes (\mathcal{F}_{\ast }(\mathcal{O},\chi _+-\chi _+^{\infty })\oplus \mathcal{F}_{\ast }(\mathcal{O}( D_{\infty }- D),\chi _-\chi _-^{\infty })). \end{align}
Proposition 7.7.
When
![]() $g\geq 3$
, there exists a sequence
$g\geq 3$
, there exists a sequence
![]() $(\mathcal{E}_i,\varphi _i)\in \mathcal{M}_q$
of stable Higgs bundles with stable limit
$(\mathcal{E}_i,\varphi _i)\in \mathcal{M}_q$
of stable Higgs bundles with stable limit
![]() $(\mathcal{E}_{\infty },\varphi _{\infty })=\lim _{i\to \infty }(\mathcal{E}_i,\varphi _i)$
such that
$(\mathcal{E}_{\infty },\varphi _{\infty })=\lim _{i\to \infty }(\mathcal{E}_i,\varphi _i)$
such that
Proof.
Choose
![]() $ D=\Lambda$
and
$ D=\Lambda$
and
![]() $d_+=-(g-1)$
with
$d_+=-(g-1)$
with
![]() $L_i=L\in {\rm Pic}^{d_+}(\Sigma )$
, and study the degenerate behavior for a family
$L_i=L\in {\rm Pic}^{d_+}(\Sigma )$
, and study the degenerate behavior for a family
![]() $q_i\in \mathcal{V}(\Lambda,L)$
that converges to
$q_i\in \mathcal{V}(\Lambda,L)$
that converges to
![]() $q_{\infty }\in \mathscr{V}( D_{\infty },L)$
. Here,
$q_{\infty }\in \mathscr{V}( D_{\infty },L)$
. Here,
![]() $D_{\infty }$
satisfies
$D_{\infty }$
satisfies
![]() $D_{\infty }\leq D$
and
$D_{\infty }\leq D$
and
![]() $\deg (D_{\infty })=\deg (D)-1$
. As
$\deg (D_{\infty })=\deg (D)-1$
. As
![]() $q_i$
lies in the top stratum, we can always find such a family. Take
$q_i$
lies in the top stratum, we can always find such a family. Take
![]() $(\mathcal{E}_i,\varphi _i)=\wp (L_i,q_i)$
and
$(\mathcal{E}_i,\varphi _i)=\wp (L_i,q_i)$
and
![]() $(\mathcal{E}_{\infty },\varphi _{\infty })=\wp (L,q_{\infty })$
. When
$(\mathcal{E}_{\infty },\varphi _{\infty })=\wp (L,q_{\infty })$
. When
![]() $g\geq 3$
, we have
$g\geq 3$
, we have
![]() $-\deg (D_{\infty })\lt d_+\leq -\frac 12\deg (D_{\infty })$
, which implies that
$-\deg (D_{\infty })\lt d_+\leq -\frac 12\deg (D_{\infty })$
, which implies that
![]() $(\mathcal{E}_{\infty },\varphi _{\infty })$
is a stable Higgs bundle.
$(\mathcal{E}_{\infty },\varphi _{\infty })$
is a stable Higgs bundle.
Write
![]() $D=\sum _p\ell _p$
. As
$D=\sum _p\ell _p$
. As
![]() $(\mathcal{E}_i,\varphi _i)$
is nonexotic, the weights will be
$(\mathcal{E}_i,\varphi _i)$
is nonexotic, the weights will be
![]() $\chi _+(p)=\chi _-(p)=\ell _p/2$
. However, as
$\chi _+(p)=\chi _-(p)=\ell _p/2$
. However, as
![]() $\deg (D_{\infty })\neq 2d_+$
,
$\deg (D_{\infty })\neq 2d_+$
,
![]() $(\mathcal{E}_{\infty },\varphi _{\infty })$
is exotic. By Proposition 7.6, if we write
$(\mathcal{E}_{\infty },\varphi _{\infty })$
is exotic. By Proposition 7.6, if we write
![]() $\chi _{\pm }^{\infty }(p)$
for the weight functions with corresponding constant
$\chi _{\pm }^{\infty }(p)$
for the weight functions with corresponding constant
![]() $c$
, then
$c$
, then
![]() $c\gt 0$
. Therefore, for
$c\gt 0$
. Therefore, for
![]() $p\neq p_0$
, we have
$p\neq p_0$
, we have
![]() $\chi ^{\infty }_+(p)=(m_p+1)c+m_p/2\gt m_p/2=\chi _+(p)$
. By (28),
$\chi ^{\infty }_+(p)=(m_p+1)c+m_p/2\gt m_p/2=\chi _+(p)$
. By (28),
![]() $\lim _{i\to \infty }\Theta ^{{\rm Moc}}(\mathcal{E}_i,\varphi _i)\neq \Theta ^{{\rm Moc}}(\mathcal{E}_{\infty },\varphi _{\infty })$
.
$\lim _{i\to \infty }\Theta ^{{\rm Moc}}(\mathcal{E}_i,\varphi _i)\neq \Theta ^{{\rm Moc}}(\mathcal{E}_{\infty },\varphi _{\infty })$
.
When
![]() $g=2$
, the stratification is simpler, and we have the following:
$g=2$
, the stratification is simpler, and we have the following:
Proposition 7.8.
When
![]() $g=2$
, the following holds:
$g=2$
, the following holds:
-
(i) Suppose
 $\Lambda =p_1+p_2$
for
$\Lambda =p_1+p_2$
for
 $p_1\neq p_2$
; then
$p_1\neq p_2$
; then
 $\Theta ^{{\rm Moc}}|_{\mathcal{M}_q^{{\rm st}}}$
is continuous. Moreover, there exists a sequence of stable Higgs bundles
$\Theta ^{{\rm Moc}}|_{\mathcal{M}_q^{{\rm st}}}$
is continuous. Moreover, there exists a sequence of stable Higgs bundles
 $(\mathcal{E}_i,\varphi _i)\in \mathcal{M}_q$
where the limit
$(\mathcal{E}_i,\varphi _i)\in \mathcal{M}_q$
where the limit
 $(\mathcal{E}_{\infty },\varphi _{\infty })=\lim _{i\to \infty }(\mathcal{E}_i,\varphi _i)$
is semistable and where
$(\mathcal{E}_{\infty },\varphi _{\infty })=\lim _{i\to \infty }(\mathcal{E}_i,\varphi _i)$
is semistable and where
 $\gamma (0)$
is also semistable; furthermore
$\gamma (0)$
is also semistable; furthermore
 \begin{align*} \lim _{i\to \infty }\Theta ^{\mathrm {Moc}}(\mathcal {E}_i,\varphi _i)\neq \Theta ^{\mathrm {Moc}}(\mathcal {E}_{\infty },\varphi _{\infty }). \end{align*}
\begin{align*} \lim _{i\to \infty }\Theta ^{\mathrm {Moc}}(\mathcal {E}_i,\varphi _i)\neq \Theta ^{\mathrm {Moc}}(\mathcal {E}_{\infty },\varphi _{\infty }). \end{align*}
-
(ii) Suppose
 $\Lambda=2p$
. Then
$\Lambda=2p$
. Then
 $\Theta ^{{\rm Moc}}|_{\mathcal{M}_q^{{\rm st}}}$
is continuous.
$\Theta ^{{\rm Moc}}|_{\mathcal{M}_q^{{\rm st}}}$
is continuous.
Proof.
For (i), suppose
![]() $\Lambda =p_1+p_2$
; then by Example 7.2, we have
$\Lambda =p_1+p_2$
; then by Example 7.2, we have
![]() $\mathcal{M}_q^{{\rm st}}=\wp (\mathscr{V}(\Lambda,-1))$
. By Proposition 7.6,
$\mathcal{M}_q^{{\rm st}}=\wp (\mathscr{V}(\Lambda,-1))$
. By Proposition 7.6,
![]() $\Theta ^{{\rm Moc}}_q|_{\mathcal{M}_q^{{\rm st}}}$
is continuous. However, for semistable elements, other strata must be taken into consideration. Take
$\Theta ^{{\rm Moc}}_q|_{\mathcal{M}_q^{{\rm st}}}$
is continuous. However, for semistable elements, other strata must be taken into consideration. Take
![]() $L\in {\rm Pic}^{-1}(\Sigma )$
and
$L\in {\rm Pic}^{-1}(\Sigma )$
and
![]() $q_i\in \mathcal{V}(\Lambda,L)$
such that
$q_i\in \mathcal{V}(\Lambda,L)$
such that
![]() $q_i$
converges to
$q_i$
converges to
![]() $q_{\infty }\in \mathcal{V}(p_1,L)$
. We define
$q_{\infty }\in \mathcal{V}(p_1,L)$
. We define
![]() $(\mathcal{E}_i,\varphi _i)=\wp (L,q_i)$
and
$(\mathcal{E}_i,\varphi _i)=\wp (L,q_i)$
and
![]() $(\mathcal{E}_{\infty },\varphi _{\infty })=\wp (L,q_{\infty })$
. For each
$(\mathcal{E}_{\infty },\varphi _{\infty })=\wp (L,q_{\infty })$
. For each
![]() $i$
,
$i$
,
Moreover, we have
For (ii), by Example 7.3,
![]() $\wp (\mathscr{V}(D_2,-1))=\mathcal{M}_q^{{\rm st}}$
, and by Proposition 7.5,
$\wp (\mathscr{V}(D_2,-1))=\mathcal{M}_q^{{\rm st}}$
, and by Proposition 7.5,
![]() $\Theta ^{{\rm Moc}}_q|_{\mathcal{M}_q^{{\rm st}}}$
is continuous. We now consider the behavior of the filtered bundle when crossing the divisors.
$\Theta ^{{\rm Moc}}_q|_{\mathcal{M}_q^{{\rm st}}}$
is continuous. We now consider the behavior of the filtered bundle when crossing the divisors.
7.6 The analytic Mochizuki map and limiting configurations
In this subsection, we construct the analytic Mochizuki map for the Hitchin fibre with a reducible spectral curve. We also introduce the convergence theorem of Mochizuki as stated in [Reference MochizukiMoc16] and examine the discontinuous behavior of the analytic Mochizuki map.
thus
![]() $\Theta ^{{\rm Moc}}(\mathcal{E},\varphi )=\mathcal{F}_{\ast }(L_+,\chi _+)\oplus \mathcal{L}_-(L_-,\chi _-)\in \mathcal{F}_2(\Sigma )$
. Via the nonabelian Hodge correspondence for filtered bundles, we obtain two Hermitian metrics
$\Theta ^{{\rm Moc}}(\mathcal{E},\varphi )=\mathcal{F}_{\ast }(L_+,\chi _+)\oplus \mathcal{L}_-(L_-,\chi _-)\in \mathcal{F}_2(\Sigma )$
. Via the nonabelian Hodge correspondence for filtered bundles, we obtain two Hermitian metrics
![]() $h^{{\rm Lim}}_{\pm }$
with corresponding Chern connections
$h^{{\rm Lim}}_{\pm }$
with corresponding Chern connections
![]() $A_{h^{{\rm Lim}}_{\pm }}$
. These metrics satisfy the following proposition:
$A_{h^{{\rm Lim}}_{\pm }}$
. These metrics satisfy the following proposition:
Proposition 7.9.
The metrics
![]() $h_{\pm }^{{\rm Lim}}$
over
$h_{\pm }^{{\rm Lim}}$
over
![]() $L_{\pm }$
satisfy
$L_{\pm }$
satisfy
-
i)
 $F_{A_{h^{{\rm Lim}}_{\pm }}}=0$
and
$F_{A_{h^{{\rm Lim}}_{\pm }}}=0$
and
 $h_+^{{\rm Lim}}h_-^{{\rm Lim}}=1$
;
$h_+^{{\rm Lim}}h_-^{{\rm Lim}}=1$
; -
ii) for every
 $p\in \Sigma$
, there exists an open neighbourhood
$p\in \Sigma$
, there exists an open neighbourhood
 $(U,z)$
with
$(U,z)$
with
 $P=\{z=0\}$
such that
$P=\{z=0\}$
such that
 $|z|^{-2\chi _p(c_0)}h_{+}^{{\rm Lim}}$
and
$|z|^{-2\chi _p(c_0)}h_{+}^{{\rm Lim}}$
and
 $|z|^{2\chi _p(c_0)+2l_P}h_-^{{\rm Lim}}$
extend smoothly to
$|z|^{2\chi _p(c_0)+2l_P}h_-^{{\rm Lim}}$
extend smoothly to
 $L_{\pm }|_U$
.
$L_{\pm }|_U$
.
Now,
![]() $H^{{\rm Lim}}:=h_+^{{\rm Lim}} \oplus h_-^{{\rm Lim}}$
is a metric on
$H^{{\rm Lim}}:=h_+^{{\rm Lim}} \oplus h_-^{{\rm Lim}}$
is a metric on
![]() $\mathcal{E}_0$
that induces a metric on
$\mathcal{E}_0$
that induces a metric on
![]() $(\mathcal{E},\varphi )|_{\Sigma \setminus Z}$
because
$(\mathcal{E},\varphi )|_{\Sigma \setminus Z}$
because
![]() $(\mathcal{E},\varphi )|_{\Sigma \setminus Z} \cong (\mathcal{E}_0,\varphi _0)|_{\Sigma \setminus Z}$
. Let
$(\mathcal{E},\varphi )|_{\Sigma \setminus Z} \cong (\mathcal{E}_0,\varphi _0)|_{\Sigma \setminus Z}$
. Let
![]() $(A^{{\rm Lim}},\phi ^{{\rm Lim}})$
be the Chern connection defined by
$(A^{{\rm Lim}},\phi ^{{\rm Lim}})$
be the Chern connection defined by
![]() $(\mathcal{E},\varphi,H^{{\rm Lim}})$
over
$(\mathcal{E},\varphi,H^{{\rm Lim}})$
over
![]() $\Sigma \setminus Z$
. Then
$\Sigma \setminus Z$
. Then
![]() $(A^{{\rm Lim}},\phi ^{{\rm Lim}})$
is a limiting configuration that satisfies the decoupled Hitchin equations (9). The analytic Mochizuki map
$(A^{{\rm Lim}},\phi ^{{\rm Lim}})$
is a limiting configuration that satisfies the decoupled Hitchin equations (9). The analytic Mochizuki map
![]() $\Upsilon ^{{\rm Moc}}$
is defined as
$\Upsilon ^{{\rm Moc}}$
is defined as
Note that
![]() $H^{{\rm Lim}}$
is not unique: For any constant
$H^{{\rm Lim}}$
is not unique: For any constant
![]() $c$
, the metric
$c$
, the metric
![]() $c h_+^{{\rm Lim}} \oplus c^{-1} h_-^{{\rm Lim}}$
defines the same Chern connection as
$c h_+^{{\rm Lim}} \oplus c^{-1} h_-^{{\rm Lim}}$
defines the same Chern connection as
![]() $H^{{\rm Lim}}$
. In any case, the map
$H^{{\rm Lim}}$
. In any case, the map
![]() $\Upsilon ^{{\rm Moc}}$
is well-defined.
$\Upsilon ^{{\rm Moc}}$
is well-defined.
Suppose
![]() $(\mathcal{E},\varphi )$
is an S-equivalence class of a semistable Higgs bundle. Let
$(\mathcal{E},\varphi )$
is an S-equivalence class of a semistable Higgs bundle. Let
![]() $H_t$
be the harmonic metric for
$H_t$
be the harmonic metric for
![]() $(\mathcal{E},t\varphi )$
. For each constant
$(\mathcal{E},t\varphi )$
. For each constant
![]() $C\gt 0$
, define
$C\gt 0$
, define
![]() $\mu _C$
to be the automorphism of
$\mu _C$
to be the automorphism of
![]() $L_+ \oplus L_-$
given by
$L_+ \oplus L_-$
given by
![]() $\mu _C = C{\rm id}_{L_+} \oplus C^{-1} {\rm id}_{L_-}$
. As
$\mu _C = C{\rm id}_{L_+} \oplus C^{-1} {\rm id}_{L_-}$
. As
![]() $\mathcal{E} \cong L_+ \oplus L_-$
on
$\mathcal{E} \cong L_+ \oplus L_-$
on
![]() $\Sigma \setminus Z$
,
$\Sigma \setminus Z$
,
![]() $\mu _C^{\ast } H_t$
can be regarded as a metric on
$\mu _C^{\ast } H_t$
can be regarded as a metric on
![]() $\mathcal{E}|_{\Sigma \setminus Z}$
. Take any point
$\mathcal{E}|_{\Sigma \setminus Z}$
. Take any point
![]() $x \in \Sigma \setminus Z$
and a frame
$x \in \Sigma \setminus Z$
and a frame
![]() $e_x$
of
$e_x$
of
![]() $L_+|x$
, and define
$L_+|x$
, and define
 \begin{align*} C(x,t):=\biggl (\frac {h_{L_+}^{\mathrm {Lim}}(e_x,e_x)}{H_t(e_x,e_x)}\biggr )^{1/2}. \end{align*}
\begin{align*} C(x,t):=\biggl (\frac {h_{L_+}^{\mathrm {Lim}}(e_x,e_x)}{H_t(e_x,e_x)}\biggr )^{1/2}. \end{align*}
If we write
![]() $\nabla _t + t\phi _t$
as the corresponding flat connection of
$\nabla _t + t\phi _t$
as the corresponding flat connection of
![]() $(\mathcal{E},t\varphi )$
under the nonabelian Hodge correspondence, then
$(\mathcal{E},t\varphi )$
under the nonabelian Hodge correspondence, then
Theorem 7.10 [Reference MochizukiMoc16].
On any compact subset
![]() $K$
of
$K$
of
![]() $\Sigma \setminus Z$
,
$\Sigma \setminus Z$
,
![]() $\mu ^{\ast }_{C(x,t)}H_t$
converges smoothly to
$\mu ^{\ast }_{C(x,t)}H_t$
converges smoothly to
![]() $H^{{\rm Lim}}$
. In addition, we have
$H^{{\rm Lim}}$
. In addition, we have
![]() $\lim _{t\to 0}|(\nabla _t,\phi _t)-\Upsilon ^{{\rm Moc}}(\mathcal{E},\varphi )|_{\mathcal{C}^k(K)}=0.$
$\lim _{t\to 0}|(\nabla _t,\phi _t)-\Upsilon ^{{\rm Moc}}(\mathcal{E},\varphi )|_{\mathcal{C}^k(K)}=0.$
Comparing to the irreducible case Theorem 6.16, it is currently not known whether the convergence of
![]() $(\nabla _t,\phi _t)$
to
$(\nabla _t,\phi _t)$
to
![]() $\Upsilon ^{{\rm Moc}}(\mathcal{E},\varphi )$
is uniform.
$\Upsilon ^{{\rm Moc}}(\mathcal{E},\varphi )$
is uniform.
Propositions 7.7 and 7.8 now give
Theorem 7.11 (Theorem 1.3). When
![]() $g\geq 3$
,
$g\geq 3$
,
![]() $\Upsilon ^{{\rm Moc}}|_{\mathcal{M}_q^{{\rm st}}}$
is discontinuous, and when
$\Upsilon ^{{\rm Moc}}|_{\mathcal{M}_q^{{\rm st}}}$
is discontinuous, and when
![]() $g=2$
,
$g=2$
,
![]() $\Upsilon ^{{\rm Moc}}|_{\mathcal{M}_q^{{\rm st}}}$
is continuous.
$\Upsilon ^{{\rm Moc}}|_{\mathcal{M}_q^{{\rm st}}}$
is continuous.
8. The Compactified Kobayashi–Hitchin map
In this section, we define a compactified version of the Kobayashi–Hitchin map and prove the main theorem of our article. The Kobayashi–Hitchin map
![]() $\Xi$
is a homeomorphism between the Dolbeault moduli space
$\Xi$
is a homeomorphism between the Dolbeault moduli space
![]() $\mathcal{M}_{{\rm Dol}}$
and the Hitchin moduli space
$\mathcal{M}_{{\rm Dol}}$
and the Hitchin moduli space
![]() $\mathcal{M}_{{\rm Hit}}$
. We wish to extend this to a map
$\mathcal{M}_{{\rm Hit}}$
. We wish to extend this to a map
![]() $\overline{\Xi }$
from the compactified Dolbeault moduli space
$\overline{\Xi }$
from the compactified Dolbeault moduli space
![]() $\overline{\mathcal{M}}_{{\rm Dol}}$
to the compactification
$\overline{\mathcal{M}}_{{\rm Dol}}$
to the compactification
![]() $\overline{\mathcal{M}}_{{\rm Hit}}\subset \mathcal{M}_{{\rm Hit}}\cup \mathcal{M}_{{\rm Hit}}^{{\rm Lim}}$
of the Hitchin moduli space and then to study the properties of this extended map.
$\overline{\mathcal{M}}_{{\rm Hit}}\subset \mathcal{M}_{{\rm Hit}}\cup \mathcal{M}_{{\rm Hit}}^{{\rm Lim}}$
of the Hitchin moduli space and then to study the properties of this extended map.
8.1 The compactified Kobayashi–Hitchin map
We first summarise the results obtained above. By the construction in Section 4, there is an identification
![]() $\partial \overline{\mathcal{M}}_{{\rm Dol}}\cong (\mathcal{M}_{{\rm Dol}}\setminus \mathcal{H}^{-1}(0))/\mathbb{C}^{\ast }$
. Moreover, in (24)–(29), we have constructed the analytic Mochizuki map
$\partial \overline{\mathcal{M}}_{{\rm Dol}}\cong (\mathcal{M}_{{\rm Dol}}\setminus \mathcal{H}^{-1}(0))/\mathbb{C}^{\ast }$
. Moreover, in (24)–(29), we have constructed the analytic Mochizuki map
![]() $\Upsilon ^{{\rm Moc}}: \mathcal{M}_{{\rm Dol}}\setminus \mathcal{H}^{-1}(0)\to \mathcal{M}_{{\rm Hit}}^{{\rm Lim}}$
. Writing
$\Upsilon ^{{\rm Moc}}: \mathcal{M}_{{\rm Dol}}\setminus \mathcal{H}^{-1}(0)\to \mathcal{M}_{{\rm Hit}}^{{\rm Lim}}$
. Writing
for
![]() $w\in \mathbb{C}^{\ast }$
we then have
$w\in \mathbb{C}^{\ast }$
we then have
Hence,
![]() $\Upsilon ^{{\rm Moc}}$
descends to a map
$\Upsilon ^{{\rm Moc}}$
descends to a map
![]() $\partial \overline{\Xi }$
between
$\partial \overline{\Xi }$
between
![]() $\mathbb{C}^{\ast }$
orbits:
$\mathbb{C}^{\ast }$
orbits:
Together with the initial Kobayashi–Hitchin map
![]() $\Xi :\mathcal{M}_{{\rm Dol}}\to \mathcal{M}_{{\rm Hit}}$
, we obtain (2):
$\Xi :\mathcal{M}_{{\rm Dol}}\to \mathcal{M}_{{\rm Hit}}$
, we obtain (2):
Theorems 6.16 and 7.10 show that for a Higgs bundle
![]() $(\mathcal{E},\varphi )\in \mathcal{M}_{{\rm Dol}}\setminus \mathcal{H}^{-1}(0)$
and real
$(\mathcal{E},\varphi )\in \mathcal{M}_{{\rm Dol}}\setminus \mathcal{H}^{-1}(0)$
and real
![]() $t$
,
$t$
,
![]() $\lim _{t\to \infty }\Xi (\mathcal{E},t\varphi )=\partial \overline{\Xi }[(\mathcal{E},\varphi )/\mathbb{C}^{\ast }]$
. Thus the image of
$\lim _{t\to \infty }\Xi (\mathcal{E},t\varphi )=\partial \overline{\Xi }[(\mathcal{E},\varphi )/\mathbb{C}^{\ast }]$
. Thus the image of
![]() $\overline{\Xi }$
lies in
$\overline{\Xi }$
lies in
![]() $\overline{\mathcal{M}}_{{\rm Hit}}$
, the closure of
$\overline{\mathcal{M}}_{{\rm Hit}}$
, the closure of
![]() $\mathcal{M}_{{\rm Hit}}$
in
$\mathcal{M}_{{\rm Hit}}$
in
![]() $\mathcal{M}_{{\rm Hit}}\cup \mathcal{M}_{{\rm Dol}}\setminus \mathcal{H}^{-1}(0)$
. There are natural extensions
$\mathcal{M}_{{\rm Hit}}\cup \mathcal{M}_{{\rm Dol}}\setminus \mathcal{H}^{-1}(0)$
. There are natural extensions
![]() $\overline{\mathcal{H}}_{{\rm Dol}}:\overline{\mathcal{M}}_{{\rm Dol}}\to \overline{\mathcal{B}}$
and
$\overline{\mathcal{H}}_{{\rm Dol}}:\overline{\mathcal{M}}_{{\rm Dol}}\to \overline{\mathcal{B}}$
and
![]() $\overline{\mathcal{H}}_{{\rm Hit}}:\overline{\mathcal{M}}_{{\rm Hit}}\to \overline{\mathcal{B}}$
such that
$\overline{\mathcal{H}}_{{\rm Hit}}:\overline{\mathcal{M}}_{{\rm Hit}}\to \overline{\mathcal{B}}$
such that
![]() $\overline{\mathcal{H}}_{{\rm Hit}}\circ \overline{\Xi }=\overline{\mathcal{H}}_{{\rm Dol}}$
.
$\overline{\mathcal{H}}_{{\rm Hit}}\circ \overline{\Xi }=\overline{\mathcal{H}}_{{\rm Dol}}$
.
In summary, there are the following commutative diagrams:

We now turn to the analysis of some properties of the compactified Kobayashi–Hitchin map. Define
This is the compactified space of quadratic differentials with simple zeros. Let
![]() $\overline{\mathcal{B}}^{{\rm sing}}=\overline{\mathcal{B}}\setminus \overline{\mathcal{B}}^{{\rm reg}}$
be its complement. Additionally, define the open sets
$\overline{\mathcal{B}}^{{\rm sing}}=\overline{\mathcal{B}}\setminus \overline{\mathcal{B}}^{{\rm reg}}$
be its complement. Additionally, define the open sets
![]() $\overline{\mathcal{M}}_{{\rm Dol}}^{{\rm reg}}=\overline{\mathcal{H}}_{{\rm Dol}}^{-1}(\overline{\mathcal{B}}^{{\rm reg}})$
and
$\overline{\mathcal{M}}_{{\rm Dol}}^{{\rm reg}}=\overline{\mathcal{H}}_{{\rm Dol}}^{-1}(\overline{\mathcal{B}}^{{\rm reg}})$
and
![]() $\overline{\mathcal{M}}_{{\rm Hit}}^{{\rm reg}}=\overline{\mathcal{H}}_{{\rm Hit}}^{-1}(\overline{\mathcal{B}}^{{\rm reg}})$
as the collections of elements with regular spectral curves. Set
$\overline{\mathcal{M}}_{{\rm Hit}}^{{\rm reg}}=\overline{\mathcal{H}}_{{\rm Hit}}^{-1}(\overline{\mathcal{B}}^{{\rm reg}})$
as the collections of elements with regular spectral curves. Set
![]() $\overline{\mathcal{M}}_{{\rm Dol}}^{{\rm sing}}=\overline{\mathcal{H}}_{{\rm Dol}}^{-1}(\overline{\mathcal{B}}^{{\rm sing}})$
and
$\overline{\mathcal{M}}_{{\rm Dol}}^{{\rm sing}}=\overline{\mathcal{H}}_{{\rm Dol}}^{-1}(\overline{\mathcal{B}}^{{\rm sing}})$
and
![]() $\overline{\mathcal{M}}_{{\rm Hit}}^{{\rm sing}}=\overline{\mathcal{H}}_{{\rm Hit}}^{-1}(\overline{\mathcal{B}}^{{\rm sing}})$
to be the sets of singular fibres. We can then write
$\overline{\mathcal{M}}_{{\rm Hit}}^{{\rm sing}}=\overline{\mathcal{H}}_{{\rm Hit}}^{-1}(\overline{\mathcal{B}}^{{\rm sing}})$
to be the sets of singular fibres. We can then write
![]() $\overline{\Xi }=\overline{\Xi }^{{\rm reg}}\cup \overline{\Xi }^{{\rm sing}}$
, where
$\overline{\Xi }=\overline{\Xi }^{{\rm reg}}\cup \overline{\Xi }^{{\rm sing}}$
, where
Proposition 8.1.
The map
![]() $\overline{\Xi }^{{\rm reg}}:\overline{\mathcal{M}}_{{\rm Dol}}^{{\rm reg}}\to \overline{\mathcal{M}}_{{\rm Hit}}^{{\rm reg}}$
is bijective, whereas
$\overline{\Xi }^{{\rm reg}}:\overline{\mathcal{M}}_{{\rm Dol}}^{{\rm reg}}\to \overline{\mathcal{M}}_{{\rm Hit}}^{{\rm reg}}$
is bijective, whereas
![]() $\overline{\Xi }^{{\rm sing}}:\overline{\mathcal{M}}_{{\rm Dol}}^{{\rm sing}}\to \overline{\mathcal{M}}_{{\rm Hit}}^{{\rm sing}}$
is neither surjective nor injective.
$\overline{\Xi }^{{\rm sing}}:\overline{\mathcal{M}}_{{\rm Dol}}^{{\rm sing}}\to \overline{\mathcal{M}}_{{\rm Hit}}^{{\rm sing}}$
is neither surjective nor injective.
8.2 Discontinuity properties of the compactified Kobayashi–Hitchin map
In this subsection, we prove that the discontinuity of the compactified Kobayashi–Hitchin map (30) is fully determined by the discontinuity of the analytic Mochizuki map.
Let
![]() $(\mathcal{E}_{i},t_i\varphi _{i})$
be a sequence of Higgs bundles with real numbers
$(\mathcal{E}_{i},t_i\varphi _{i})$
be a sequence of Higgs bundles with real numbers
![]() $t_i\to +\infty$
,
$t_i\to +\infty$
,
![]() $\det (\varphi _i)=q_i$
,
$\det (\varphi _i)=q_i$
,
![]() $Z_i=q_i^{-1}(0)$
and
$Z_i=q_i^{-1}(0)$
and
![]() $\|q_i\|_{L^2}=1$
. We denote
$\|q_i\|_{L^2}=1$
. We denote
![]() $\xi _i=[(\mathcal{E}_i,t_i\varphi _i)]\in \mathcal{M}_{{\rm Dol}}$
. By the compactness of
$\xi _i=[(\mathcal{E}_i,t_i\varphi _i)]\in \mathcal{M}_{{\rm Dol}}$
. By the compactness of
![]() $\overline{\mathcal{M}}_{{\rm Dol}}$
, after passing to a subsequence we may assume there is
$\overline{\mathcal{M}}_{{\rm Dol}}$
, after passing to a subsequence we may assume there is
![]() $\xi _{\infty }\in \partial \overline{\mathcal{M}}_{{\rm Dol}}$
such that
$\xi _{\infty }\in \partial \overline{\mathcal{M}}_{{\rm Dol}}$
such that
![]() $\lim _{i\to \infty }\xi _i=\xi _{\infty }$
. Since
$\lim _{i\to \infty }\xi _i=\xi _{\infty }$
. Since
![]() $\partial \overline{\mathcal{M}}_{{\rm Dol}}\cong (\mathcal{M}_{{\rm Dol}}\setminus \mathcal{H}^{-1}(0))/\mathbb{C}^{\ast }$
, we can select a representative
$\partial \overline{\mathcal{M}}_{{\rm Dol}}\cong (\mathcal{M}_{{\rm Dol}}\setminus \mathcal{H}^{-1}(0))/\mathbb{C}^{\ast }$
, we can select a representative
![]() $(\mathcal{E}_{\infty },\varphi _{\infty })$
of
$(\mathcal{E}_{\infty },\varphi _{\infty })$
of
![]() $\xi _{\infty }$
. By Proposition 7.9, we have that
$\xi _{\infty }$
. By Proposition 7.9, we have that
![]() $(\mathcal{E}_i,\varphi _i)$
converges to
$(\mathcal{E}_i,\varphi _i)$
converges to
![]() $(\mathcal{E}_{\infty },\varphi _{\infty })$
in
$(\mathcal{E}_{\infty },\varphi _{\infty })$
in
![]() $\mathcal{M}_{{\rm Dol}}$
and that
$\mathcal{M}_{{\rm Dol}}$
and that
![]() $q_i$
converges to
$q_i$
converges to
![]() $q_{\infty }$
. We write
$q_{\infty }$
. We write
![]() $Z_{\infty }=q_{\infty }^{-1}(0).$
We note that for different choices of
$Z_{\infty }=q_{\infty }^{-1}(0).$
We note that for different choices of
![]() $t_i$
, as long as
$t_i$
, as long as
![]() $\lim _{i\to \infty }t_i=+\infty$
after passing to a subsequence, we always have
$\lim _{i\to \infty }t_i=+\infty$
after passing to a subsequence, we always have
![]() $\lim _{i\to \infty }\xi =\xi _{\infty }\in \overline{\mathcal{M}}_{{\rm Dol}}$
.
$\lim _{i\to \infty }\xi =\xi _{\infty }\in \overline{\mathcal{M}}_{{\rm Dol}}$
.
By Proposition 4.6,
![]() $\lim _{i\to \infty }\overline{\Xi }(\mathcal{E}_i,t_i\varphi _i)$
exists. The following result establishes the discontinuity of this map with respect to the analytic Mochizuki map
$\lim _{i\to \infty }\overline{\Xi }(\mathcal{E}_i,t_i\varphi _i)$
exists. The following result establishes the discontinuity of this map with respect to the analytic Mochizuki map
![]() $\Upsilon ^{{\rm Moc}}$
:
$\Upsilon ^{{\rm Moc}}$
:
Proposition 8.2.
Under the previous conventions, suppose that
![]() $q_i,q_{\infty }$
are irreducible. Consider
$q_i,q_{\infty }$
are irreducible. Consider
![]() $(\mathcal{E}_i,\varphi _i)\in \mathcal{M}_{q_i}$
; if
$(\mathcal{E}_i,\varphi _i)\in \mathcal{M}_{q_i}$
; if
![]() $\lim _{i\to \infty }\Upsilon ^{{\rm Moc}}(\mathcal{E}_i,\varphi _i)\neq \Upsilon ^{{\rm Moc}}(\mathcal{E}_{\infty },\varphi _{\infty }),$
then there exist constants
$\lim _{i\to \infty }\Upsilon ^{{\rm Moc}}(\mathcal{E}_i,\varphi _i)\neq \Upsilon ^{{\rm Moc}}(\mathcal{E}_{\infty },\varphi _{\infty }),$
then there exist constants
![]() $t_i$
such that for
$t_i$
such that for
![]() $\xi _i:=(\mathcal{E}_i,t_i\varphi _i)$
, we have
$\xi _i:=(\mathcal{E}_i,t_i\varphi _i)$
, we have
![]() $\lim _{i\to \infty }\overline{\Xi }(\xi _i)\neq \overline{\Xi }(\xi _{\infty })$
.
$\lim _{i\to \infty }\overline{\Xi }(\xi _i)\neq \overline{\Xi }(\xi _{\infty })$
.
Proof. Set
 \begin{align*} \overline{\Xi }(\mathcal{E}_i,t_i\varphi _i) & =\Xi (\mathcal{E}_i,t_i\varphi _i)=A_i+t_i\phi _i\;\\ \Upsilon ^{{\rm Moc}}(\mathcal{E}_i,\varphi _i) & =(A_i^{{\rm Lim}},\phi _i^{{\rm Lim}})\; and \\ \Upsilon ^{{\rm Moc}}(\mathcal{E}_{\infty },\varphi _{\infty }) & =(A_{\infty }^{{\rm Lim}},\phi _{\infty }^{{\rm Lim}}), \end{align*}
\begin{align*} \overline{\Xi }(\mathcal{E}_i,t_i\varphi _i) & =\Xi (\mathcal{E}_i,t_i\varphi _i)=A_i+t_i\phi _i\;\\ \Upsilon ^{{\rm Moc}}(\mathcal{E}_i,\varphi _i) & =(A_i^{{\rm Lim}},\phi _i^{{\rm Lim}})\; and \\ \Upsilon ^{{\rm Moc}}(\mathcal{E}_{\infty },\varphi _{\infty }) & =(A_{\infty }^{{\rm Lim}},\phi _{\infty }^{{\rm Lim}}), \end{align*}
with
![]() $t_i$
to be determined later and
$t_i$
to be determined later and
![]() $(A_i,\phi _i)$
depending on
$(A_i,\phi _i)$
depending on
![]() $t$
. Fixing a positive integer
$t$
. Fixing a positive integer
![]() $k$
, supposing
$k$
, supposing
![]() $\lim _{i\to \infty }\Upsilon ^{{\rm Moc}}(\mathcal{E}_i,\varphi _i)\neq \Upsilon ^{{\rm Moc}}(\mathcal{E}_{\infty },\varphi _{\infty }),$
and then passing to a subsequence, we could assume that there exist a compact set
$\lim _{i\to \infty }\Upsilon ^{{\rm Moc}}(\mathcal{E}_i,\varphi _i)\neq \Upsilon ^{{\rm Moc}}(\mathcal{E}_{\infty },\varphi _{\infty }),$
and then passing to a subsequence, we could assume that there exist a compact set
![]() $K\subset \Sigma \setminus Z_{\infty }$
and
$K\subset \Sigma \setminus Z_{\infty }$
and
![]() $\epsilon _0\gt 0$
such that
$\epsilon _0\gt 0$
such that
![]() $\|(A_i^{{\rm Lim}},\phi _i^{{\rm Lim}})-(A^{{\rm Lim}}_{\infty },\phi ^{{\rm Lim}}_{\infty })\|_{\mathcal{C}^k(K)}\geq \epsilon _0$
for
$\|(A_i^{{\rm Lim}},\phi _i^{{\rm Lim}})-(A^{{\rm Lim}}_{\infty },\phi ^{{\rm Lim}}_{\infty })\|_{\mathcal{C}^k(K)}\geq \epsilon _0$
for
![]() $i\geq i^{\prime}_0$
.
$i\geq i^{\prime}_0$
.
By Theorem 6.16, for the fixed compact set
![]() $K$
above and for each
$K$
above and for each
![]() $(\mathcal{E}_i,\varphi _i)$
, there exist
$(\mathcal{E}_i,\varphi _i)$
, there exist
![]() $t_i$
that are sufficiently large such that
$t_i$
that are sufficiently large such that
![]() $\|(A_i,\phi _i)-(A_i^{{\rm Lim}},\phi _i^{{\rm Lim}})\|_{\mathcal{C}^{k}(K)}\lt \frac 14\epsilon _0$
. Moreover, by Proposition 4.6, there is a limiting configuration
$\|(A_i,\phi _i)-(A_i^{{\rm Lim}},\phi _i^{{\rm Lim}})\|_{\mathcal{C}^{k}(K)}\lt \frac 14\epsilon _0$
. Moreover, by Proposition 4.6, there is a limiting configuration
![]() $(A_{\infty },\phi _{\infty }):=\lim _{i\to \infty }(A_i,\phi _i)$
defined over
$(A_{\infty },\phi _{\infty }):=\lim _{i\to \infty }(A_i,\phi _i)$
defined over
![]() $\Sigma \setminus Z_{\infty }$
such that over
$\Sigma \setminus Z_{\infty }$
such that over
![]() $K$
and for
$K$
and for
![]() $i\geq i^{\prime\prime}_0$
, we have
$i\geq i^{\prime\prime}_0$
, we have
For
![]() $i\geq \max \{i^{\prime}_0,i^{\prime\prime}_0\}$
, we compute
$i\geq \max \{i^{\prime}_0,i^{\prime\prime}_0\}$
, we compute
 \begin{align*} & \|(A_{\infty },\phi _{\infty })-(A_{\infty }^{{\rm Lim}},\phi _{\infty }^{{\rm Lim}})\|_{\mathcal{C}^k(K)} \geq \|(A_i^{{\rm Lim}},\phi _i^{{\rm Lim}})-(A_{\infty }^{{\rm Lim}},\phi _{\infty }^{{\rm Lim}})\|_{\mathcal{C}^k(K)} \\ & \quad -\|(A_{\infty },\phi _{\infty })-(A_i,\phi _i)\|_{\mathcal{C}^{k}(K)}-\|(A_i,\phi _i)-(A_i^{{\rm Lim}},\phi _i^{{\rm Lim}})\|_{\mathcal{C}^{k}(K)}\\ & \geq \frac 12\epsilon _0. \end{align*}
\begin{align*} & \|(A_{\infty },\phi _{\infty })-(A_{\infty }^{{\rm Lim}},\phi _{\infty }^{{\rm Lim}})\|_{\mathcal{C}^k(K)} \geq \|(A_i^{{\rm Lim}},\phi _i^{{\rm Lim}})-(A_{\infty }^{{\rm Lim}},\phi _{\infty }^{{\rm Lim}})\|_{\mathcal{C}^k(K)} \\ & \quad -\|(A_{\infty },\phi _{\infty })-(A_i,\phi _i)\|_{\mathcal{C}^{k}(K)}-\|(A_i,\phi _i)-(A_i^{{\rm Lim}},\phi _i^{{\rm Lim}})\|_{\mathcal{C}^{k}(K)}\\ & \geq \frac 12\epsilon _0. \end{align*}
This proves the proposition.
8.2.1 Continuity along rays
We now investigate the behavior of the compactified Kobayashi–Hitchin map when it is restricted to a singular fibre. Specifically, fix
![]() $0\neq q\in H^0(K^2)$
, and denote by
$0\neq q\in H^0(K^2)$
, and denote by
![]() $[q]$
the
$[q]$
the
![]() $\mathbb{C}^\ast$
-orbit of
$\mathbb{C}^\ast$
-orbit of
![]() $q\times{1}$
in the compactified Hitchin base
$q\times{1}$
in the compactified Hitchin base
![]() $\overline{\mathcal{B}}$
. Define
$\overline{\mathcal{B}}$
. Define
![]() ${\overline{\mathcal{M}}_{{\rm Dol},[q]}}:=\overline{\mathcal{H}}^{-1}_{{\rm Dol}}([q])$
and
${\overline{\mathcal{M}}_{{\rm Dol},[q]}}:=\overline{\mathcal{H}}^{-1}_{{\rm Dol}}([q])$
and
![]() ${\overline{\mathcal{M}}_{{\rm Hit},[q]}}:=\overline{\mathcal{H}}^{-1}_{{\rm Hit}}([q])$
. Then the restriction of
${\overline{\mathcal{M}}_{{\rm Hit},[q]}}:=\overline{\mathcal{H}}^{-1}_{{\rm Hit}}([q])$
. Then the restriction of
![]() $\overline{\Xi }$
on
$\overline{\Xi }$
on
![]() $\overline{\mathcal{M}}_{{\rm Dol},[q]}$
defines a map
$\overline{\mathcal{M}}_{{\rm Dol},[q]}$
defines a map
![]() $\overline{\Xi }_{[q]}:{\overline{\mathcal{M}}_{{\rm Dol},[q]}}\to{\overline{\mathcal{M}}_{{\rm Hit},[q]}}$
.
$\overline{\Xi }_{[q]}:{\overline{\mathcal{M}}_{{\rm Dol},[q]}}\to{\overline{\mathcal{M}}_{{\rm Hit},[q]}}$
.
Theorem 8.3.
Let
![]() $q$
be an irreducible quadratic differential.
$q$
be an irreducible quadratic differential.
-
(i) The boundary map
 $\partial \overline{\Xi }_{[q]}|_{\overline{\mathcal{M}}_{{\rm Dol},[q]}}$
is continuous if
$\partial \overline{\Xi }_{[q]}|_{\overline{\mathcal{M}}_{{\rm Dol},[q]}}$
is continuous if
 $q$
has only zeros of odd order and is discontinuous if
$q$
has only zeros of odd order and is discontinuous if
 $q$
has at least one zero of even order.
$q$
has at least one zero of even order.
-
(ii) If
 $q$
has at least one zero of even order, then for each
$q$
has at least one zero of even order, then for each
 $\sigma$
-divisor
$\sigma$
-divisor
 $D\neq 0$
, there exists an even integer
$D\neq 0$
, there exists an even integer
 $n_D\geq 1$
so that for any Higgs bundle
$n_D\geq 1$
so that for any Higgs bundle
 $(\mathcal{F},\psi )\in \mathcal{M}_{q,D}$
, there exist
$(\mathcal{F},\psi )\in \mathcal{M}_{q,D}$
, there exist
 $2n_D$
sequences of Higgs bundles
$2n_D$
sequences of Higgs bundles
 $(\mathcal{E}_i^k,\varphi _i^k)$
,
$(\mathcal{E}_i^k,\varphi _i^k)$
,
 $k=1,\ldots, 2n_D$
such that
$k=1,\ldots, 2n_D$
such that
-
*
 $\lim _{i\to \infty }(\mathcal{E}_i^k,\varphi _i^k)=(\mathcal{F},\psi )$
for
$\lim _{i\to \infty }(\mathcal{E}_i^k,\varphi _i^k)=(\mathcal{F},\psi )$
for
 $k=1,\ldots,2n_D$
;
$k=1,\ldots,2n_D$
; -
* and if we write
 \begin{align*}\eta ^k:=\lim _{i\to \infty }\partial \overline {\Xi }_{[q]}(\mathcal {E}_i^k,t_i\varphi _i^k)\quad, then \quad \xi :=\lim _{i\to \infty }\partial \overline {\Xi }_{[q]}(\mathcal {F},t_i\psi )\;\end{align*}
\begin{align*}\eta ^k:=\lim _{i\to \infty }\partial \overline {\Xi }_{[q]}(\mathcal {E}_i^k,t_i\varphi _i^k)\quad, then \quad \xi :=\lim _{i\to \infty }\partial \overline {\Xi }_{[q]}(\mathcal {F},t_i\psi )\;\end{align*}
-
-
• if
 $(\mathcal{F},\psi )$
doesn’t lie in the real locus, then
$(\mathcal{F},\psi )$
doesn’t lie in the real locus, then
 $\xi,\eta^1,\ldots,\eta ^{2n_D}$
are
$\xi,\eta^1,\ldots,\eta ^{2n_D}$
are
 $2n_D+1$
different limiting configurations,
$2n_D+1$
different limiting configurations,
-
• if
 $(\mathcal{F},\psi )$
lies in the real locus, then
$(\mathcal{F},\psi )$
lies in the real locus, then
 $\eta ^i\cong \eta ^{n_D+i}$
for
$\eta ^i\cong \eta ^{n_D+i}$
for
 $i=1,\cdots,n$
and we obtain
$i=1,\cdots,n$
and we obtain
 $n_D+1$
different limiting configurations.
$n_D+1$
different limiting configurations.
-
* for each
 $k$
, there exists constants
$k$
, there exists constants
 $t_i\to +\infty$
such that
$t_i\to +\infty$
such that
 $\lim _{i\to \infty }\overline{\Xi }_{[q]}(\mathcal{E}_i^k,t_i\varphi _i^k)\neq \overline{\Xi }_{[q]}(\mathcal{F},\psi )$
.
$\lim _{i\to \infty }\overline{\Xi }_{[q]}(\mathcal{E}_i^k,t_i\varphi _i^k)\neq \overline{\Xi }_{[q]}(\mathcal{F},\psi )$
.
8.2.2 Varying fibre
With the conventions above, suppose that
![]() $(\mathcal{E}_i,\varphi _i)$
converges to
$(\mathcal{E}_i,\varphi _i)$
converges to
![]() $(\mathcal{E}_{\infty },\varphi _{\infty })$
, with
$(\mathcal{E}_{\infty },\varphi _{\infty })$
, with
![]() $q_{\infty }$
having only simple zeros, and that
$q_{\infty }$
having only simple zeros, and that
![]() $\xi _i=(\mathcal{E}_i,t_i\varphi _i)$
converges to
$\xi _i=(\mathcal{E}_i,t_i\varphi _i)$
converges to
![]() $\xi _\infty$
on
$\xi _\infty$
on
![]() $\overline{\mathcal{M}}_{{\rm Dol}}$
. Since the condition of having only simple zeros is open, the
$\overline{\mathcal{M}}_{{\rm Dol}}$
. Since the condition of having only simple zeros is open, the
![]() $q_i$
’s also have simple zeros when
$q_i$
’s also have simple zeros when
![]() $i$
is sufficiently large.
$i$
is sufficiently large.
Proposition 8.4.
Suppose
![]() $q_{\infty }$
has only simple zeros. Then
$q_{\infty }$
has only simple zeros. Then
![]() $\displaystyle \lim _{i\to \infty }\overline{\Xi }(\xi _i)=\overline{\Xi }(\xi _\infty )$
. In particular, the map
$\displaystyle \lim _{i\to \infty }\overline{\Xi }(\xi _i)=\overline{\Xi }(\xi _\infty )$
. In particular, the map
![]() $\overline{\Xi }^{{\rm reg}}:\overline{\mathcal{M}}_{{\rm Dol}}^{{\rm reg}}\to \overline{\mathcal{M}}_{{\rm Hit}}^{{\rm reg}}$
is continuous.
$\overline{\Xi }^{{\rm reg}}:\overline{\mathcal{M}}_{{\rm Dol}}^{{\rm reg}}\to \overline{\mathcal{M}}_{{\rm Hit}}^{{\rm reg}}$
is continuous.
Proof.
Let
![]() $S_i$
denote the spectral curve of
$S_i$
denote the spectral curve of
![]() $(\mathcal{E}_i,\varphi _i)$
, with branching locus
$(\mathcal{E}_i,\varphi _i)$
, with branching locus
![]() $Z_i$
. Also, let
$Z_i$
. Also, let
![]() $L_i:=\chi _{{\rm BNR}}^{-1}(\mathcal{E}_i,\varphi _i)$
be the eigenline bundles. By the construction in Section 6, we have
$L_i:=\chi _{{\rm BNR}}^{-1}(\mathcal{E}_i,\varphi _i)$
be the eigenline bundles. By the construction in Section 6, we have
![]() $\Upsilon ^{{\rm Moc}}(\xi _i)=\mathcal{F}_{\ast }(L_i,\chi _i)$
, where
$\Upsilon ^{{\rm Moc}}(\xi _i)=\mathcal{F}_{\ast }(L_i,\chi _i)$
, where
![]() $\chi _i=-\frac 12\chi _{Z_i}$
. Our assumption implies that
$\chi _i=-\frac 12\chi _{Z_i}$
. Our assumption implies that
![]() $\mathcal{F}_{\ast }(L_i,\chi _i)$
converges to
$\mathcal{F}_{\ast }(L_i,\chi _i)$
converges to
![]() $\mathcal{F}_{\ast }(L_{\infty },\chi _{\infty })$
in the sense of Definition 3.2. Thus, by Theorem 3.3, we obtain the convergence of the limiting configurations:
$\mathcal{F}_{\ast }(L_{\infty },\chi _{\infty })$
in the sense of Definition 3.2. Thus, by Theorem 3.3, we obtain the convergence of the limiting configurations:
![]() $\lim _{i\to \infty }\Upsilon ^{{\rm Moc}}(\xi _i)=\Upsilon ^{{\rm Moc}}(\xi _{\infty })$
. The claim follows from Proposition 8.2.
$\lim _{i\to \infty }\Upsilon ^{{\rm Moc}}(\xi _i)=\Upsilon ^{{\rm Moc}}(\xi _{\infty })$
. The claim follows from Proposition 8.2.
Theorem 8.5.
The map
![]() $\overline{\Xi }^{{\rm reg}}:\overline{\mathcal{M}}_{{\rm Dol}}^{{\rm reg}}\to \overline{\mathcal{M}}_{{\rm Hit}}^{{\rm reg}}$
is a homeomorphism.
$\overline{\Xi }^{{\rm reg}}:\overline{\mathcal{M}}_{{\rm Dol}}^{{\rm reg}}\to \overline{\mathcal{M}}_{{\rm Hit}}^{{\rm reg}}$
is a homeomorphism.
Proof.
By Theorem 4.9,
![]() $\overline{\Xi }^{{\rm reg}}$
is a bijection. Moreover, by Proposition 8.4,
$\overline{\Xi }^{{\rm reg}}$
is a bijection. Moreover, by Proposition 8.4,
![]() $\overline{\Xi }^{{\rm reg}}$
is continuous. Finally, that
$\overline{\Xi }^{{\rm reg}}$
is continuous. Finally, that
![]() $(\overline{\Xi }^{{\rm reg}})^{-1}$
is continuous follows directly from the construction in [Reference Mazzeo, Swoboda, Weiss and WittMSWW19].
$(\overline{\Xi }^{{\rm reg}})^{-1}$
is continuous follows directly from the construction in [Reference Mazzeo, Swoboda, Weiss and WittMSWW19].
Appendix A. Classification of rank 1 torsion-free modules for
 $A_n$
singularities
$A_n$
singularities
In this appendix, we review the classification result for rank 1 torsion-free modules at
![]() $A_n$
singularities, as given in [Reference Greuel and KnörrerGK85]. We compute the integer invariants defined in Section 5.3.
$A_n$
singularities, as given in [Reference Greuel and KnörrerGK85]. We compute the integer invariants defined in Section 5.3.
Let
![]() $S$
be the spectral curve of an
$S$
be the spectral curve of an
![]() ${\rm SL}(2,\mathbb{C})$
Higgs bundle, and let
${\rm SL}(2,\mathbb{C})$
Higgs bundle, and let
![]() $x$
be a singular point with local defining equation given by
$x$
be a singular point with local defining equation given by
![]() $r^2-s^{n+1}=0$
; this is an
$r^2-s^{n+1}=0$
; this is an
![]() $A_n$
singularity. Let
$A_n$
singularity. Let
![]() $p:\widetilde{S}\to S$
be the normalisation, where
$p:\widetilde{S}\to S$
be the normalisation, where
![]() $p^{-1}(x)=\{\tilde{x}_+,\tilde{x}_-\}$
if
$p^{-1}(x)=\{\tilde{x}_+,\tilde{x}_-\}$
if
![]() $n$
is odd and
$n$
is odd and
![]() $p^{-1}(x)={\tilde{x}}$
if
$p^{-1}(x)={\tilde{x}}$
if
![]() $n$
is even. We use
$n$
is even. We use
![]() $R$
to denote the completion of the local ring
$R$
to denote the completion of the local ring
![]() $\mathcal{O}_x$
,
$\mathcal{O}_x$
,
![]() $K$
to denote its field of fractions and
$K$
to denote its field of fractions and
![]() $\widetilde{R}$
to denote its normalization.
$\widetilde{R}$
to denote its normalization.
A.1
 $\boldsymbol{A}_{2\boldsymbol{n}}$
singularity
$\boldsymbol{A}_{2\boldsymbol{n}}$
singularity
The local equation is
![]() $r^2-s^{2n+1}=0$
. The normalization induces a map between coordinate rings, and we can write
$r^2-s^{2n+1}=0$
. The normalization induces a map between coordinate rings, and we can write
where
![]() $\widetilde{R}=\mathbb{C}[[t]]$
and
$\widetilde{R}=\mathbb{C}[[t]]$
and
![]() $R=\mathbb{C}[[t^2,t^{2n+1}]]\subset \widetilde{R}$
. According to [Reference Greuel and KnörrerGK85, Anh. (1.1)], any rank 1 torsion-free
$R=\mathbb{C}[[t^2,t^{2n+1}]]\subset \widetilde{R}$
. According to [Reference Greuel and KnörrerGK85, Anh. (1.1)], any rank 1 torsion-free
![]() $R$
-module can be written as
$R$
-module can be written as
Here,
![]() $M_k$
is a fractional ideal that satisfies
$M_k$
is a fractional ideal that satisfies
![]() $R\subset M_k\subset \widetilde{R}$
, with
$R\subset M_k\subset \widetilde{R}$
, with
![]() $M_1=\widetilde{R}$
and
$M_1=\widetilde{R}$
and
![]() $M_{2n+1}=R$
. We may express any
$M_{2n+1}=R$
. We may express any
![]() $f \in M_k$
as
$f \in M_k$
as
![]() $f = \sum _{i=0}^{{k-1 \over 2}} f_{2i}t^{2i}+\sum _{i\geq k}f_it^i$
, where
$f = \sum _{i=0}^{{k-1 \over 2}} f_{2i}t^{2i}+\sum _{i\geq k}f_it^i$
, where
![]() $f_i\in \mathbb{C}$
.
$f_i\in \mathbb{C}$
.
We are interested in the integers
![]() $\ell _x := \dim _{\mathbb{C}}(M_k/R)$
,
$\ell _x := \dim _{\mathbb{C}}(M_k/R)$
,
![]() $a_{\tilde{x}} := \dim _{\mathbb{C}}(\widetilde{R}/C(M_k))$
and
$a_{\tilde{x}} := \dim _{\mathbb{C}}(\widetilde{R}/C(M_k))$
and
![]() $b_x=\dim _{\mathbb{C}}({T}(M_k\otimes _R \widetilde{R}))$
(where
$b_x=\dim _{\mathbb{C}}({T}(M_k\otimes _R \widetilde{R}))$
(where
![]() $T$
denotes the torsion-free submodule). Thus, as a
$T$
denotes the torsion-free submodule). Thus, as a
![]() $\mathbb{C}$
-vector space,
$\mathbb{C}$
-vector space,
![]() $M_k/R$
is generated by
$M_k/R$
is generated by
![]() $t^k, t^{k+2}, \ldots, t^{2n-1}$
, implying that
$t^k, t^{k+2}, \ldots, t^{2n-1}$
, implying that
![]() $\ell _x={2n+1-k \over 2}$
.
$\ell _x={2n+1-k \over 2}$
.
The conductor of
![]() $M_k$
is given by
$M_k$
is given by
![]() $C(M_k) = \{u\in K\mid u\cdot \widetilde{R}\subset M_k\}$
. By the expression of
$C(M_k) = \{u\in K\mid u\cdot \widetilde{R}\subset M_k\}$
. By the expression of
![]() $M_k$
and a straightforward computation, we have
$M_k$
and a straightforward computation, we have
![]() $C(M_k) = (t^{k-1})$
, where
$C(M_k) = (t^{k-1})$
, where
![]() $(t^{k-1})$
is the ideal in
$(t^{k-1})$
is the ideal in
![]() $\widetilde{R}$
generated by
$\widetilde{R}$
generated by
![]() $t^{k-1}$
. Thus,
$t^{k-1}$
. Thus,
![]() $1,t,\ldots,t^{k-2}$
will form a basis for
$1,t,\ldots,t^{k-2}$
will form a basis for
![]() $\widetilde{R}/C(M_k)$
, and we have
$\widetilde{R}/C(M_k)$
, and we have
![]() $a_{\tilde{x}}=k-1$
. Therefore, we have
$a_{\tilde{x}}=k-1$
. Therefore, we have
![]() $a_{\tilde{x}}=2n-2\ell _x$
.
$a_{\tilde{x}}=2n-2\ell _x$
.
For
![]() $i=0, 1,\ldots,{2n-1-k \over 2}$
, we define
$i=0, 1,\ldots,{2n-1-k \over 2}$
, we define
![]() $s_i=t^{k+2i}\otimes _R 1-1\otimes t^{k+2i}\in M_k\otimes _R\widetilde{R}$
. As
$s_i=t^{k+2i}\otimes _R 1-1\otimes t^{k+2i}\in M_k\otimes _R\widetilde{R}$
. As
![]() $k$
is odd,
$k$
is odd,
![]() $t^{2n+1-k-2i}\in R$
and
$t^{2n+1-k-2i}\in R$
and
![]() $t^{2n+1-k-2i}s_i=t^{2n+1}\otimes _R 1-1\otimes _R t^{2n+1}=0$
, where the last equality occurs because
$t^{2n+1-k-2i}s_i=t^{2n+1}\otimes _R 1-1\otimes _R t^{2n+1}=0$
, where the last equality occurs because
![]() $t^{2n+1}\in R$
. Moreover,
$t^{2n+1}\in R$
. Moreover,
![]() $\{s_1,\ldots, s_{{2n-1-k \over 2}}\}$
form a basis of
$\{s_1,\ldots, s_{{2n-1-k \over 2}}\}$
form a basis of
![]() ${T}(M_k\otimes _R\widetilde{R})$
; thus
${T}(M_k\otimes _R\widetilde{R})$
; thus
![]() $b_x={2n+1-k \over 2}=\ell _x$
.
$b_x={2n+1-k \over 2}=\ell _x$
.
A.2
 $\textit{\textbf{A}}_{\textbf{2}\textit{\textbf{n}}-\textbf{1}}$
singularity
$\textit{\textbf{A}}_{\textbf{2}\textit{\textbf{n}}-\textbf{1}}$
singularity
The local equation is
![]() $r^2-s^{2n}=0$
. The normalisation induces a map between the coordinate rings:
$r^2-s^{2n}=0$
. The normalisation induces a map between the coordinate rings:
where
![]() $\widetilde{R}=\mathbb{C}[[t]]\oplus \mathbb{C}[[t]]$
and
$\widetilde{R}=\mathbb{C}[[t]]\oplus \mathbb{C}[[t]]$
and
![]() $R=\mathbb{C}[[(t,t),(t^n,-t^n)]]\cong \mathbb{C}[[(t,t),(t^n,0)]]$
. By [Reference Greuel and KnörrerGK85, Anh. (2.1)], any rank 1 torsion-free
$R=\mathbb{C}[[(t,t),(t^n,-t^n)]]\cong \mathbb{C}[[(t,t),(t^n,0)]]$
. By [Reference Greuel and KnörrerGK85, Anh. (2.1)], any rank 1 torsion-free
![]() $R$
-module can be written as:
$R$
-module can be written as:
Then
![]() $M_k$
is also a fractional ideal, with
$M_k$
is also a fractional ideal, with
![]() $R\subset M_k\subset \widetilde{R}$
. Moreover,
$R\subset M_k\subset \widetilde{R}$
. Moreover,
![]() $M_n=R$
, and
$M_n=R$
, and
![]() $M_0=\widetilde{R}$
.
$M_0=\widetilde{R}$
.
As
![]() $p^{-1}(x)=\{\tilde{x}_+,\tilde{x}_-\}$
,
$p^{-1}(x)=\{\tilde{x}_+,\tilde{x}_-\}$
,
![]() $\widetilde{R}$
contains two maximal ideals,
$\widetilde{R}$
contains two maximal ideals,
![]() $\mathfrak{m}_+=((t,1))$
,
$\mathfrak{m}_+=((t,1))$
,
![]() $\mathfrak{m}_-=((1,t))$
. For
$\mathfrak{m}_-=((1,t))$
. For
![]() $f\in M_k$
, we can express
$f\in M_k$
, we can express
![]() $f$
as:
$f$
as:
 \begin{align*} f=\sum _{i=0}^{k-1}f_{ii}(t^i,t^i)+\sum _{l\geq 0}f_{l0}(t^{k+l},0)+f_{0l}(0,t^{k+l}), \end{align*}
\begin{align*} f=\sum _{i=0}^{k-1}f_{ii}(t^i,t^i)+\sum _{l\geq 0}f_{l0}(t^{k+l},0)+f_{0l}(0,t^{k+l}), \end{align*}
where
![]() $f_{ij}\in \mathbb{C}$
. Therefore,
$f_{ij}\in \mathbb{C}$
. Therefore,
![]() $\ell _x=\dim _{\mathbb{C}}(M_k/R)=n-k$
. Moreover, using this expression, we can compute the conductor
$\ell _x=\dim _{\mathbb{C}}(M_k/R)=n-k$
. Moreover, using this expression, we can compute the conductor
![]() $C(M_k)=((t^k,1))\cdot ((1,t^k))$
, which implies
$C(M_k)=((t^k,1))\cdot ((1,t^k))$
, which implies
![]() $a_{\tilde{x}_{\pm }}=k$
. Similarly, for
$a_{\tilde{x}_{\pm }}=k$
. Similarly, for
![]() $i=k,\ldots,n-1$
, we define
$i=k,\ldots,n-1$
, we define
![]() $s_i=(t^i,0)\otimes _R(1,1)-(1,1)\otimes _R (t^i,0)$
; then
$s_i=(t^i,0)\otimes _R(1,1)-(1,1)\otimes _R (t^i,0)$
; then
![]() $(t,t)^{n-i}\cdot s_i=0$
, and
$(t,t)^{n-i}\cdot s_i=0$
, and
![]() $\{s_k,\ldots, s_{n-1}\}$
will be a basis for
$\{s_k,\ldots, s_{n-1}\}$
will be a basis for
![]() ${T}(M_k\otimes _R \widetilde{R})$
and
${T}(M_k\otimes _R \widetilde{R})$
and
![]() $b_x=\ell _x$
.
$b_x=\ell _x$
.
In summary, we have the following:
Proposition 9.2.1. For the integers defined above, we have:
-
(i) for the
 $A_{2n}$
singularity, we have
$A_{2n}$
singularity, we have
 $a_{\tilde{x}}=2n-2\ell _x$
and
$a_{\tilde{x}}=2n-2\ell _x$
and
 $b_x=\ell _x$
;
$b_x=\ell _x$
; -
(ii) for the
 $A_{2n-1}$
singularity, we have
$A_{2n-1}$
singularity, we have
 $a_{\tilde{x}_{\pm }}=n-\ell _x$
and
$a_{\tilde{x}_{\pm }}=n-\ell _x$
and
 $b_x=\ell _x$
.
$b_x=\ell _x$
.
Acknowledgements
We extend our sincere gratitude to Takurō Mochizuki for his valuable insights and stimulating discussions during the BIRS conference in 2021. The authors would also like to thank the anonymous referee for their meticulous review of the manuscript, as well as for their valuable comments and recommendations. Additionally, the authors thank the following for their interest and helpful comments: Mark de Cataldo, Ron Donagi, Simon Donaldson, Laura Fredrickson, Johannes Horn, Laura Schaposnik, Shizhang Li, Jie Liu, Tony Pantev, Szilárd Szabó, Thomas Walpuski, and Daxin Xu.
Conflicts of Interest
None.
Financial Support
S. H. is supported by NSFC grant No.12288201 and National Key R&D Program No.2023YFA1010500. R. W.’s research is supported by NSF grant DMS-2204346, and he thanks the Max Planck Institute for Mathematics in Bonn for its hospitality and financial support. The authors also gratefully acknowledge the support of SLMath under NSF grant DMS-1928930 during the program ‘Analytic and Geometric Aspects of Gauge Theory’, Fall 2022.
Journal Information
Moduli is published as a joint venture of the Foundation Compositio Mathematica and the London Mathematical Society. As not-for-profit organisations, the Foundation and Society reinvest
![]() $100\%$
of any surplus generated from their publications back into mathematics through their charitable activities.
$100\%$
of any surplus generated from their publications back into mathematics through their charitable activities.