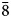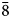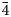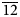Introduction
To confirm that the revised chemical formula for fettelite from Chañarcillo, Chile, [Ag6As2S7][Ag10HgAs2S8], proposed by Bindi et al. (Reference Bindi, Keutsch, Francis and Menchetti2009) is valid for all the fettelite samples, and to elucidate the role of the cation substitution at the linearly-coordinated Hg site, Bindi et al. (Reference Bindi, Downs, Spry, Pinch and Menchetti2012) reported a structural and chemical characterisation of two samples of fettelite from the type locality (Glasberg quarry, Nieder-Beerbach, Odenwald, south-western Germany). One of these samples turned out to be a possible new Fe-rich end-member. However, Bindi et al. (Reference Bindi, Downs, Spry, Pinch and Menchetti2012) obtained a chemical composition significantly different from ideal [i.e. ΣS = 15 atoms per formula unit, Σ(As+Sb) = 4 apfu, Ag = 16 apfu] owing to the strong sensitivity of these samples to the electron beam that made it very difficult to attain good and reliable microprobe data. Recently, with new equipment and standards, the problem was solved, and good chemical data were obtained. This allowed us to go ahead with the submission of a new mineral proposal. The mineral and name was approved by the Commission on New Minerals, Nomenclature and Classification of the International Mineralogical Association (IMA2021–094, Bindi and Downs, Reference Bindi and Downs2022) as ferrofettelite (symbol Fftt). The name indicates that the mineral is the Fe-dominant analogue of fettelite. Holotype material is deposited in the collections of the University of Arizona Gem and Mineral Museum, Tucson, Arizona, USA, catalogue number 22716.
Occurrence, physical and optical properties
The sample containing ferrofettelite was not found in situ, but originates from a sample (Fig. 1), which belonged to the William W. Pinch collection, reported to come from the Glasberg quarry, Nieder-Beerbach, Odenwald, south-western Germany (the type locality of fettelite; Wang and Paniagua, Reference Wang and Paniagua1996). Associated minerals include proustite and xanthoconite, on arsenolite, calcite and prehnite. We note that the association of fettelite with arsenolite was not reported by Wang and Paniagua (Reference Wang and Paniagua1996). As reported by Bindi et al. (Reference Bindi, Downs, Spry, Pinch and Menchetti2012), ferrofettelite, up to 250 μm in size, shows a grey reddish streak; it is opaque in transmitted light and exhibits a metallic lustre. No cleavage is observed, and the fracture is uneven. The calculated density (for Z = 8) from the empirical formula and single-crystal X-ray data is 5.74 g/cm3. Micro-indentation measurements carried out with a VHN load of 20 g give a mean value of 122 kg/mm2 (range: 111–131). A REE-super-magnet was placed in close proximity to a 200 μm fragment of ferrofettelite to explore potential paramagnetic susceptibility, but no effect was observed.

Fig. 1. Macroscopic image of the rock sample containing ferrofettelite (dark red). Scale bar and sample number are indicated.
In plane-polarised incident light, ferrofettelite is greyish white in colour, with moderate bireflectance (from white to brownish grey). Under crossed polars, it shows weak anisotropism with relatively strong red internal reflections. Reflectance measurements were performed in air by means of a MPM-200 Zeiss microphotometer equipped with a MSP-20 system processor on a Zeiss Axioplan ore microscope. The filament temperature was ~3350 K. An interference filter was adjusted to four wavelengths for measurement (471.1, 548.3, 586.6 and 652.3 nm). Readings were taken for the specimen and standard (SiC) at the same focus conditions. The diameter of the circular area that was measured was 0.1 mm. Reflectance percentages for R min and R max are 28.2, 29.4 (471.1 nm); 25.0, 26.3 (548.3 nm); 22.9, 23.5 (586.6 nm); and 20.9, 21.2 (652.3 nm).
Chemical composition
The chemical composition was determined using wavelength dispersive analysis (WDS) by means of a JEOL 8200 electron microprobe. Concentrations of major and minor elements were determined at an accelerating voltage of 15 kV and a beam current of 15 nA, with 20 s counting time (spot size 1 μm). For the WDS analyses the following lines were used: SKα, FeKα, CuKα, AsLα, AgLα, SbLβ, PbMα and HgLα. The standards employed were: pure metals for Cu and Ag, galena for Pb, pyrite for Fe and S, cinnabar for Hg, synthetic Sb2S3 for Sb and synthetic As2S3 for As. The ferrofettelite fragment was homogeneous within analytical error (N = 4).
It is noted that Bindi et al. (Reference Bindi, Downs, Spry, Pinch and Menchetti2012) previously reported a chemical analysis of ferrofettelite from the same specimen. They obtained a chemical composition significantly different from ideal, i.e. Ag16.45(Fe0.89Hg0.37Cu0.01)Σ1.27(As4.03Sb0.04)Σ4.07S14.21. These authors discussed the strong sensitivity of these samples to the electron beam, which caused Hg to vaporise out of the sample (they observed a gradual reduction of Hg with time and significant damage to the sample surface). This made it very difficult to obtain good and reliable microprobe data. Here, with new equipment (JEOL-JXA8600 vs. JEOL-JXA8320) and standards (same kind of materials but newly prepared with vibro-polishing), the problem was solved, and we were able to obtain very good chemical data and in agreement with the chemical formula obtained from the structure refinement (Bindi et al., Reference Bindi, Downs, Spry, Pinch and Menchetti2012). The results of the analyses are given in Table 1.
Table 1. Analytical data (in wt.%) for ferrofettelite.

S.D. = standard deviation
The empirical formula (based on 36 apfu) can be written as Ag16.04(Fe0.55Hg0.40Cu0.02)Σ0.97(As3.94Sb0.03)Σ3.97S15.02. The simplified formula is Ag16(Fe,Hg,Cu)(As,Sb)4S15. The ideal formula, taking into account the structural results (see below and Bindi et al., Reference Bindi, Downs, Spry, Pinch and Menchetti2012) is, [Ag6As2S7][Ag10FeAs2S8], which requires Ag 67.35, Fe 2.18, As 11.70, S 18.77, total 100 wt.%.
X-ray crystallography
The crystal structure refinement of ferrofettelite has been described in detail by Bindi et al. (Reference Bindi, Downs, Spry, Pinch and Menchetti2012) where the mineral was labelled R100124. At room temperature ferrofettelite is monoclinic (pseudo-hexagonal), space group C2, with a = 26.011(2), b = 15.048(1), c = 15.513(1) Å, β = 90.40(1)°, V = 6071.9(7) Å3 and Z = 8 [R = 0.0314 for 8136 reflections with I > 2σ(I)]. The crystallographic information file has been deposited with the Principal Editor of Mineralogical Magazine and is available as Supplementary material (see below).
Powder X-ray diffraction data (Table 2) were obtained with an Oxford Diffraction Xcalibur PX Ultra diffractometer fitted with a 165 mm diagonal Onyx CCD detector and using copper radiation (CuKα, λ = 1.54138 Å). The working conditions were 50 kV, 50 mA and 3 hours of exposure; the detector-to-sample distance was 7 cm. The program Crysalis RED was used to convert the observed diffraction rings to a conventional powder diffraction pattern. Least squares refinement gave the following values: a = 26.000(2), b = 15.067(2), c = 15.512(1) Å, β = 90.29(1)° and V = 6076.6(8) Å3.
Table 2. Observed and calculated powder X-ray diffraction data (d in Å) for ferrofettelite.

1 = observed diffraction pattern; 2 = calculated diffraction pattern obtained with the ferrofettelite structural model reported by Bindi et al. (Reference Bindi, Downs, Spry, Pinch and Menchetti2012) (only reflections with I rel ≥ 4 are listed). The strongest observed reflections are given in bold.
To compare the high-temperature behaviour of ferrofettelite with that of the Chilean fettelite (Bindi and Menchetti, Reference Bindi and Menchetti2011) the unit-cell values were carefully measured by means of an Oxford Diffraction Xcalibur 3 single-crystal diffractometer (enhanced X-ray source, X-ray radiation MoKα, λ = 0.71073 Å) fitted with a Sapphire 2 CCD detector. Moreover, in expectation of a possible phase transition towards a high-conducting form as for fettelite (Bindi and Menchetti, Reference Bindi and Menchetti2011), we monitored the intensities of some selected hkl reflections, i.e. 151, 352, 17$\bar{3}$![]() , 736, 442 and 441, together with their equivalent reflections (Fig. 2). We chose four hkl reflections with h and k = 2n+1 to see if the a and b parameters became halved with the increase of temperature (see Bindi et al., Reference Bindi, Keutsch, Francis and Menchetti2009), and two hkl reflections with h and k = 2n (always present) as standard. Subsequently, the temperature was raised to 310 K with a heating rate of 5 K/h, and the same data set was collected. The same procedure was then repeated at 320, 335, 350, 365, 380, 395 and 410 K (Fig. 2). The high (up to 410 K) temperatures were achieved by means of an Oxford cryostream cooler. Unlike what was observed for fettelite, the intensities of the selected reflections with h and k = 2n + 1 (i.e. 151, 352, 17$\bar{3}$
, 736, 442 and 441, together with their equivalent reflections (Fig. 2). We chose four hkl reflections with h and k = 2n+1 to see if the a and b parameters became halved with the increase of temperature (see Bindi et al., Reference Bindi, Keutsch, Francis and Menchetti2009), and two hkl reflections with h and k = 2n (always present) as standard. Subsequently, the temperature was raised to 310 K with a heating rate of 5 K/h, and the same data set was collected. The same procedure was then repeated at 320, 335, 350, 365, 380, 395 and 410 K (Fig. 2). The high (up to 410 K) temperatures were achieved by means of an Oxford cryostream cooler. Unlike what was observed for fettelite, the intensities of the selected reflections with h and k = 2n + 1 (i.e. 151, 352, 17$\bar{3}$![]() , 736) did not change in the temperature range investigated.
, 736) did not change in the temperature range investigated.

Fig. 2. Temperature dependence of the relative intensity of some selected reflections normalised to the value measured at 298 K. For fettelite (left) the intensity of reflections having h and k = 2n +1 becomes very weak when the temperature increases whereas that of reflections having h and k = 2n remains constant. In ferrofettelite (right) the intensity of all the reflections remain constant.
The unit-cell parameters obtained at the different temperatures are reported in Table 3. Before each measurement the sample was maintained at the specified temperature for ~20 min. As a check, the crystal was cooled from 410 K to 335 K. The unit-cell values obtained did not reveal significant variations from the previous one, thus indicating that no hysteresis occurs within the temperature range examined.
Table 3. Unit-cell parameters for the selected ferrofettelite crystal at different temperatures.

*Unit-cell parameters re-measured at 335 K after cooling.
Discussion
Crystal-chemical considerations
As already reported by Bindi et al. (Reference Bindi, Downs, Spry, Pinch and Menchetti2012), the crystal structure of ferrofettelite is nearly identical to that reported previously by Bindi et al. (Reference Bindi, Keutsch, Francis and Menchetti2009) for fettelite. In brief, the structure can be described as the alternation of two kinds of layers along the c-axis (Fig. 3): layer A with general composition [Ag6As2S7]2– (almost identical to that found in the structure of pearceite–polybasite group of minerals; Bindi et al., Reference Bindi, Nespolo, Krivovichev, Chapuis and Biagioni2020) and layer B with a general composition of [Ag10FeAs2S8]2+. In the structure, the Ag atoms adopt various coordinations extending from quasi linear to quasi tetrahedral, the AsS3 groups form pyramids as are typically observed in sulfosalts, and Fe links two sulfur atoms in a linear coordination with mean bond distances of 2.302 and 2.310 Å.

Fig. 3. Projection of the ferrofettelite structure along the monoclinic b axis, emphasizing the succession of the [Ag6As2S7]2– A and [Ag10FeAs2S8]2+ B module layers. White, green, red and yellow circles indicate Ag, As, Fe and S atoms, respectively. The unit-cell and the orientation of the structure are outlined.
Alternatively, the ferrofettelite structure can be described as based on two-atom-thick Ag-enargite-type layers with one S vacancy [i.e. Ag3As(S3□)] (which correspond to pseudo-hexagonal sphalerite-type layers), and an intercalation of a single one-atom-thick Ag4(Fe,Hg)S2 layer (Fig. 4). The (Fe,Hg) atom can be considered as a ‘bridging cation’. The connection between two unit-cells along c is possible with an isolated S atom that acts as inversion centre between two sphalerite-type layers. With this approach, the resulting general formula could be written as [Ag3As(S3□)]2+(S)+[Ag3As(S3□)]2+[Ag4(Fe,Hg)S2], which corresponds to (Ag12As4S12)S[Ag4(Fe,Hg)S2]. Using this modular description, the pearceite–polybasite structure (Bindi et al., Reference Bindi, Nespolo, Krivovichev, Chapuis and Biagioni2020) could be envisioned as composed by two one-atom-thick Ag-enargite-type layers together with two one-atom-thick ‘pure’ Ag layers.

Fig. 4. Modular description of the crystal structure of ferrofettelite. ‘S-type layer’ stands for ‘sphalerite-type layer’ and ‘interc. Layer’ stands for ‘intercalated Ag4(Fe,Hg)S2 layer’. See text for explanations. Symbols and orientation of the structure as in Fig. 3.
The structural positions of the B module layer hosting Fe in ferrofettelite are not fully occupied by Fe but can be written as Fe0.57Hg0.41Cu0.02 (by normalising the population of the site to 1.00). The Fe2+ ↔ Hg substitution is supported by the decrease in the mean bond distances with respect to the fully occupied Hg positions in fettelite, i.e. 2.393 and 2.403 Å, respectively (Bindi et al., Reference Bindi, Keutsch, Francis and Menchetti2009).
A very interesting and peculiar feature in the ferrofettelite structure is the linearly coordinated Fe2+ cation. Even if it is not a fully Fe2+-occupied site, to the best of our knowledge, this is the first inorganic compound having IIFe2+ (as a dominant cation) ever reported. Fe2+ coordinates linearly two sulfur atoms and is hosted in a cavity with four Ag atoms at distances in the range 3.064–3.246 Å and two additional sulfur atoms at distances of 3.051 and 3.431 Å (Fig. 5). There are examples of linearly coordinated Fe2+ with oxygen in complex organic compounds (e.g. Reiff et al., Reference Reiff, Schulz, Whangbo, Seo, Lee, Potratz, Spicer and Girolami2009) or examples of organic complexes with linearly-coordinated monovalent iron with N and C (e.g. Zadrozny et al., Reference Zadrozny, Xiao, Atanasov, Long, Grandjean, Neese and Long2013), but no previously reported examples in inorganic crystal structures. It is very likely that the linear coordination is favoured by the presence of large amounts of Hg at the same sites. Nevertheless, given the importance of Fe2+ in two-fold coordination with S, we have tried to estimate its ionic radius. By plotting the two mean bond distances of the linearly coordinated sites – including also a Cu-enriched fettelite from Germany studied by Bindi et al. (Reference Bindi, Downs, Spry, Pinch and Menchetti2012) exhibiting a chemistry of the (Hg,Cu,Fe) site of Hg0.84Cu0.15Fe0.01 and having mean bond distances of 2.335 and 2.355 Å, and selected members of the pearceite–polybasite group of minerals having Cu sites (Bindi et al., Reference Bindi, Evain and Menchetti2006, Reference Bindi, Evain, Spry and Menchetti2007a, Reference Bindi, Evain and Menchetti2007b, Reference Bindi, Evain, Spry, Tait and Menchetti2007c; Evain et al., Reference Evain, Bindi and Menchetti2006) – against the aggregated ionic radius (i.e. AGIR), we assessed a value for the ionic radius of Fe2+ in two-fold coordination of ~0.50 Å (Fig. 6). A similar value can be obtained by considering the unit-cell volume of the three samples [ferrofettelite: 6071.9 Å3 (this study), Cu-bearing fettelite: 6085.0 Å3 (Bindi et al., Reference Bindi, Downs, Spry, Pinch and Menchetti2012) and fettelite: 6095.2 Å3 (Bindi et al., Reference Bindi, Keutsch, Francis and Menchetti2009)] as a function of the AGIR. Interestingly, a recent machine learning approach carried out to extend the Shannon's ionic radii database (Baloch et al., Reference Baloch, Alqahtani, Mumtaz, Muqaibel, Rashkeev. and Alharbi2021) reported a value of 0.478 Å for IIFe2+, in excellent agreement with that inferred from our crystal-chemical lucubrations.

Fig. 5. A portion (at different orientations) of the crystal structure of ferrofettelite emphasising the Fe2+ coordination sphere. Short bond distances are depicted with a solid lines, long contacts with Ag and additional S atoms are given as dashed lines. The orientation of the structure is outlined. Symbols as in Fig. 3.

Fig. 6. Relationship between the <IIM–S> distances (Å) versus the aggregated ionic radius (AGIR) (Å) for ferrofettelite (this study), German fettelite (Bindi et al., Reference Bindi, Downs, Spry, Pinch and Menchetti2012), Chilean fettelite (Bindi et al., Reference Bindi, Keutsch, Francis and Menchetti2009) and minerals of the pearceite–polybasite group (Bindi et al., Reference Bindi, Evain and Menchetti2006, Reference Bindi, Evain, Spry and Menchetti2007a, Reference Bindi, Evain and Menchetti2007b, Reference Bindi, Evain, Spry, Tait and Menchetti2007c, Reference Bindi, Nespolo, Krivovichev, Chapuis and Biagioni2020; Evain et al., Reference Evain, Bindi and Menchetti2006).
High-temperature behaviour
Bindi and Menchetti (Reference Bindi and Menchetti2011) found that fettelite undergoes an ionic phase transition at ~380 K. In the high-temperature structure, the A module layer is identical to that at room temperature. On the contrary, in the B module layer silver atoms are distributed along a diffusion path thus leading to a quasi-liquid displacement for these ions. This is characteristic of superionic conductors that show a strong disorder in the sub-lattice of the moving cations. As is evident from Fig. 2, ferrofettelite does not undergo any phase transition. It is not clear at the moment why Fe atoms (the only difference with respect to pure fettelite) inhibits the fast-ion conduction. Although it is well known that Hg is more mobile than Fe in ionic conductors, it is hard to think that the presence of iron dominating over Hg in the linear sites can be the only responsible feature. Further experimental work at temperature higher than 410 K will be carried to shed light on the structural behaviour of ferrofettelite.
Supplementary material
To view supplementary material for this article, please visit https://doi.org/10.1180/mgm.2022.28
Acknowledgements
We wish to thank Frantisek Laufek, Yves Moëlo, Stuart Mills and Oleg Siidra for their helpful comments. This research received support by Ministero dell'Istruzione, dell'Università e della Ricerca through the project PRIN 2017 “TEOREM – deciphering geological processes using Terrestrial and Extraterrestrial ORE Minerals”, prot. 2017AK8C32 (PI: Luca Bindi).