Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-26T03:25:20.587Z Has data issue: false hasContentIssue false
  • English
  • Français

Staurolite twinning (With Plates V-VI.)

Published online by Cambridge University Press:  14 March 2018

Vernon J. Hurst ,
J. D. H. Donnay  and
Gabrielle Donnay
Vernon J. Hurst
Affiliation:
The Johns Hopkins University, Baltimore 18, Maryland, U.S.A.
J. D. H. Donnay
Affiliation:
The Johns Hopkins University, Baltimore 18, Maryland, U.S.A.
Gabrielle Donnay
Affiliation:
Geophysical Laboratory, Carnegie Institution of Washington, Washington, D.C., U.S.A.
Get access Rights & Permissions [Opens in a new window]

Summary

The space group Ccmm of the accepted staurolite structure (7·82:16·52:5·63 kX 0·473:1:0·341, Náray-Szabó 1929) is a pseudo-space group; the true one has no c glide plane. Staurolite is monoclinie pseudo-orthorhombic, as shown optically by horizontal dispersion and morphologically by unequal developments of forms r(201) and r′(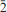01). It has variable cell dimensions, 7·83–7·95:16·50–16·82:5·62 5·71 Å., constant β 90° + 3′, aspect C*, and probable space group C2/m (negative pyroelectric test). This leads to the prediction of a new type of twin, ‘by high order merohedry’, a penetration twin that simulates an orthorhombic single crystal. It is known (Friedel, 1922) that the 90°-cross can be accounted for by two different twin laws and the 60°-cross by five. The twin operations are respectively the pseudo-symmetry operations of a pseudo-tetragonal cell, obtained by transformation 010/003/100, and those of Mallard's pseudo-cube, resulting from transformation 013/0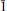3/300. By precession methods more than one twin law is established for each type of cross: both laws [100]90° and [013]180° are found for 90°-crosses: [313]180 and [102]120°, for 60°-crosses.

Type
Research Article
Information
Mineralogical magazine and journal of the Mineralogical Society , Volume 31 , Issue 233 , June 1956 , pp. 145 - 163
Copyright
Copyright © The Mineralogical Society of Great Britain and Ireland 1956

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Biswas, (S. L.), 1928. Quart. Journ. Geol., Min. Met. Soc. India, vol. 1, p. 151 [M.A. 5-37].Google Scholar
Buerger, (M. J.), 1944. The photography of the reciprocal lattice. ASXRED Monograph No. 1 [M.A. 10-10].Google Scholar
Buerger, (M. J.), 1954. Anais Acad. Brasil. Ciencias, vol. 26, p. 111.Google Scholar
Cardoso, (G. M.), 1928. Zeits. Krist., vol. 66, p. 485 [M.A. 3-529].Google Scholar
Dana, (E. S.), 1876. Amer. 5ourn. Sci., ser. 3, vol. 11, p. 384.Google Scholar
Dana, (E. S.), 1892. System of Mineralogy, 6th edn, New York.Google Scholar
Donnay, (Gabrielle) and Donnay, (J. D. H.), 1954. Acta Cryst., vol. 7, p. 619.Google Scholar
Donnay, (Gabrielle) and Donnay, (J. D. H.), and Hurst, (V. J.), 1955. Ibid., vol. 8, p. 507.Google Scholar
Donnay, (J. D. H.), 1938. Ann. (Bull.) Soc. geol. Belg., vol. 61, p. B260 [M.A. 7-242].Google Scholar
Donnay, (J. D. H.), 1939. Amer. Min., vol. 24, p. 184.Google Scholar
Donnay, (J. D. H.), 1947. Bull. Soc. frang. Min., vol. 69, p. 151 (1946) [M.A. 10-466].Google Scholar
Donnay, (J. D. H.), and Harker, (D.), 1937. Amer. Min., vol. 22, p. 446 [M.A. 7-241].Google Scholar
Evans, (R. C.), 1946. An introduction to crystal chemistry, Cambridge.Google Scholar
Friedel, (G.), 1904. Etude sur les groupements cristallins. Bull. Soc. Ind. Min. (4), vols. 3-4. Reprinted in book form, Saint-Etienne, 1904.Google Scholar
Friedel, (G.), 1920. Bull. Soc. franc. Min., vol. 43, p. 246 [M.A. 2-368].Google Scholar
Friedel, (G.), 1922. Ibid., vol. 45, p. 8 [M.A. 2-144].Google Scholar
Friedel, (G.), 1926. Lecons de cristallographie, Paris. (See pp. 245-252 and 421-493.)Google Scholar
Furcron, (A. S.), 1949. The Earth Science Digest, vol. 3, No. 7, p. 7.Google Scholar
Goldschmidt, (V.), 1922. Arias der Kristalfformcn, vol. 8, Heidelberg [M.A. 2-289].Google Scholar
Gottfried, (C.), 1927. Zeits. Krist., vol. 66, p. 103 [M.A. 3-434].Google Scholar
Naray-Szabo, , 1929. Ibid., vol. 71, p. 103 [M.A. 4-160].Google Scholar
Skerl, (A. C.), Bannister, (F. A.), and Groves, (A. W.), 1934. Min. Mag., vol. 23, pp. 598, 633.Google Scholar
Weiss, (K.), 1901. Zeits. Ferdinandeum, Innsbrtick, ser. 3, vol. 45, p. 129.Google Scholar