Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-23T17:42:59.306Z Has data issue: false hasContentIssue false
  • English
  • Français

A simple damage-gradient enhanced elastoplastic formulation andits numerical implementation

Published online by Cambridge University Press:  18 July 2012

Madjid Almansba ,
Khémais Saanouni  and
Naceur Eddine Hannachi
Madjid Almansba*
Affiliation:
ICD/LASMIS, STMR UMR-CNRS 6279, University of Technology of Troyes, 12 rue Marie Curie, BP 2060, 10000 Troyes Cedex, France LAMOMS, Université Mouloud Mammeri Tizi Ouzou, BP 17, Route de Hasnaoua, Tizi Ouzou 15000, Algérie
Khémais Saanouni
Affiliation:
ICD/LASMIS, STMR UMR-CNRS 6279, University of Technology of Troyes, 12 rue Marie Curie, BP 2060, 10000 Troyes Cedex, France
Naceur Eddine Hannachi
Affiliation:
LAMOMS, Université Mouloud Mammeri Tizi Ouzou, BP 17, Route de Hasnaoua, Tizi Ouzou 15000, Algérie
*
⋆ Corresponding author:[email protected]
Get access

Abstract

This paper presents a ductile damage-gradient based nonlocal and fully coupledelastoplastic constitutive equations by adding a Helmholtz equation to regularize theinitial and boundary value problem (IBVP) exhibiting some damage induced softening. First,a thermodynamically-consistent formulation of gradient-regularized plasticity fullycoupled with isotropic ductile damage and accounting for mixed non linear isotropic andkinematic hardening is presented. For the sake of simplicity, only a simplified version ofthis model based on von Mises isotropic yield function and accounting for the singlenonlinear isotropic hardening is studied and implemented numerically using an in house FEcode. An additional partial differential equation governing the evolution of the nonlocalisotropic damage is added to the equilibrium equations and the associated weak formsderived to define the IBVP (initial and boundary value problem). After the time and spacediscretization, two algebraic equations: one highly nonlinear associated with theequilibrium equation and the second purely linear associated with the damage non localityequation are obtained. Over a typical load increment, the first equation is solvediteratively thanks to the Newton-Raphson scheme and the second equation is solved directlyto compute the nonlocal damage \hbox{$\Bar{{D}}$}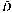D̅ at each node. All the constitutive equations are “strongly” affected bythis nonlocal damage variable transferred to each integration point. Some applicationsshow the ability of the proposed approach to obtain a mesh independent solution for afixed value of the length scale parameter. Comparisons between fully local and nonlocalsolutions are given.

Keywords

Elastoplasticityisotropic hardeningnonlocal damagedamage-behavior couplingdamage gradientnumerical integrationFEMÉlastoplasticitéécrouissageendommagement non localcouplage comportement-endommagementgradient d’endommagementintégration numériqueMEF
Type
Research Article
Information
Mechanics & Industry , Volume 13 , Issue 2 , 2012 , pp. 97 - 110
Copyright
© AFM, EDP Sciences 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Belytschko, T., Chiang, H.Y., Plaskacz, E., High resolution two-dimensional shear band computations : imperfections and mesh dependence, Comput. Methods Appl. Mech. Eng. 137 (1994) 1–15 CrossRefGoogle Scholar
Besson, J., Steglich, D., Brocks, W., Modeling of crack growth in round bars and plane strain specimens, lnt. J. Solids Struct. 38 (2001) 8259–8284 CrossRefGoogle Scholar
Noll, W., Materially uniform simple bodies with inhomogeneities, Arch. Ration. Mech. Anal. 27 (1967) 1–32 CrossRefGoogle Scholar
R.H.J. Peerlings, Enhanced damage modelling for fracture and fatigue, Ph.D. thesis, Technische Universiteit Eindhoven, 1999
B. Nedjar, Elastoplastic modelling including the gradient of damage : formulation and computational aspects, Int. J. Solids struct. (2001) 5421–5451
Geers, M., Ubachs, R., Engelen, R., Strongly non-local gradient-enhanced finite strain elastoplasticity, Int. J. Num. Methods Eng. 56 (2003) 2039–2068 CrossRefGoogle Scholar
Voyiadjis, G.Z. et al., Thermodynamic framework for coupling of non-local viscoplasticity and non-local anisotropic viscodamage for dynamic localization problems using gradient theoriy, Int. J. Plast. 20 (2004) 981–1038 CrossRefGoogle Scholar
Forest, S., Micromorphic Approach for Gradient Elasticity, Viscoplasticity and Damage, J. Eng. Mech. 135 (2009) 117–131 CrossRefGoogle Scholar
Liebe, T., Steinmann, P., Benallal, A., Theoretical and computational aspects of thermodynamically consistent framework for geometrically linear gradient damage, Comput. Methods Appl. Mech. Eng. 190 (2001) 6555–6576 CrossRefGoogle Scholar
J. Lemaitre, A Course on Damage Mechanics [M]. Springer-Verlag, Berlin, 1992
Pamin, J., de Borst, R., Geers, M.G.D., On coupled gradient-dependent plasticity and damage theories with a view to localization analysis, Eur. J. Mech. Appl. Sol. 18 (1999) 939–962 Google Scholar
G.A. Maugin, Remarks on the thermomechanics of weakly noniocal theories [A]. In : Nonlocal Aspects in Solid Mechanics, Abstracts of the EuroMech Colloquium 378 [C]. Mulhouse, France, 1998
Peerlings, R.H.J., Massart, T.J., Geers, M.G.D., A thermodynamical motivated implicit gradient damage framework and its application to brick masonry cracking, Compt. Methods Appl. Mech. Eng. 193 (2004) 3403–3417 CrossRefGoogle Scholar
Boers, S., Schreurs, P., Geers, M., Operator-split damage-plasticity applied to groove forming in food can lids, Int. J. Sol. Struct. 42 (2005) 4154–4178 CrossRefGoogle Scholar
Pijaudier-Cabot, G., Bažant, Z., Nonlocal continuum damage, localization instability and convergence, Int. J. Appl. Mech. 55 (1988) 287–293 Google Scholar
K. Saanouni, Sur l’analyse de la fissuration des milieux élasto-viscoplastiques par la théorie de l’endommagement continue, Thèse de doctorat, Université de Technologie de Compiègne, 1988
Geers, M., Finite strain logarithmic hyperelasto-plasticity with softening : A strongly non-local implicit gradient framework, Comput. Meth. Appl. Mech. Eng. 193 (2004) 3377–3401 CrossRefGoogle Scholar
Forest, S., Sievert, R., Nonlinear microstrain theories, Int. J. Solids Struct. 43 (2006) 7224–7245 CrossRefGoogle Scholar
F. Cosserat, Théorie des corps déformables, 1909
Green, A.E., Rivlin, R.S., Simple force and stress multipoles, Arch. Ration. Mech. Anal. 16 (1964) 325–353 CrossRefGoogle Scholar
Mindlin, R.D., Second gradient of strain and surface–tension in linear elasticity, Int. J. Sol. Struct. 1 (1965) 417–438 CrossRefGoogle Scholar
Eringen, A.C., Balance laws of micromorphic mechanics, Int. J. Eng. Sci. 8 (1970) 819–828 CrossRefGoogle Scholar
Germain, P., La méthode des puissances virtuelles en mécanique des milieux continus, première partie : théorie du second gradient, J. Mécanique 12 (1973) 235–274 Google Scholar
Maugin, G.A., Internal variables and Dissipative Structures, J. Non-Equilibrium Thermodynamics 15 (1990) 173–192 CrossRefGoogle Scholar
K. Saanouni, M. Hamed, M. Almansba, D. Sornin, Damage mechanics nonlocal formulations revisited, 7th Euromech Solids Mechanical Conference, ESMC 2009, Lisbon, Portugal, 2009, pp.7–11
M. Hamed, K. Saanouni, Micromorphic approach for an elastoplastic damage gradient non-local model : Theoretical and computational aspects. 37th Solid Mechanics Conference, Warswa, Poland, 2010, p. 6
Sornin, D., Saanouni, K., About elastoplastic non-local formulations with damage gradients, Int. J. Damage Mech. 20 (2011) 845–875 CrossRefGoogle Scholar
D. Sornin, Sur les formulations élastoplastiques non-locales en gradient d’endommagement, Ph.D. Thesis, UTT, 03 octobre 2007
K. Saanouni, J.L. Chaboche, Computational damage mechanics, in: R. de Borst, H.A. Mang (ed.), Numerical and Computational methods, Vol. 3, chap. 3.06, pp. 321-376, in : I. Milne, R.O. Ritchie, B. Karihaloo (éds), ISBN : 0-08-043749-4, 2003, Elsevier Ltd, Oxford (UK)
Saanouni, K., CH. Forster, F. Ben Hatira, On the anelastic flow with damage, Int. J. Damage Mech. 3 (1994) 140–169 CrossRefGoogle Scholar
D. Sornin, K. Saanouni, Theoretical and computational aspects of an elastoplastic damage gradient nonlocal. III European Conference on Computational Mechanics Solids, Structures and Coupled Problems in Engineering C.A. Mota Soares et al. (eds.) Lisbon, Portugal, 5–8 June 2006
Y. Hammi, Simulation numérique de l’endommagement dans les procédés de mise en forme, Université de Technologie de Compiègne, 2000
Simone, A., Wells, G., Sluys, L., From continuous to discontinuous failure in a gradient-enhanced continuum damage model, Comput. Meth. Appl. Mech. Eng. 192 (2003) 4581–4607 CrossRefGoogle Scholar
D.R.J. Owen, E. Hinton, Finite elements in plasticity, theory and practice, ed. Pineridge Press Limited, 1988