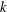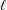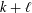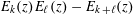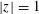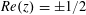Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Brazelton, Thomas
and
Jakicic, Victoria
2018.
Zeros of newform Eisenstein series on Γ0(N).
Journal of Number Theory,
Vol. 190,
Issue. ,
p.
109.
Klangwang, Jetjaroen
2019.
Zeros of certain combinations of Eisenstein series of weight 2k,3k, and k + l.
Journal of Number Theory,
Vol. 198,
Issue. ,
p.
124.
Choi, SoYoung
and
Im, Bo-Hae
2021.
The number of zeros of certain combinations of the Eisenstein series for Γ0+(2).
Journal of Number Theory,
Vol. 223,
Issue. ,
p.
101.
Xue, Hui
and
Zhu, Daozhou
2021.
Location of the zeros of certain cuspforms.
International Journal of Number Theory,
Vol. 17,
Issue. 08,
p.
1899.
Xue, Hui
and
Zhu, Daozhou
2023.
Double interlacing between zeros of modular forms.
The Ramanujan Journal,
Vol. 60,
Issue. 2,
p.
463.
Kimmel, Noam
2024.
Asymptotic Zeros of Poincaré Series.
International Mathematics Research Notices,
Vol. 2024,
Issue. 21,
p.
13808.
Choi, SoYoung
and
Im, Bo-Hae
2024.
Zeros of the combination of the Eisenstein series for $$\Gamma _0^+(2)$$.
The Ramanujan Journal,
Vol. 64,
Issue. 2,
p.
475.
Choi, SoYoung
and
Im, Bo-Hae
2024.
Location and double interlacing of zeros of certain combination of the Eisenstein series for Γ0+(2).
Journal of Mathematical Analysis and Applications,
Vol. 537,
Issue. 2,
p.
128397.
van Ittersum, Jan‐Willem
and
Ringeling, Berend
2025.
On the zeros of odd weight Eisenstein series.
Mathematika,
Vol. 71,
Issue. 1,