Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Benjamin, T. Brooke
1995.
Verification of the Benjamin–Lighthill conjecture about steady water waves.
Journal of Fluid Mechanics,
Vol. 295,
Issue. -1,
p.
337.
Doole, S. H.
and
Norbury, J.
1995.
The bifurcation of steady gravity water waves in (R, S) parameter space.
Journal of Fluid Mechanics,
Vol. 302,
Issue. ,
p.
287.
Kozlov, Vladimir
and
Kuznetsov, Nikolay
2012.
Bounds for steady water waves with vorticity.
Journal of Differential Equations,
Vol. 252,
Issue. 1,
p.
663.
Kozlov, Vladimir
and
Kuznetsov, Nikolay
2013.
No steady water waves of small amplitude are supported by a shear flow with a still free surface.
Journal of Fluid Mechanics,
Vol. 717,
Issue. ,
p.
523.
Kozlov, Vladimir
and
Kuznetsov, Nikolay
2013.
Steady water waves with vorticity: spatial Hamiltonian structure.
Journal of Fluid Mechanics,
Vol. 733,
Issue. ,
Wheeler, Miles H.
2013.
Large-Amplitude Solitary Water Waves with Vorticity.
SIAM Journal on Mathematical Analysis,
Vol. 45,
Issue. 5,
p.
2937.
Kozlov, Vladimir
and
Kuznetsov, Nikolay
2014.
Dispersion Equation for Water Waves with Vorticity and Stokes Waves on Flows with Counter-Currents.
Archive for Rational Mechanics and Analysis,
Vol. 214,
Issue. 3,
p.
971.
Kozlov, V.
Kuznetsov, N.
and
Lokharu, E.
2014.
Steady water waves with vorticity: an analysis of the dispersion equation.
Journal of Fluid Mechanics,
Vol. 751,
Issue. ,
Kozlov, V.
Kuznetsov, N.
and
Lokharu, E.
2015.
On bounds and non-existence in the problem of steady waves with vorticity.
Journal of Fluid Mechanics,
Vol. 765,
Issue. ,
Kozlov, V.
Kuznetsov, N.
and
Lokharu, E.
2017.
On the Benjamin–Lighthill conjecture for water waves with vorticity.
Journal of Fluid Mechanics,
Vol. 825,
Issue. ,
p.
961.
Kozlov, V
and
Kuznetsov, N
2017.
Bounds for Solutions to the Problem of Steady Water Waves with Vorticity.
The Quarterly Journal of Mechanics and Applied Mathematics,
Vol. 70,
Issue. 4,
p.
497.
Walsh, Samuel
Wheeler, Miles H.
and
Chen, Robin Ming
2018.
Existence and qualitative theory for stratified solitary water waves.
Annales de l'Institut Henri Poincaré C, Analyse non linéaire,
Vol. 35,
Issue. 2,
p.
517.
Kozlov, Vladimir
and
Lokharu, Evgeniy
2018.
N-Modal Steady Water Waves with Vorticity.
Journal of Mathematical Fluid Mechanics,
Vol. 20,
Issue. 2,
p.
853.
Basu, Biswajit
2020.
A flow force reformulation for steady irrotational water waves.
Journal of Differential Equations,
Vol. 268,
Issue. 12,
p.
7417.
Basu, Biswajit
and
Martin, Calin-I.
2020.
Capillary-gravity water waves: Modified flow force formulation.
Journal of Differential Equations,
Vol. 269,
Issue. 12,
p.
11231.
Basu, Biswajit
and
Martin, Calin I.
2021.
An alternative approach to study irrotational periodic gravity water waves.
Zeitschrift für angewandte Mathematik und Physik,
Vol. 72,
Issue. 4,
Chu, Jifeng
Wang, Xun
Wang, Ling-Jun
and
Zhang, Zhi
2021.
A flow force reformulation of steady periodic fixed-depth irrotational equatorial flows.
Journal of Differential Equations,
Vol. 292,
Issue. ,
p.
220.
Basu, Biswajit
and
Kogelbauer, Florian
2021.
Global bifurcation of irrotational water waves using a flow force formulation.
Journal of Differential Equations,
Vol. 301,
Issue. ,
p.
73.
Lokharu, Evgeniy
2021.
On the amplitude and the flow force constant of steady water waves.
Journal of Fluid Mechanics,
Vol. 921,
Issue. ,
Lokharu, Evgeniy
2024.
A Sharp Version of the Benjamin and Lighthill Conjecture for Steady Waves with Vorticity.
Journal of Mathematical Fluid Mechanics,
Vol. 26,
Issue. 2,
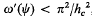 , where hc is the height of the crest of the wave.
, where hc is the height of the crest of the wave.

