Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-23T05:25:28.614Z Has data issue: false hasContentIssue false
  • English
  • Français

WARING’S PROBLEM WITH SHIFTS

Part of: Additive number theory; partitions Diophantine equations Forms and linear algebraic groups

Published online by Cambridge University Press:  06 March 2015

Sam Chow
Sam Chow*
Affiliation:
School of Mathematics, University of Bristol, University Walk, Clifton, Bristol BS8 1TW, U.K. email [email protected]
Get access

Abstract

Let 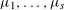${\it\mu}_{1},\ldots ,{\it\mu}_{s}$ be real numbers, with 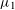${\it\mu}_{1}$ irrational. We investigate sums of shifted 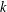$k$th powers 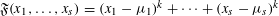$\mathfrak{F}(x_{1},\ldots ,x_{s})=(x_{1}-{\it\mu}_{1})^{k}+\cdots +(x_{s}-{\it\mu}_{s})^{k}$. For 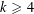$k\geqslant 4$, we bound the number of variables needed to ensure that if 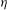${\it\eta}$ is real and 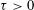${\it\tau}>0$ is sufficiently large then there exist integers 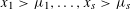$x_{1}>{\it\mu}_{1},\ldots ,x_{s}>{\it\mu}_{s}$ such that 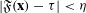$|\mathfrak{F}(\mathbf{x})-{\it\tau}|<{\it\eta}$. This is a real analogue to Waring’s problem. When 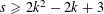$s\geqslant 2k^{2}-2k+3$, we provide an asymptotic formula. We prove similar results for sums of general univariate degree-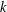$k$ polynomials.

MSC classification

Primary: 11D75: Diophantine inequalities
Secondary: 11E76: Forms of degree higher than two 11P05: Waring's problem and variants
Type
Research Article
Information
Mathematika , Volume 62 , Issue 1 , 2016 , pp. 13 - 46
Copyright
Copyright © University College London 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baker, R. C., Diophantine Inequalities (London Mathematical Society Monographs (N.S.) 1), Clarendon Press (Oxford, 1986).Google Scholar
Brüdern, J., Kawada, K. and Wooley, T. D., Additive representation in thin sequences, VIII: Diophantine inequalities in review. In Number Theory, 20–79 (Series on Number Theory and its Applications 6), World Scientific (Hackensack, NJ, 2010).Google Scholar
Chow, S., Cubic diophantine inequalities for split forms. Monatsh. Math. 175 2014, 213–225.CrossRefGoogle Scholar
Chow, S., Sums of cubes with shifts. J. Lond. Math. Soc. (2) 2015, doi:10.1112/jlms/jdu077.CrossRefGoogle Scholar
Davenport, H., Analytic Methods for Diophantine Equations and Diophantine Inequalities, 2nd edn., Cambridge University Press (Cambridge, 2005).CrossRefGoogle Scholar
Davenport, H. and Heilbronn, H., On indefinite quadratic forms in five variables. J. Lond. Math. Soc. 21 1946, 185–193.CrossRefGoogle Scholar
Freeman, D. E., One cubic diophantine inequality. J. Lond. Math. Soc. (2) 61(1) 2000, 25–35.CrossRefGoogle Scholar
Freeman, D. E., Asymptotic lower bounds and formulas for Diophantine inequalities. In Number Theory for the Millennium II, A. K. Peters (Natick, MA, 2002), 57–74.Google Scholar
Freeman, D. E., Additive inhomogeneous Diophantine inequalities. Acta Arith. 107(3) 2003, 209–244.CrossRefGoogle Scholar
Götze, F., Lattice point problems and values of quadratic forms. Invent. Math. 157(1) 2004, 195–226.CrossRefGoogle Scholar
Hardy, G. H. and Littlewood, J. E., Some problems of “Partitio numerorum” (VI): further researches in Waring’s problem. Math. Z. 23(1) 1925, 1–37.CrossRefGoogle Scholar
Harvey, M. P., Cubic Diophantine inequalities involving a norm form. Int. J. Number Theory 7(8) 2011, 2219–2235.CrossRefGoogle Scholar
Margulis, G. A., Discrete subgroups and ergodic theory. In Number Theory, Trace Formulas and Discrete Groups (Oslo, 1987), Academic Press (Boston, MA, 1989), 377–398.Google Scholar
Margulis, G. A. and Mohammadi, A., Quantitative version of the Oppenheim conjecture for inhomogeneous quadratic forms. Duke Math. J. 158(1) 2011, 121–160.CrossRefGoogle Scholar
Marklof, J., Pair correlation densities of inhomogeneous quadratic forms. Ann. of Math. (2) 158(2) 2003, 419–471.CrossRefGoogle Scholar
Nathanson, M. B., Elementary Methods in Number Theory (Graduate Texts in Mathematics 195), Springer (New York, 2000).Google Scholar
Parsell, S. T. and Wooley, T. D., Exceptional sets for Diophantine inequalities. Int. Math. Res. Not. IMRN 2014(14) 2014, 3919–3974.CrossRefGoogle Scholar
Schmidt, W. M., Diophantine inequalities for forms of odd degree. Adv. Math. 38(2) 1980, 128–151.CrossRefGoogle Scholar
Vaughan, R. C., On Waring’s problem for sixth powers. J. Lond. Math. Soc. (2) 33(2) 1986, 227–236.CrossRefGoogle Scholar
Vaughan, R. C., On Waring’s problem for smaller exponents. Proc. Lond. Math. Soc. (3) 52(3) 1986, 445–463.CrossRefGoogle Scholar
Vaughan, R. C., The Hardy–Littlewood Method, 2nd edn., Cambridge University Press (Cambridge, 1997).CrossRefGoogle Scholar
Vaughan, R. C. and Wooley, T. D., Waring’s problem: a survey. In Number Theory for the Millennium III, A. K. Peters (Natick, MA, 2002), 301–340.Google Scholar
Waring, E., Meditationes Arithmeticæ, 2nd edn., Archdeacon (Cambridge, 1770).Google Scholar
Wooley, T. D., On Diophantine inequalities: Freeman’s asymptotic formulae. In Proceedings of the Session in Analytic Number Theory and Diophantine Equations (Bonner Mathematische Schriften 360), University of Bonn (Bonn, 2003).Google Scholar
Wooley, T. D., Multigrade efficient congruencing and Vinogradov’s mean value theorem (submitted), Preprint, 2013, arXiv:1310.8447.Google Scholar