Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-23T15:38:11.506Z Has data issue: false hasContentIssue false
  • English
  • Français

Uniform bounds for the least almost-prime primitive root

Part of: Multiplicative number theory

Published online by Cambridge University Press:  26 February 2010

Greg Martin
Greg Martin
Affiliation:
School of Mathematics, Institute for Advanced Study, Princeton, NJ 08540, U.S.A.
Get access

Extract

A recurring theme in number theory is that multiplicative and additive properties of integers are more or less independent of each other, the classical result in this vein being Dirichlet's theorem on primes in arithmetic progressions. Since the set of primitive roots to a given modulus is a union of arithmetic progressions, it is natural to study the distribution of prime primitive roots. Results concerning upper bounds for the least prime primitive root to a given modulus q, which we denote by g*(q), have hitherto been of three types. There are conditional bounds: assuming the Generalized Riemann Hypothesis, Shoup [11] has shown that

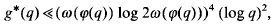
where ω(n) denotes the number of distinct prime factors of n. There are also upper bounds that hold for almost all moduli q. For instance, one can show [9] that for all but O(Y∈) primes up to Y, we have

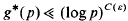
for some positive constant C(∈). Finally, one can apply a much stronger result, a uniform upper bound for the least prime in a single arithmetic progression. The best uniform result of this type, due to Heath-Brown [7], implies that 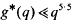. However, there is not at present any stronger unconditional upper bound for g*(q) that holds uniformly for all moduli q. The purpose of this paper is to provide such an upper bound, at least for primitive roots that are “almost prime”.

MSC classification

Secondary: 11N25: Distribution of integers with specified multiplicative constraints
Type
Research Article
Information
Mathematika , Volume 45 , Issue 1 , June 1998 , pp. 191 - 207
Copyright
Copyright © University College London 1998

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Burgess, D. A.. On character sums and L-series II. Proc. London Math. Soc. (3), 13 (1963), 524–536.CrossRefGoogle Scholar
2.Greaves, G.. A weighted sieve of Brun's type. Ada Arith., 40 (1982), 297–332.CrossRefGoogle Scholar
3.Greaves, G.. The weighted linear sieve and Selberg's λ2-method. Ada Arith., 47 (1986), 71–96.CrossRefGoogle Scholar
4.Halberstam, H. and Richert, H.-E.. Sieve methods (Academic Press, London, 1974).Google Scholar
5.Heath-Brown, D. R.. Prime twins and Siegel zeroes. Proc. London Math. Soc. (3), 47 (1983), no. 2, 193–224.CrossRefGoogle Scholar
6.Heath-Brown, D. R.. Siegel zeroes and the least prime in an arithmetic progression. Quart. J. Math. Oxford, 41, (1990), 405–418.CrossRefGoogle Scholar
7.Heath-Brown, D. R.. Zero-free regions for Dirichlet L-functions, and the least prime in an arithmetic progression. Proc. London Math. Soc. (3), 64 (1992), 265–338.CrossRefGoogle Scholar
8.Kruswijk, D.. On the congruence up − 1 ≡ 1 modulo p2. Math. Centrum Amsterdam Afd. Zuivere Wisk. ZW-003.Google Scholar
9.Martin, G.. The least prime primitive root and the shifted sieve, Ada Arith., 80 (1997), 277–288.Google Scholar
10.Mikawa, H.. Almost-primes in arithmetic progressions and short intervals. Tsukuba J. Math., 13 (1989), 387–401.CrossRefGoogle Scholar
11.Shoup, V.. Searching for primitive roots in finite fields. Math. Comp., 58 (1992), 369–380.CrossRefGoogle Scholar