Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-23T17:55:09.664Z Has data issue: false hasContentIssue false
  • English
  • Français

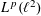A TWO-WEIGHT INEQUALITY BETWEEN $L^{p}(\ell ^{2})$ AND 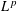$L^{p}$

Part of: Harmonic analysis in several variables

Published online by Cambridge University Press:  14 February 2018

Tuomas Hytönen  and
Emil Vuorinen
Tuomas Hytönen
Affiliation:
Department of Mathematics and Statistics, P.O.B. 68 (Gustaf Hällströmin katu 2b), FI-00014 University of Helsinki, Finland email [email protected]
Emil Vuorinen
Affiliation:
Department of Mathematics and Statistics, P.O.B. 68 (Gustaf Hällströmin katu 2b), FI-00014 University of Helsinki, Finland email [email protected]
Get access

Abstract

We consider boundedness of a certain positive dyadic operator

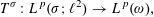$$\begin{eqnarray}T^{\unicode[STIX]{x1D70E}}:L^{p}(\unicode[STIX]{x1D70E};\ell ^{2})\rightarrow L^{p}(\unicode[STIX]{x1D714}),\end{eqnarray}$$
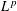that arose during our attempts to develop a two-weight theory for the Hilbert transform in $L^{p}$. Boundedness of 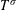$T^{\unicode[STIX]{x1D70E}}$ is characterized when 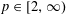$p\in [2,\infty )$ in terms of certain testing conditions. This requires a new Carleson-type embedding theorem that is also proved.

MSC classification

Primary: 42B20: Singular and oscillatory integrals (Calderón-Zygmund, etc.)
Type
Research Article
Information
Mathematika , Volume 64 , Issue 1 , 2018 , pp. 284 - 302
Copyright
Copyright © University College London 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Hänninen, T. S., Hytönen, T. P. and Li., K., Two-weight L p –L q bounds for positive dyadic operators: unified approach to p⩽q and p > q . Potential Anal. 45(3) 2016, 579–608.CrossRefGoogle Scholar
Hytönen, T. P., The two-weight inequality for the Hilbert transform with general measures. Preprint, 2013, arXiv:1312.0843.Google Scholar
Hytönen, T. P., The A 2 theorem: remarks and complements. In Harmonic Analysis and Partial Differential Equations (Contemporary Mathematics 612 ), American Mathematical Society (Providence, RI, 2014), 91–106.Google Scholar
Lacey, M. T., Two-weight inequality for the Hilbert transform: a real variable characterization, II. Duke Math. J. 163(15) 2014, 2821–2840.Google Scholar
Lacey, M. T., Sawyer, E. T., Shen, C.-Y. and Uriarte-Tuero, I., Two-weight inequality for the Hilbert transform: a real variable characterization, I. Duke Math. J. 163(15) 2014, 2795–2820.Google Scholar
Lacey, M. T., Sawyer, E. T. and Uriarte-Tuero, I., Two weight inequalities for discrete positive operators. Preprint, 2009, arXiv:0911.3437.Google Scholar
Marcinkiewicz, J. and Zygmund, A., Quelques inégalités pour les opérations linéaires. Fund. Math. 32 1939, 115–121.Google Scholar
Nazarov, F., Treil, S. and Volberg, A., The Bellman functions and two-weight inequalities for Haar multipliers. J. Amer. Math. Soc. 12(4) 1999, 909–928.Google Scholar
Sawyer, E. T., A characterization of two weight norm inequalities for fractional and Poisson integrals. Trans. Amer. Math. Soc. 308(2) 1988, 533–545.Google Scholar
Tanaka, H., A characterization of two-weight trace inequalities for positive dyadic operators in the upper triangle case. Potential Anal. 41(2) 2014, 487–499.Google Scholar
Vuorinen, E., L p (𝜇)→L q (𝜈) characterization for well localized operators. J. Fourier Anal. Appl. 22(5) 2016, 1059–1075.Google Scholar
Vuorinen, E., Two-weight L p -inequalities for dyadic shifts and the dyadic square function. Studia Math. 237(1) 2017, 25–56.Google Scholar