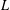Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-26T15:54:10.726Z Has data issue: false hasContentIssue false
  • English
  • Français

TRUNCATED PRODUCT REPRESENTATIONS FOR $L$-FUNCTIONS IN THE HYPERELLIPTIC ENSEMBLE

Part of: Arithmetic problems. Diophantine geometry Zeta and $L$-functions: analytic theory Arithmetic algebraic geometry

Published online by Cambridge University Press:  06 February 2018

J. C. Andrade ,
S. M. Gonek  and
J. P. Keating
J. C. Andrade
Affiliation:
Department of Mathematics, University of Exeter, North Park Road, Exeter EX4 4QF, U.K. email [email protected]
S. M. Gonek
Affiliation:
Department of Mathematics, University of Rochester, Rochester, NY 14627, U.S.A. email [email protected]
J. P. Keating
Affiliation:
School of Mathematics, University of Bristol, Bristol BS8 1TW, U.K. email [email protected]
Get access

Abstract

We investigate the approximation of quadratic Dirichlet 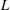$L$-functions over function fields by truncations of their Euler products. We first establish representations for such 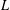$L$-functions as products over prime polynomials times products over their zeros. This is the hybrid formula in function fields. We then prove that partial Euler products are good approximations of an 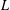$L$-function away from its zeros and that, when the length of the product tends to infinity, we recover the original 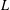$L$-function. We also obtain explicit expressions for the arguments of quadratic Dirichlet 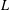$L$-functions over function fields and for the arguments of their partial Euler products. In the second part of the paper we construct, for each quadratic Dirichlet 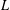$L$-function over a function field, an auxiliary function based on the approximate functional equation that equals the 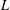$L$-function on the critical line. We also construct a parametrized family of approximations of these auxiliary functions and prove that the Riemann hypothesis holds for them and that their zeros are related to those of the associated 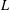$L$-function. Finally, we estimate the counting function for the zeros of this family of approximations, show that these zeros cluster near those of the associated 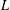$L$-function, and that, when the parameter is not too large, almost all the zeros of the approximations are simple.

MSC classification

Primary: 11G20: Curves over finite and local fields
Secondary: 14G10: Zeta-functions and related questions (Birch-Swinnerton-Dyer conjecture) 11M50: Relations with random matrices
Type
Research Article
Information
Mathematika , Volume 64 , Issue 1 , 2018 , pp. 137 - 158
Copyright
Copyright © University College London 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Artin, E., Quadratische Körper in Geibiet der Höheren Kongruzzen I and II. Math. Z. 19 1924, 153–296.Google Scholar
Bogomolny, E. B. and Keating, J. P., Gutzwiller’s trace formula and spectral statistics: beyond the diagonal approximation. Phys. Rev. Lett. 77 1996, 1472–1475.Google Scholar
Bui, H. and Florea, A., Hybrid Euler–Hadamard product for quadratic Dirichlet $L$ -functions in function fields. Preprint, 2016, arXiv:1609.05363.Google Scholar
Bui, H. M. and Keating, J. P., On the mean values of Dirichlet L-functions. Proc. Lond. Math. Soc. (3) 95 2007, 273–298.Google Scholar
Bui, H. M. and Keating, J. P., On the mean values of L-functions in orthogonal and symplectic families. Proc. Lond. Math. Soc. (3) 96 2008, 335–366.Google Scholar
Faifman, D., Counting zeros of $L$ -functions over the rational function field. MSc Thesis, Tel Aviv University, 2008.Google Scholar
Faifman, D. and Rudnick, Z., Statistics of the zeros of zeta functions in families of hyperelliptic curves over a finite field. Compositio. Math. 146 2010, 81–101.Google Scholar
Farmer, D., Gonek, S. M. and Hughes, C., The maximum size of L-functions. J. Reine Angew. Math. 609 2007, 215–236.Google Scholar
Gonek, S. M., Finite Euler products and the Riemann hypothesis. Trans. Amer. Math. Soc. 364 2012, 2157–2191.Google Scholar
Gonek, S. M., A note on finite Euler product approximations of the Riemann zeta-function. Proc. Amer. Math. Soc. 143 2015, 3295–3302.Google Scholar
Gonek, S. M., Hughes, C. and Keating, J. P., A hybrid Euler–Hadamard product for the Riemann zeta function. Duke Math. J. 136 2007, 507–549.CrossRefGoogle Scholar
Montgomery, H. L., Ten Lectures on the Interface between Analytic Number Theory and Harmonic Analysis, American Mathematical Society (Providence, RI, 1994).Google Scholar
Montgomery, H. L. and Vaughan, R. C., Multiplicative Number Theory I: Classical Theory, Cambridge University Press (Cambridge, 2007).Google Scholar
Rosen, M., Number Theory in Function Fields (Graduate Texts in Mathematics 210 ), Springer (New York, 2002).Google Scholar
Thakur, D. S., Function Field Arithmetic, World Scientific (NJ, 2004).Google Scholar
Titchmarsh, E. C., The Theory of the Riemann Zeta-function, 2nd edn. (ed. Heath-Brown, D. R.), The Clarendon Press, Oxford University Press (New York, 1986).Google Scholar
Weil, A., Sur les Courbes Algébriques et les Variétés qui s’en Déduisent, Hermann (Paris, 1948).Google Scholar