Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-26T17:13:08.881Z Has data issue: false hasContentIssue false
  • English
  • Français

TIGHTER BOUNDS FOR THE DISCREPANCY OF BOXES AND POLYTOPES

Part of: Harmonic analysis in several variables Polytopes and polyhedra Probabilistic theory: distribution modulo $1$; metric theory of algorithms

Published online by Cambridge University Press:  29 November 2017

Aleksandar Nikolov
Aleksandar Nikolov*
Affiliation:
Department of Computer Science, University of Toronto, Toronto, Canada email [email protected]
Get access

Abstract

Combinatorial discrepancy is a complexity measure of a collection of sets which quantifies how well the sets in the collection can be simultaneously balanced. More precisely, we are given an $n$-point set 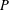$P$, and a collection 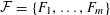${\mathcal{F}}=\{F_{1},\ldots ,F_{m}\}$ of subsets of 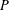$P$, and our goal is color 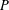$P$ with two colors, red and blue, so that the maximum over the 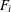$F_{i}$ of the absolute difference between the number of red elements and the number of blue elements (the discrepancy) is minimized. Combinatorial discrepancy has many applications in mathematics and computer science, including constructions of uniformly distributed point sets, and lower bounds for data structures and private data analysis algorithms. We investigate the combinatorial discrepancy of geometrically defined systems, in which 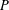$P$ is an $n$-point set in 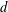$d$-dimensional space, and 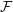${\mathcal{F}}$ is the collection of subsets of 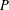$P$ induced by dilations and translations of a fixed convex polytope 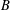$B$. Such set systems include systems of sets induced by axis-aligned boxes, whose discrepancy is the subject of the well-known Tusnády problem. We prove new discrepancy upper and lower bounds for such set systems by extending the approach based on factorization norms previously used by the author, Matoušek, and Talwar. We also outline applications of our results to geometric discrepancy, data structure lower bounds, and differential privacy.

MSC classification

Primary: 11K38: Irregularities of distribution, discrepancy
Secondary: 52B11: $n$-dimensional polytopes 42B05: Fourier series and coefficients
Type
Research Article
Information
Mathematika , Volume 63 , Issue 3 , 2017 , pp. 1091 - 1113
Copyright
Copyright © University College London 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aistleitner, C., Bilyk, D. and Nikolov, A., Tusnády’s problem, the transference principle, and non-uniform QMC sampling. CoRR Preprint, 2017, arXiv:1703.06127.CrossRefGoogle Scholar
Alexander, R., Principles of a new method in the study of irregularities of distribution. Invent. Math. 103(2) 1991, 279–296.Google Scholar
Banaszczyk, W., Balancing vectors and Gaussian measures of n-dimensional convex bodies. Random Structures Algorithms 12(4) 1998, 351–360.Google Scholar
Banaszczyk, W., On series of signed vectors and their rearrangements. Random Structures Algorithms 40(3) 2012, 301–316.Google Scholar
Bansal, N., Dadush, D. and Garg, S., An algorithm for Komlós conjecture matching Banaszczyk’s bound. In IEEE 57th Annual Symposium on Foundations of Computer Science, FOCS 2016, 9–11 October 2016, Hyatt Regency, New Brunswick, New Jersey, U.S.A. (ed. Dinur, I.), IEEE Computer Society (Washington, DC, 2016), 788–799.Google Scholar
Bansal, N. and Garg, S., Algorithmic discrepancy beyond partial coloring. In Proceedings of the 49th Annual ACM SIGACT Symposium on Theory of Computing (STOC 2017), ACM (New York, NY, 2017).Google Scholar
Beck, J., Balanced two-colorings of finite sets in the square. I. Combinatorica 1 1981, 327–335.Google Scholar
Beck, J. and Chen, W. W. L., Irregularities of Distribution (Cambridge Tracts in Mathematics 89 ), Cambridge University Press (Cambridge, 2008). Reprint of the 1987 original [MR 0903025].Google Scholar
Bilyk, D., Lacey, M. T. and Vagharshakyan, A., On the small ball inequality in all dimensions. J. Funct. Anal. 254(9) 2008, 2470–2502.Google Scholar
Brandolini, L., Colzani, L. and Travaglini, G., Average decay of Fourier transforms and integer points in polyhedra. Ark. Mat. 35(2) 1997, 253–275.Google Scholar
Charikar, M., Newman, A. and Nikolov, A., Tight hardness results for minimizing discrepancy. In Proceedings of the Twenty-Second Annual ACM-SIAM Symposium on Discrete Algorithms, SODA 2011, San Francisco, California, USA, January 23–25, 2011 (ed. Randall, D.), SIAM (Philadelphia, PA, 2011), 1607–1614.Google Scholar
Chazelle, B., Randomness and complexity. In The Discrepancy Method, Cambridge University Press (Cambridge, 2000).CrossRefGoogle Scholar
Drmota, M., Irregularities of distributions with respect to polytopes. Mathematika 43(1) 1996, 108–119.Google Scholar
Dwork, C., Mcsherry, F., Nissim, K. and Smith, A., Calibrating noise to sensitivity in private data analysis. In Theory of Cryptography (Lecture Notes in Computer Science 3876 ), Springer (Berlin, 2006), 265–284.CrossRefGoogle Scholar
Dwork, C. and Roth, A., The algorithmic foundations of differential privacy. Found. Trends Theor. Comput. Sci. 9(3–4) 2014, 211–407.Google Scholar
Epstein, C. L., How well does the finite Fourier transform approximate the Fourier transform? Comm. Pure Appl. Math. 58(10) 2005, 1421–1435.CrossRefGoogle Scholar
Fredman, M. L., The complexity of maintaining an array and computing its partial sums. J. ACM 29(1) 1982, 250–260.Google Scholar
Götz, M., Discrepancy and the error in integration. Monatsh. Math. 136(2) 2002, 99–121.Google Scholar
Halton, J. H., On the efficiency of certain quasi-random sequences of points in evaluating multi-dimensional integrals. Numer. Math. 2 1960, 84–90.CrossRefGoogle Scholar
Hammersley, J. M., Monte Carlo methods for solving multivariable problems. Ann. New York Acad. Sci. 86 1960, 844–874.Google Scholar
Judin, V. A., A multidimensional Jackson theorem. Mat. Zametki 20(3) 1976, 439–444. Presented at the International Conference on the Theory of Approximation of Functions, held at Kaluga, July 24–28, 1975.Google Scholar
Larsen, K. G., On range searching in the group model and combinatorial discrepancy. SIAM J. Comput. 43(2) 2014, 673–686.Google Scholar
Lee, T., Shraibman, A. and Špalek, R., A direct product theorem for discrepancy. In Proceedings of the 23rd Annual IEEE Conference on Computational Complexity, CCC 2008, 23–26 June 2008, College Park, Maryland, U.S.A., IEEE Computer Society (Washington, DC, 2008), 71–80.Google Scholar
Linial, N., Mendelson, S., Schechtman, G. and Shraibman, A., Complexity measures of sign matrices. Combinatorica 27(4) 2007, 439–463.Google Scholar
Matoušek, J., On the discrepancy for boxes and polytopes. Monatsh. Math. 127(4) 1999, 325–336.Google Scholar
Matoušek, J., Geometric Discrepancy (Algorithms and Combinatorics 18 ), Springer (Berlin, 2010). An illustrated guide, Revised paperback reprint of the 1999 original.Google Scholar
Matoušek, J. and Nikolov, A., Combinatorial discrepancy for boxes via the 𝛾2 norm. In 31st International Symposium on Computational Geometry (SoCG 2015) (LIPIcs, Leibniz International Proceedings in Informatics 34 ), Schloss Dagstuhl–Leibniz Center for Informatics (2015), 1–15.Google Scholar
Matoušek, J., Nikolov, A. and Talwar, K., Factorization norms and hereditary discrepancy. CoRR Preprint, 2015, arXiv:1408.1376v2.Google Scholar
Nikolov, A., New computational aspects of discrepancy theory. PhD Thesis, Rutgers, The State University of New Jersey, 2014.Google Scholar
Nikolov, A. and Talwar, K., Approximating hereditary discrepancy via small width ellipsoids. In Proceedings of the Twenty-Sixth Annual ACM-SIAM Symposium on Discrete Algorithms, SODA 2015, San Diego, CA, U.S.A., January 4–6, 2015 (ed. Indyk, P.), SIAM (Philadelphia, PA, 2015), 324–336.Google Scholar
Nikolov, A., Talwar, K. and Zhang, L., The geometry of differential privacy: the small database and approximate cases. SIAM J. Comput. 45(2) 2016, 575–616.CrossRefGoogle Scholar
Roth, K. F., On irregularities of distribution. Mathematika 1 1954, 73–79.Google Scholar
Roth, K. F., Remark concerning integer sequences. Acta Arith. 9 1964, 257–260.Google Scholar
Schmidt, W. M., Irregularities of distribution. VII. Acta Arith. 21 1972, 45–50.Google Scholar
Tomczak-Jaegermann, N., Banach-Mazur Distances and Finite-Dimensional Operator Ideals (Pitman Monographs and Surveys in Pure and Applied Mathematics 38 ), Wiley (New York, 1989).Google Scholar