Published online by Cambridge University Press: 26 February 2010
Let Ω be a compact metric space of non-σ-finite Λh-measure, where Λh denotes the Hausdorff measure corresponding to some continuous increasing real function h(t), denned for t ≥ 0 and with h(t) > 0 and h(t) > 0 for t > 0. C. A. Rogers has drawn attention to two problems that have remained unsolved for some years, and which seem to present considerable difficulty:
I. Does Ω necessarily have subsets of finite positive Λh-measure?
II. Does Ω. necessarily contain a system of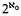 disjoint closed subsets each of non-σ-finite Λh-measure ?
disjoint closed subsets each of non-σ-finite Λh-measure ?
The answers are affirmative when Ω is a subset of a Euclidean space (see [1], [2], [3], [4], [5]); recently D. G. Larman ([8], [9]) was able to extend each of these results to the case of the “finite-dimensional” compact metric spaces that he introduced in [7]. Both of his proofs depend on the detailed structure of such spaces; the aim of the present paper is to establish a general theorem, from which it follows in particular that Larman's second result is a consequence of his first, and that an affirmative answer to I would imply an affirmative answer to II. (Since it seems likely that I must be answered negatively in general, and II affirmatively, the present theorem may well be of only ephemeral significance; the nature of the proof reinforces this expectation.)