Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-09T15:07:11.714Z Has data issue: false hasContentIssue false
  • English
  • Français

Sums and products of functions in the MacLane class A

Published online by Cambridge University Press:  26 February 2010

D. A. Brannan  and
R. Hornblower
D. A. Brannan
Affiliation:
University of Maryland, and Imperial College, London
R. Hornblower
Affiliation:
University of Maryland, and Imperial College, London
Get access

Extract

Let 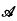be the class of non-constant functions f(z), holomorphic in |z| < 1, which have asymptotic values at a dense set of points on |z| = 1. MacLane [4; p. 18] asked whether the sum and product of two functions in 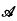had to be either constant or in 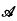. Recently Barth and Ryan [2] have shown that this was not necessarily so; in this note we will demonstrate, in a totally elementary way, why not. Our principal result is:

Theorem 1. Any non-constant function R(z), holomorphic in |z| < 1, may be represented both as a sum and as a product of pairs of functions in.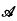

Type
Research Article
Information
Mathematika , Volume 16 , Issue 1 , June 1969 , pp. 86 - 87
Copyright
Copyright © University College London 1969

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Barth, K. F., “Asymptotic values of meromorphic functions”, Mich. Math. J., 13 (1966), 321–340.CrossRefGoogle Scholar
2.Barth, K. F. and Ryan, F. B., “Asymptotic values of functions holomorphic in the unit disc”, Math. Zeit., 100 (1967), 414–415.Google Scholar
3.Heins, M., Selected topics in the classical theory of functions of a complex variable (Holt, Rinehart and Winston, New York, 1962).Google Scholar
4.MacLane, G. R., Asymptotic values of holomorphic functions, Rice Univ. Studies, Vol. 49, No. 1, Winter 1963.Google Scholar
5.Hornblower, R., “On a class of functions regular in the unit disc”, Proc. Camb. Phil. Soc., 64 (1968), 651–654.CrossRefGoogle Scholar