Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-23T19:31:32.756Z Has data issue: false hasContentIssue false
  • English
  • Français

Sums and differences of quartic norms

Part of: Multiplicative number theory

Published online by Cambridge University Press:  26 February 2010

Henryk Iwaniec  and
Jacek Pomykala
Henryk Iwaniec
Affiliation:
Department of Mathematics, Rutgers University, New Brunswick, NJ 08903, USA.
Jacek Pomykala
Affiliation:
Institute of Mathematics, Warsaw University, 00-950 Warsaw, Poland.
Get access

Extract

Let K be a number field of degree k > 1. We would like to know if a positive integer N can be represented as the sum, or the difference, of two norms of integral ideals of K. Suppose K/ℚ is abelian of conductor Δ. Then from the class field theory (Artin's reciprocity law) the norms are fully characterized by the residue classes modulo Δ. Precisely, a prime number p ∤ Δ (unramified in K) is a norm (splits completely in K), if, and only if,

where k is a subgroup of (ℤ/Δℤ)* of index k. Accordingly we may ask N to be represented as the sum

or the difference

of positive integers a, b each of which splits completely in K. For N to be represented in these ways the following congruences

must be solvable in α β є k, respectively. Moreover the condition

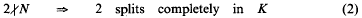
must hold. Presumably the above local conditions are sufficient for (−) to have infinitely many solutions and for (+) to have arbitrarily many solutions, provided N is sufficiently large in the latter case.

MSC classification

Secondary: 11N36: Applications of sieve methods
Type
Research Article
Information
Mathematika , Volume 40 , Issue 2 , December 1993 , pp. 233 - 245
Copyright
Copyright © University College London 1993

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Bombieri, E., Friedlander, J. and Iwaniec, H.. Primes in arithmetic progressions to large moduli. Acta Math., 156 (1986), 203–251.CrossRefGoogle Scholar
2.Birch, B.J., Davenport, H. and Lewis, D. J.. The addition of norm forms. Mathematika, 9 (1962), 75–82.CrossRefGoogle Scholar
3.Chen, J. R.. On the representation of a large even integer as the sum of a prime and the product of at most two primes (in Chinese). Kexua Tangbao, 17 (1966), 385–38.Google Scholar
4.Chen, J. R.. On the representation of a large even integer as the sum of a prime and the product of at most two primes. Sci. Sinica, 16 (1973), 157–176.Google Scholar
5.Deshouillers, J.-M. and Iwaniec, H.. Kloosterman sums and Fourier coefficients of cusp forms. Invent. Math., 70 (1982), 219–288.CrossRefGoogle Scholar
6.Fouvry, E.. Autour du Théorème de Bombieri-Vinogradov, II. Ann. scient. Éc. Norm. Sup., 20 (1987), 617–640.CrossRefGoogle Scholar
7.Halberstam, H. and Richert, E. H.. Sieve methods (Academic Press, London 1974).Google Scholar
8. H. Iwaniec. Primes of the type φ(x, y) + A, where φ is a quadratic form. Acta Arith., 21 (1972), 203–234.CrossRefGoogle Scholar
9.Iwaniec, H.. On sums of two norms from cubic fields. Journées de théorie additive des nombres, Bordeaux, 1977.Google Scholar
10.Iwaniec, H.. Rosser's sieve. Acta Arith., 36 (1980), 171–202.CrossRefGoogle Scholar
11.Mertens, F.. Über einige asymptotische Gesetze der Zahlentheorie. J. reine und angew. Math., 77 (1874), 289–338.Google Scholar
12.Wirsing, E.. Das asymptotische Verhalten von Summen über multiplicative Funktionen, I. Math. Ann., 143 (1961), 75–102.CrossRefGoogle Scholar