Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-03T04:55:08.181Z Has data issue: false hasContentIssue false
  • English
  • Français

Structure of l-class groups of certain number fields and ℤl-extensions

Published online by Cambridge University Press:  26 February 2010

Frank Gerth III
Frank Gerth III
Affiliation:
Department of MathematicsThe Universtity of Texas, Austin, Texas 78712, U. S. A.
Get access

Extract

Let l be a rational prime, and let ℤl denote the ring of l-adic integers. Let k0 be a finite extension field of the rational numbers ℚ, and let K be a ℤl-extension of k0 (i.e., Gal (K/k0) is topologically isomorphic to the additive group of Zl). Let the intermediate fields be denoted as follows:

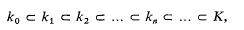
where knk0 is a cyclic extension of degree ln, and 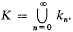Let An denote the l-class group of kn (i.e., the Sylow l-subgroup of the ideal class group of kn). It is known that the order of An is given by 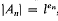, with

Type
Research Article
Information
Mathematika , Volume 24 , Issue 1 , June 1977 , pp. 16 - 33
Copyright
Copyright © University College London 1977

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Gold, R.. “Examples of Iwasawa invariants”, Acta Arithmetica, 26 (1974), 21–32.CrossRefGoogle Scholar
2.Greenberg, R.. On some questions concerning the Iwasawa invariants, Ph.D. Thesis, (Princeton University, 1971).Google Scholar
3.Iwasawa, K.. “On Zl-extensions of algebraic number fields”, Ann. Math., 98 (1973), 246–326.CrossRefGoogle Scholar
4.Johnson, W.. “Irregular primes and cyclotomic invariants” Math. Comp., 29 (1975), 113–120.CrossRefGoogle Scholar
5.Yokoi, H.. “On the class number of a relatively cyclic number field”, Nagoya Math. J., 29 (1967), 31–44.CrossRefGoogle Scholar
6.Zink, W.. Über die Klassengruppe einer absolut zyklischen Erweiterung, Dissertation, (Humboldt- Universität, Berlin, 1973).Google Scholar