Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-26T17:47:34.346Z Has data issue: false hasContentIssue false
  • English
  • Français

STABLY FREE MODULES OVER 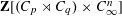$\mathbf{Z}[(C_{p}\rtimes C_{q})\times C_{\infty }^{n}]$ ARE FREE

Part of: Rings and algebras arising under various constructions Grothendieck groups and $K_0$

Published online by Cambridge University Press:  22 February 2017

J. D. P. Evans
J. D. P. Evans*
Affiliation:
Department of Mathematics, University College London, Gower Street, London WC1E 6BT, U.K. email [email protected]
Get access

Abstract

Let 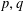$p,q$ be primes such that 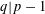$q|p-1$ and set 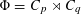$\unicode[STIX]{x1D6F7}=C_{p}\rtimes C_{q}$, 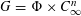$G=\unicode[STIX]{x1D6F7}\times C_{\infty }^{n}$ and 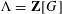$\unicode[STIX]{x1D6EC}=\mathbf{Z}[G]$, the integral group ring of 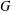$G$. By means of a fibre square decomposition, we show that stably free modules over 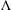$\unicode[STIX]{x1D6EC}$ are necessarily free.

MSC classification

Primary: 19A13: Stability for projective modules
Secondary: 16S34: Group rings , Laurent polynomial rings
Type
Research Article
Information
Mathematika , Volume 63 , Issue 2 , 2017 , pp. 451 - 461
Copyright
Copyright © University College London 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Cohn, P. M., Some remarks on the invariant basis property. Topology 5(3) 1966, 215–228.Google Scholar
Cohn, P. M., Free Rings and Their Relations, Academic Press (San Diego, CA, 1971).Google Scholar
Curtis, C. W. and Reiner, I., Methods of Representation Theory, Vol. 2, Wiley (New York, 1994).Google Scholar
Gabel, M. R., Stably free projectives over commutative rings. PhD Thesis, Brandeis University, 1972.Google Scholar
Johnson, F. E. A., Stable Modules and the D(2)-Problem, Cambridge University Press (Cambridge, 2003).Google Scholar
Johnson, F. E. A., Syzygies and Homotopy Theory, Vol. 17, Springer (London, 2011).Google Scholar
Johnson, F. E. A., Stably free cancellation for abelian group rings. Arch. Math. 102 2014, 7–10.CrossRefGoogle Scholar
Remez, J. J., Diagonal resolutions for the metacyclic groups G(pq). PhD Thesis, University College London, 2012.Google Scholar
Rosen, M., Representations of twisted group rings. PhD Thesis, Princeton University, 1963.Google Scholar
Suslin, A. A., On the structure of the special linear group over polynomial rings. Math. USSR Izvestija 11(2) 1977, 221–238.Google Scholar