No CrossRef data available.
Article contents
Some relations connecting measures of convergence for series with non-increasing terms
Published online by Cambridge University Press: 26 February 2010
Extract
Let an be a non-increasing real sequence such that 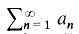 converges; then clearly an ↓ 0. We shall ignore the trivial case where an = 0 for all large n, and so we assume that an > 0 for all n, from now onwards. In [1] J. B. Wilker introduced certain new sequences associated with the rate of convergence of
converges; then clearly an ↓ 0. We shall ignore the trivial case where an = 0 for all large n, and so we assume that an > 0 for all n, from now onwards. In [1] J. B. Wilker introduced certain new sequences associated with the rate of convergence of 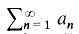 , and obtained various relations between them, in order to investigate packing problems in convex geometry. Let us define
, and obtained various relations between them, in order to investigate packing problems in convex geometry. Let us define
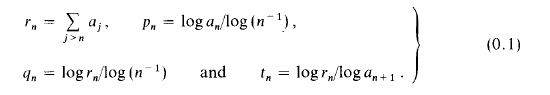
We write P, Q and T respectively for the inferior limits of pn, qn and tn, and P1, Q1 and T1 for the corresponding superior limits. Further, we put
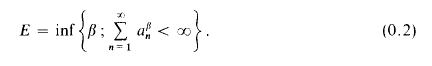
It is immediately clear from these definitions and our assumptions about an that
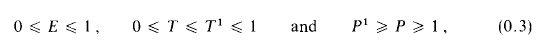
the latter since nan → 0 by Olivier's theorem [2, p. 124].
MSC classification
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 1984


