Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-23T11:41:55.406Z Has data issue: false hasContentIssue false
  • English
  • Français

Some examples of Borel-inseparable pairs of coanalylic sets

Part of: Connections with other structures, applications

Published online by Cambridge University Press:  26 February 2010

Howard Becker
Howard Becker
Affiliation:
Department of Mathematics, University of South Carolina, Columbia, South Carolina, 29208, U.S.A.
Get access

Extract

The purpose of this paper is to give some natural examples of Borel-inseparable pairs of coanalytic sets in Polish spaces.

A Polish space is a topological space homeomorphic to a separable complete metric space. In this paper, all spaces are uncountable Polish spaces. A pointset is analytic (or 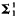) if it is the continuous image of a Borel set (in any space), or equivalently, the projection of a Borel set, and is coanalytic (or ) if it is the complement of an analytic set. The class of analytic sets is closed under countable unions and intersections, images and preimages by Borel measurable functions, and projections; it is not closed under complements, hence there is an analytic set which is not Borel.

MSC classification

Secondary: 54H05: Descriptive set theory (topological aspects of Borel, analytic, projective, etc. sets)
Type
Research Article
Information
Mathematika , Volume 33 , Issue 1 , June 1986 , pp. 72 - 79
Copyright
Copyright © University College London 1986

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Ajtai, M. and Kechris, A. S.. The set of continuous functions with everywhere convergent Fourier series. To appear in Trans. Amer. Math. Soc.Google Scholar
2.Becker, H.. Path-connectedness, simple connectedness and the projective hierarchy. To appear.Google Scholar
3.Bourgain, J.. The Szlenk index and operators on C(K)-spaces. Bull. Soc. Math. Belg. Ser. B., 31 (1979), 87–117.Google Scholar
4.Dellacherie, C. and Meyer, P. A.. Ensembles analytiques et temps d'arrêt, in Séminaire de Probabilités IX, Lecture Notes in Math., vol. 465, Ed. Meyer, P. A. (Springer-Verlag, Berlin and New York, 1975), 373–389.Google Scholar
5.Grzegorczyk, A., Mostowski, A. and Ryll-Nardzewski, C.. The classical and the ω-complete arithmetic. J. Symbolic Logic, 23 (1958), 188–206.CrossRefGoogle Scholar
6.Hurewicz, W.. Zur Theorie der analytischen Mengen. Fund. Math., 15 (1930), 4–17.Google Scholar
7.Kechris, A. S., Sets of everywhere singular functions. In Recursion Theory Week, Lecture Notes in Math., 1141, Ed. Ebbinghaus, H.-D., Müller, G. H. and Sacks, G. E. (Springer, Berlin, 1985), 233–244.Google Scholar
8.Kechris, A. S.. Examples of sets and norms. Lecture notes, Oberwolfach recursion theory conference, 1984.Google Scholar
9.Kechris, A. S. and Woodin, W. H.. Ranks of differentiable functions. To appear.Google Scholar
10.Kuratowski, K.. Topology, Vol. I (Academic Press, New York and London, 1966).Google Scholar
11.Lusin, N.. Leçons sur les Ensembles Analytiques et leur Applications, 2nd edition (Chelsea, New York, 1972).Google Scholar
12.Martin, D. A. and Kechris, A. S.. Infinite games and effective descriptive set theory, in [16].Google Scholar
13.Mauldin, D.. The set of continuous nowhere differentiable functions. Pacific J. Math., 83 (1979), 199–205.Google Scholar
14.Mazurkiewicz, S.. Über die Menge der differenzierbaren Funktionen. Fund. Math., 27 (1936), 244–249.Google Scholar
15.Moschovakis, Y. N.. Descriptive Set Theory (North-Holland, Amsterdam, 1980).Google Scholar
16.Rogers, C. A. et al. Analytic Sets (Academic Press, New York, 1980).Google Scholar
17.Zahorski, Z.. Sur l'ensemble des points de non-derivabilite d'une fonction continue. Bull. Soc. Math. France, 74 (1946), 147–178.Google Scholar