Article contents
Solvability in Lp of the Neumann problem for a singular non-homogeneous Sturm-Liouville equation
Published online by Cambridge University Press: 26 February 2010
Abstract
Consider the equation
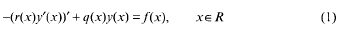
where 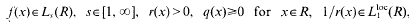 ,
, 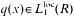 . The inversion problem for (1) is called regular in Lp if, uniformly in p∈[1, ∞] for any f(x)∈ Lp(R), equation (1) has a unique solution y(x)∈ Lp(R) of the form
. The inversion problem for (1) is called regular in Lp if, uniformly in p∈[1, ∞] for any f(x)∈ Lp(R), equation (1) has a unique solution y(x)∈ Lp(R) of the form
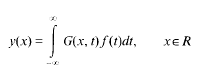
with 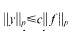 . Here G(x, t) is the Green function corresponding to (1) and c is an absolute constant. For a given s∈[l, ∞], necessary and sufficient conditions are obtained for assertions (2) and (3) to hold simultaneously:
. Here G(x, t) is the Green function corresponding to (1) and c is an absolute constant. For a given s∈[l, ∞], necessary and sufficient conditions are obtained for assertions (2) and (3) to hold simultaneously:
(2) the inversion problem for (1) is regular in Lp;
(3) 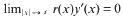 for any f(x)∈LS(R).
for any f(x)∈LS(R).
MSC classification
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 1999
References
- 2
- Cited by


