Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-23T18:49:39.621Z Has data issue: false hasContentIssue false
  • English
  • Français

Small zeros of quadratic congruences modulo pq

Published online by Cambridge University Press:  26 February 2010

Todd Cochrane
Todd Cochrane
Affiliation:
Department of Mathematics, Kansas State University, Cardwell Hall, Manhattan, Kansas 66506-2602, U.S.A.
Get access

Extract

Let Q(x) = Q(x1, x2,…, xn) be a quadratic form with integer coefficients. Schinzel, Schickewei and Schmidt [9, Theorem 1] have shown that for any modulus m there exists a nonzero 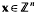such that

and ║x║≤m(1/2)+(1/2(n-1)), where ║x║ = max |xi|. When m is a prime Heath-Brown [8] has obtained a nonzero solution of (1) with ║x║≤m1/2 log m. Yuan [10] has extended Heath-Brown's work to all finite fields. We have proved related results in [5] and [6]. In this paper we extend Heath-Brown's work to moduli which are a product of two primes. Throughout the paper we shall assume that n is even and n>2. For any odd prime p let

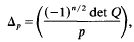
where det Q is the determinant of the integer matrix representing Q and 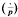is the Legendre symbol.

Type
Research Article
Information
Mathematika , Volume 37 , Issue 2 , December 1990 , pp. 261 - 272
Copyright
Copyright © University College London 1990

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Borevich, Z. I. and Shafarevich, I. R.. Number Theory (Academic Press, New York, 1966).Google Scholar
2. Carlitz, L.. Weighted quadratic partitions over a finite field. Can. J. of Math., 5 (1953), 317–323.CrossRefGoogle Scholar
3. Cochrane, T.. Small Solution of Congruences, Dissertation (The University of Michigan, 1984).Google Scholar
4. Cochrane, T.. Small solutions of congruences over algebraic number fields. III. J. of Math., 31 (1987), 618–625.Google Scholar
5. Cochrane, T.. Small zeros of quadratic forms modulo p. J. of Number Theory, 33 (1989), 286–292.Google Scholar
6. Cochrane, T.. Small zeros of quadratic forms modul p II. To appear.Google Scholar
7. Fujiwara, M.. Distribution of rational points on varieties over finite fields. Mathematika, 35 (1988), 155–171.CrossRefGoogle Scholar
8. Heath-Brown, D. R.. Small solutions of quadratic congruences. Glasgow Math. J., 27 (1985), 87–93.CrossRefGoogle Scholar
9. Schinzel, A., Schlickewei, H. P. and Schmidt, W. M.. Small solutions of quadratic congruences and small fractional parts of quadratic forms. Acta Arithmetica, 37 (1980), 241–248.Google Scholar
10. Yuan, W.. On small zeros of quadratic forms over finite fields. J. of Number Theory, 31 (1989), 272–284.Google Scholar