Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-23T14:26:46.351Z Has data issue: false hasContentIssue false
  • English
  • Français

Skeleta and sections of convex bodies

Part of: General convexity

Published online by Cambridge University Press:  26 February 2010

G. R. Burton
G. R. Burton
Affiliation:
University College London, Gower Street, London WC1E 6BT.
Get access

Extract

The purpose of this paper is to prove two integralgeometric formulae for convex bodies. Our results are expressed in terms of integrals with respect to the rigid-motion-invariant measure μd, r on the space ℰ(d, r) of all r-dimensional affine flats in d-dimensional Euclidean space Ed. Rolf Schneider, in an unpublished note [6], has shown that for a convex polytope P in Ed and 1 ≤ r ≤ d – 1 one has

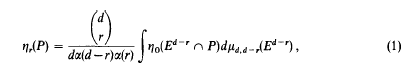
where ηr(P) is the sum of the contents of the r-dimensional faces of P, ηo(Ed–r ∩ P) is the number of vertices of the (d – r)-dimensional section Ed–r ∩ P, and α(r) is the content of the r-dimensional unit ball.

MSC classification

Secondary: 52A22: Random convex sets and integral geometry
Type
Research Article
Information
Mathematika , Volume 27 , Issue 1 , June 1980 , pp. 97 - 103
Copyright
Copyright © University College London 1980

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Burton, G. R.. “The measure of the s-skeleton of a convex body”, Mathematika, 26 (1979), 290–301.CrossRefGoogle Scholar
2.Dalla, L. and Larman, D. G.. “Convex bodies with almost all fc-dimensional sections polytopes”, Math. Proc. Camb. Phil. Soc, to appear.Google Scholar
3.Federer, H.. Geometric measure theory (Springer–Verlag, Berlin, 1969).Google Scholar
4.Santalò, L.. Integral geometry and geometric probability, Encyclopedia of Mathematics and its Applications, vol. 1 (Addison-Wesley, Reading, Massachusetts, 1976).Google Scholar
5.Schneider, R.. “On the skeletons of convex bodies”, Bull. London Math. Soc, 10 (1978), 84–85.CrossRefGoogle Scholar
6.Schneider, R.. “Convex bodies with many polytopal sections”, unpublished.Google Scholar
7.Schneider, R.. “Boundary structure and curvature of convex bodies”, Contributions to geometry (ed. Tölke, J. and Wills, J. M.; Birkhäuser-Verlag, Basel, 1979).Google Scholar