Article contents
Simple one-point extensions of tournaments
Published online by Cambridge University Press: 26 February 2010
Extract
A tournament 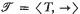 is a relational structure on the non-empty set T such that for x, y ∈ T exactly one of the three relations
is a relational structure on the non-empty set T such that for x, y ∈ T exactly one of the three relations
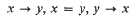
holds. Here x → y expresses the fact that {x, y} ∈ → and we sometimes write this in the alternative form y ← x. Extending the notation to subsets of T we write A → B or B ← A if a → b holds for all pairs a, b with a ∈ A and b ∈ B. 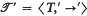 is a subtournament of
is a subtournament of 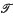 , and
, and 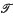 is an extension of
is an extension of 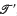 , if T′ ⊂ T and →′ is the restriction of → to T′; we will usually write 〈′, → 〉 instead of 〈 ′, → ′〉. In particular, if |T − T′| = k, we call
, if T′ ⊂ T and →′ is the restriction of → to T′; we will usually write 〈′, → 〉 instead of 〈 ′, → ′〉. In particular, if |T − T′| = k, we call 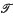 a k-poinf extension of
a k-poinf extension of 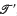 .
.
MSC classification
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 1972
References
- 11
- Cited by


