Hostname: page-component-745bb68f8f-b6zl4 Total loading time: 0 Render date: 2025-01-11T08:59:08.044Z Has data issue: false hasContentIssue false
  • English
  • Français

Sign changes of error terms related to the Euler function

Part of: Multiplicative number theory

Published online by Cambridge University Press:  26 February 2010

Yuk-Kam Lau
Yuk-Kam Lau
Affiliation:
Department of Mathematics, The University of Hong Kong, Pokfulam Road, Hone Kong.
Get access

Extract

Let φ(n) be the Euler function (i.e., φ(n) denotes the number of integers less than n which are relatively prime to n), and define

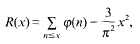
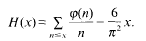
These functions were extensively studied by several mathematicians. One of the problems investigated concerns their sign changes. We say that a function fx) has a sign change at x = x0 if f(x0 −) f(x0 +) < 0, and f(x) has a sign change on the integer n if (n)f(n+1) < 0. The numbers of sign changes and sign changes on integers of f(x) in the interval [1, T] are denoted by Xf(T) and Nf(T), respectively.

MSC classification

Secondary: 11N64: Other results on the distribution of values or the characterization of arithmetic functions
Type
Research Article
Information
Mathematika , Volume 46 , Issue 2 , December 1999 , pp. 391 - 395
Copyright
Copyright © University College London 1999

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ch. Chowla, S., Contributions to the analytic theory of numbers. Math. Z., 35 (1932), 279–299.CrossRefGoogle Scholar
ESI. Erdos, P. and Shapiro, H. M. On the changes of sign of a certain error function. Canad. J. Math. 3 (1951), 375–385.CrossRefGoogle Scholar
ES2. Erdos, P. and Shapiro, H. M. The existence of a distribution function for an error term related to the Euler function. Canad. J. Math., 1 (1955), 63–75.CrossRefGoogle Scholar
Pél. Petermann, Y.-F. S.. Changes of sign of error terms related to Euler's function and to divisor functions. Comm. Math. Helvet., 61 (1986), 84–101.CrossRefGoogle Scholar
Pé2. Petermann, Y.-F. S.. Changes of sign of error terms related to Euler's function and to divisor functions II. Ada Arith., 51 (1988), 321–333.CrossRefGoogle Scholar
Pe3. Pétermann, Y.-F. S.. On the distribution of values of an error term related to the Euler function. Théorie des nombres (Quebec, PQ, 1987), (de Gruyter, Berlin, 1989), pp. 785–797.Google Scholar