Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-24T02:18:56.717Z Has data issue: false hasContentIssue false
  • English
  • Français

A SIEVE PROBLEM AND ITS APPLICATION

Part of: Multiplicative number theory

Published online by Cambridge University Press:  27 September 2016

Andreas Weingartner
Andreas Weingartner*
Affiliation:
Department of Mathematics, Southern Utah University, 351 West University Boulevard, Cedar City, UT 84720, U.S.A. email [email protected]
Get access

Abstract

Let $\unicode[STIX]{x1D703}$ be an arithmetic function and let 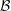${\mathcal{B}}$ be the set of positive integers 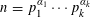$n=p_{1}^{\unicode[STIX]{x1D6FC}_{1}}\cdots p_{k}^{\unicode[STIX]{x1D6FC}_{k}}$ which satisfy 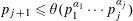$p_{j+1}\leqslant \unicode[STIX]{x1D703}(p_{1}^{\unicode[STIX]{x1D6FC}_{1}}\cdots p_{j}^{\unicode[STIX]{x1D6FC}_{j}})$ for 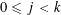$0\leqslant j<k$. We show that 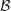${\mathcal{B}}$ has a natural density, provide a criterion to determine whether this density is positive, and give various estimates for the counting function of 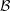${\mathcal{B}}$. When 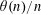$\unicode[STIX]{x1D703}(n)/n$ is non-decreasing, the set 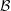${\mathcal{B}}$ coincides with the set of integers $n$ whose divisors 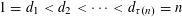$1=d_{1}<d_{2}<\cdots <d_{\unicode[STIX]{x1D70F}(n)}=n$ satisfy 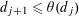$d_{j+1}\leqslant \unicode[STIX]{x1D703}(d_{j})$ for 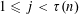$1\leqslant j<\unicode[STIX]{x1D70F}(n)$.

MSC classification

Primary: 11N25: Distribution of integers with specified multiplicative constraints
Type
Research Article
Information
Mathematika , Volume 63 , Issue 1 , 2017 , pp. 213 - 229
Copyright
Copyright © University College London 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Cheer, A. Y. and Goldston, D. A., A differential delay equation arising from the sieve of Eratosthenes. Math. Comp. 55 1990, 129–141.CrossRefGoogle Scholar
Pomerance, C., Thompson, L. and Weingartner, A., On integers $n$ for which $X^{n}-1$ has a divisor of every degree. Acta Arith. (to appear), doi:10.4064/aa8354-6-2016.CrossRefGoogle Scholar
Rosser, J. B. and Schoenfeld, L., Approximate formulas for some functions of prime numbers. Illinois J. Math. 6 1962, 64–94.Google Scholar
Saias, E., Entiers à diviseurs denses 1. J. Number Theory 62 1997, 163–191.CrossRefGoogle Scholar
Tenenbaum, G., Sur un problème de crible et ses applications. Ann. Sci. Éc. Norm. Supér. (4) 19 1986, 1–30.Google Scholar
Thompson, L., Polynomials with divisors of every degree. J. Number Theory 132 2012, 1038–1053.CrossRefGoogle Scholar
Thompson, L., Variations on a question concerning the degrees of divisors of x n - 1. J. Théor. Nombres Bordeaux 26 2014, 253–267.CrossRefGoogle Scholar
Weingartner, A., Practical numbers and the distribution of divisors. Q. J. Math. 66 2015, 743–758.Google Scholar