Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-05T04:15:18.204Z Has data issue: false hasContentIssue false
  • English
  • Français

A sharp inequality related to Moser's inequality

Part of: Real functions

Published online by Cambridge University Press:  26 February 2010

P. C. McCarthy
P. C. McCarthy
Affiliation:
Department of Mathematics, University CollegeCork, Ireland
Get access

Extract

In this paper we shall be concerned with the growth of functions in the class ℳp, where we write f ∈ ℳp 1 <p<∞, if:

(i) f is absolutely continuous on bounded subintervals of [0, ∞]);

(ii) f(0) = 0; and

(iii) .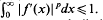

MSC classification

Secondary: 26A46: Absolutely continuous functions
Type
Research Article
Information
Mathematika , Volume 40 , Issue 2 , December 1993 , pp. 357 - 366
Copyright
Copyright © University College London 1993

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Carleson, L. and Chang, S.-Y. A.. On the existence of an extremal for an inequality of J. Moser. Bull, des Science, 110 (1986), 113–127.Google Scholar
2.Garsia, A.. Personal correspondence to J. Moser. March 29, 1972.Google Scholar
3.Jodeit, M.. An inequality for the indefinite integral of a function in Lq. Studia Math., 44 (1972), 545–554.Google Scholar
4.Marshall, D. E.. A new proof of a sharp inequality concerning the Dirichlet integral. Arkiv. Mat., 27 (1989), 131–137.CrossRefGoogle Scholar
5.Moser, J.. A sharp form of an inequality by N. Trudinger. Ind. V. Math. J., 20 (1971), 1077–1092.CrossRefGoogle Scholar