Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-23T18:04:55.449Z Has data issue: false hasContentIssue false
  • English
  • Français

The second moment of the complexity of a graph

Published online by Cambridge University Press:  26 February 2010

J. W. Moon
J. W. Moon
Affiliation:
University College, and London.
Get access

Extract

A graph consists of a set of vertices some pairs of which are joined by a single edge. A tree is a graph with the property that each pair of vertices is connected by precisely one path, i.e., a sequence of distinct vertices joined consecutively by edges. The complexity c of a graph G(n, k) with n vertices and k edges is the number of trees with n vertices which are subgraphs of G(n, k). The distribution of c over the class of all graphs G(n, k) is of physical interest because it throws light on the classical many-body problem. (See, e.g. 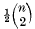[9].) Ford and Uhlenbeck [3] gave numerical data which suggested that the distribution of c tends to normality for increasing n if k is near No moments higher than the first were known in general and they remarked in [4] that even “the second would be worth knowing”. The main object in this paper is to derive a formula for the second moment of c.

Type
Research Article
Information
Mathematika , Volume 11 , Issue 2 , December 1964 , pp. 95 - 98
Copyright
Copyright © University College London 1964

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Bromwich, T. J., An introduction to the theory of infinite series (Macmillan, London, 1931), 136.Google Scholar
2. Cayley, A., “A theorem on trees”, Quart. J. Pure Appl. Math., 23 (1889), 376–378.Google Scholar
3. Ford, G. W. and Uhlenbeck, G. E., “The theory of linear graphs with applications to the virial development of the properties of gases”, Studies in statistical mechanics, I (North-Holland, Amsterdam, 1962), 119–211.Google Scholar
4. Ford, G. W. and Uhlenbeck, G. E., Lectures in statistical mechanics (American Math. Soc., Providence, 1963), 53.Google Scholar
5. Moon, J. W., “Various proofs of Cayley's formula for counting trees”, to appear in A seminar on graph theory, ed. by Harary, F., (Holt, Boston).Google Scholar
6. Pόlya, G. and Szegö, G., Aufgaben und Lehrsätze aus der Analysis, I (Springer, Berlin, 1925), 125.Google Scholar
7. Prüfer, A., “Neuer Beweis eines Satzes über Permutationen”, Arch. Math. Phys., 27 (1918), 142–144.Google Scholar
8. Rényi, A.. “Some remarks on the theory of trees”, Publ. Math. Inst. Hung. Acad. Sci., 4 (1959), 73–85.Google Scholar
9. Temperley, H. N. V., “On the mutual cancellation of cluster integrals in Mayer's fugacity series”, Proc. Phys. Soc., 83 (1964), 3–16.CrossRefGoogle Scholar