Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-05T02:06:15.005Z Has data issue: false hasContentIssue false
  • English
  • Français

Sausage-skin problems for finite coverings

Published online by Cambridge University Press:  26 February 2010

Gábor Fejes Tóth ,
Peter Gritzmann  and
Jörg M. Wills
Gábor Fejes Tóth
Affiliation:
Math. Inst. Hungar. Acad. Sciences, Reáltanoda u. 13–15, H-1053 Budapest.
Peter Gritzmann
Affiliation:
Math. Inst. Univ. Siegen, Hölderlinstrasse, 3, D-5900, Siegen, W. Germany.
Jörg M. Wills
Affiliation:
Math. Inst. Univ. Siegen, Hölderlinstrasse, 3, D-5900, Siegen, W. Germany.
Get access

Extract

Let 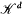denote the set of convex bodies of Ed, i.e. the set of all compact convex subsets of Ed. Let Bi be the unit i-ball, ωi its volume and Si-1 the unit sphere bd Bi. For an arbitrary 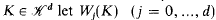denote the j-th quermassintegral (for definition and properties compare [7]). A different normalization of the functionals Wo, …, Wd leads to the intrinsic volumes Vj (which were introduced in [9]) defined by 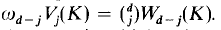The intrinsic volumes are independent of the dimension of the space in which K is embedded. In particular, V0(K) = 1, Vd-1 (K) is half the surface area of K and Vd{K) = V(K) is its volume.

Type
Research Article
Information
Mathematika , Volume 31 , Issue 1 , June 1984 , pp. 117 - 136
Copyright
Copyright © University College London 1984

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Bambah, R. P. and Rogers, C. A.. Covering the plane with convex sets. J. London Math. Soc., 27 (1952), 304–314.CrossRefGoogle Scholar
2.Betke, U., Gritzmann, P. and Wills, J. M.. Slices of L. Fejes Tóth's sausage conjecture. Mathematika, 29 (1982), 194–201.CrossRefGoogle Scholar
3.Tóth, G. Fejes. New results in the theory of packing and covering. In Gruber, P. M., Wills, J. M. (Eds.) Convexity and its Applications (1983), 318–359 (Birkhäuser-Verlag, Basel, Boston, Stuttgart).CrossRefGoogle Scholar
4.Tóth, L. Fejes. Lagerungen in der Ebene, auf der Kugel und im Raum (Springer-Verlag, Berlin, Heidelberg, New York, 2. Aufl., 1972).CrossRefGoogle Scholar
5.Tóth, L. Fejes. Research problem 13. Periodica Math. Hung., 6 (1975), 197–199.Google Scholar
6.Gritzmann, P.. Finite Packungen und Überdeckungen (Siegen, 1984).Google Scholar
7.Hadwiger, H.. Vorlesungen über lnhalt, Oberfläche und Isoperimetrie (Springer-Verlag, Berlin, Göttingen, Heidelberg, 1957).CrossRefGoogle Scholar
8.Larman, D. G. and Rogers, C. A.. Paths in the one-skeleton of a convex body. Mathematika. 17 (1970), 293–314.CrossRefGoogle Scholar
9.McMullen, P.. Non-linear angle-sum relations for polyhedral cones and polytopes. Math. Proc. Camb. Phil. Soc., 78 (1975), 247–261.CrossRefGoogle Scholar
10.Rogers, C. A.. Packing and covering (Cambridge University Press, 1964).Google Scholar
11.Wills, J. M.. Research problems 30, 33 and 35. Periodica Math. Hung., (a) 13 (1982), 75 76; (b) 14 (1983), 189–191 and (c) 14 (1983), 312–314.CrossRefGoogle Scholar