Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-04T21:15:36.322Z Has data issue: false hasContentIssue false
  • English
  • Français

THE ROBUSTNESS OF EQUILIBRIA ON CONVEX SOLIDS

Part of: Applications to physics - Differential geometry Classical differential geometry

Published online by Cambridge University Press:  19 December 2013

Gábor Domokos  and
Zsolt Lángi
Gábor Domokos
Affiliation:
Department of Mechanics, Materials and Structures, Budapest University of Technology, Műegyetem rakpart 1-3, 1111 Budapest, Hungary email [email protected]
Zsolt Lángi
Affiliation:
Department of Geometry, Budapest University of Technology, Egry József u. 1, 1111 Budapest, Hungary email [email protected]
Get access

Abstract

We examine the minimal magnitude of perturbations necessary to change the number 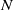$N$ of static equilibrium points of a convex solid 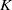$K$. We call the normalized volume of the minimally necessary truncation robustness and we seek shapes with maximal robustness for fixed values of 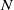$N$. While the upward robustness (referring to the increase of 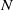$N$) of smooth, homogeneous convex solids is known to be zero, little is known about their downward robustness. The difficulty of the latter problem is related to the coupling (via integrals) between the geometry of the hull 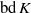$\mathrm{bd} \hspace{0.167em} K$ and the location of the center of gravity 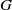$G$. Here we first investigate two simpler, decoupled problems by examining truncations of 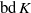$\mathrm{bd} \hspace{0.167em} K$ with $G$ fixed, and displacements of 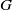$G$ with 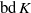$\mathrm{bd} \hspace{0.167em} K$ fixed, leading to the concept of external and internal robustness, respectively. In dimension 2, we find that for any fixed number 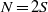$N= 2S$, the convex solids with both maximal external and maximal internal robustness are regular 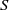$S$-gons. Based on this result we conjecture that regular polygons have maximal downward robustness also in the original, coupled problem. We also show that in the decoupled problems, three-dimensional regular polyhedra have maximal internal robustness, however, only under additional constraints. Finally, we prove results for the full problem in the case of three-dimensional solids. These results appear to explain why monostatic pebbles (with either one stable or one unstable point of equilibrium) are found so rarely in nature.

MSC classification

Secondary: 53A05: Surfaces in Euclidean space 53Z05: Applications to physics
Type
Research Article
Information
Mathematika , Volume 60 , Issue 1 , January 2014 , pp. 237 - 256
Copyright
Copyright © University College London 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arnold, V. I., Ordinary Differential Equations, 10th printing, MIT Press (Cambridge, MA, 1998).Google Scholar
Blaschke, W., Kreis und Kugel, de Gruyer (Berlin, 1956).CrossRefGoogle Scholar
Bloore, F. J., The shape of pebbles. Math. Geol. 9 (1977), 113–122.Google Scholar
Dawson, R., Monostatic simplexes. Amer. Math. Monthly 92 (1985), 541–546.Google Scholar
Dawson, R., Finbow, W. and Mak, P., Monostatic simplexes II. Geom. Dedicata 70 (1998), 209–219.Google Scholar
Dawson, R. and Finbow, W., What shape is a loaded die? Math. Intelligencer 22 (1999), 32–37.CrossRefGoogle Scholar
Do Carmo, M. P., Differential Geometry of Curves and Surfaces, Prentice-Hall (Englewood Cliffs, NJ, 1976).Google Scholar
Domokos, G. and Gibbons, G. W., The evolution of pebble shape in space and time. Proc. Roy. Soc. London (2012), doi:10.1098/rspa.2011.0562.Google Scholar
Domokos, G., Lángi, Z. and Szabó, T., On the equilibria of finely discretized curves and surfaces. Monatsh. Math. (2012), doi:10.1007/s00605-011-0361-x.Google Scholar
Domokos, G., Lángi, Z. and Szabó, T., The genealogy of convex solids. Preprint, 2012, arXiv:1204.5494.Google Scholar
Domokos, G., Ruina, A. and Papadopoulos, J., Static equilibria of rigid bodies: is there anything new? J. Elasticity 36 (1) (1994), 59–66.CrossRefGoogle Scholar
Domokos, G., Sipos, A. Á., Szabó, T. and Várkonyi, P., Pebbles, shapes and equilibria. Math. Geosci. 42 (1) (2010), 29–47.Google Scholar
Domokos, G. and Várkonyi, P., Geometry and self-righting of turtles. Proc. Roy. Soc. London B 275 (1630) (2008), 11–17.Google Scholar
Firey, W. J., The shape of worn stones. Mathematika 21 (1974), 1–11.Google Scholar
Fejes Tóth, L., Regular Figures, Pergamon (Oxford, 1964).Google Scholar
Heath, T. I. (ed.) The Works of Archimedes, Cambridge University Press (Cambridge, 1897).Google Scholar
Heppes, A., A double-tipping tetrahedron. SIAM Rev. 9 (1967), 599–600.Google Scholar
Krapivsky, P. L. and Redner, S., Smoothing a rock by chipping. Phys. Rev. E 9 (2007), 75(3 Pt 1):031119.Google Scholar
Krynine, P. D., On the antiquity of sedimentation and hydrology. Bull. Geol. Soc. Amer. 71 (1960), 1721–1726.Google Scholar
Milnor, J., Morse Theory, Princeton University Press (Princeton, NJ, 1963).CrossRefGoogle Scholar
Poston, T. and Stewart, J., Catastrophe Theory and Its Applications, Pitman (London, 1978).Google Scholar
Rayleigh, Lord, Pebbles, natural and artificial. Their shape under various conditions of abrasion. Proc. R. Soc. Lond. A 181 (1942), 107–118.Google Scholar
Santaló, L. A., Integral Geometry and Geometric Probability, Addison-Wesley (Reading, MA, 1976).Google Scholar
Schrott, M. and Odehnal, B., Ortho-circles of Dupin cyclides. J. Geom. Graph. 10 (2006), 73–98.Google Scholar
Simsek, A., Ozdaglar, A. and Acemoglu, D., Generalized Poincaré–Hopf theorem for compact nonsmooth regions. Math. Oper. Res. 32 (1)193–214.Google Scholar
Tammes, P. M. L., On the origin of number and arrangement of the places of exit on pollen grains. Diss. Groningen (1930).Google Scholar
Várkonyi, P. L. and Domokos, G., Static equilibria of rigid bodies: dice, pebbles and the Poincaré–Hopf theorem. J. Nonlinear Sci. 16 (2006), 255–281.CrossRefGoogle Scholar
Zamfirescu, T., How do convex bodies sit? Mathematica 42 (1995), 179–181.Google Scholar