Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-26T16:30:40.377Z Has data issue: false hasContentIssue false
  • English
  • Français

Reversion of a formal power series

Published online by Cambridge University Press:  26 February 2010

J. A. Tyrrell
J. A. Tyrrell
Affiliation:
King's College, London.
Get access

Extract

If f(z) is a function of the complex variable z, regular in a neighbourhood of z = 0, with f (0) = 0 and f' (0) ≠ 0, then the equation w = f(z) admits a unique solution, regular in some neighbourhood of w = 0, given by

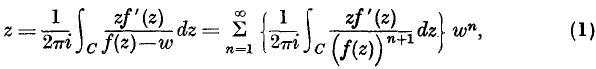
where C is an appropriate contour encircling z = 0. These formulae are well-known, being stages in the proof of the classical reversion † formula

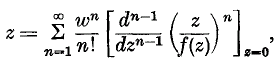
due to Lagrange.

Type
Research Article
Information
Mathematika , Volume 9 , Issue 1 , June 1962 , pp. 88 - 94
Copyright
Copyright © University College London 1962

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

† We use the word “reversion” rather than “inversion”, to avoid any confusion with the algebraic use of “inverse” when “reciprocal” is meant.