Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Needell, Deanna
and
Tropp, Joel A.
2014.
Paved with good intentions: Analysis of a randomized block Kaczmarz method.
Linear Algebra and its Applications,
Vol. 441,
Issue. ,
p.
199.
Kashin, Boris Sergeevich
2015.
О методе Лунина нахождения больших подматриц с малой нормой.
Математический сборник,
Vol. 206,
Issue. 7,
p.
95.
Youssef, Pierre
2015.
Extracting a basis with fixed block inside a matrix.
Linear Algebra and its Applications,
Vol. 469,
Issue. ,
p.
28.
Kashin, B S
2015.
Lunin's method for selecting large submatrices with small norm.
Sbornik: Mathematics,
Vol. 206,
Issue. 7,
p.
980.
Naor, Assaf
and
Youssef, Pierre
2017.
A Journey Through Discrete Mathematics.
p.
657.
Chrétien, Stéphane
and
Ho, Olivier
2018.
Latent Variable Analysis and Signal Separation.
Vol. 10891,
Issue. ,
p.
127.
Tikhomirov, Konstantin
2019.
On the Banach–Mazur distance to cross-polytope.
Advances in Mathematics,
Vol. 345,
Issue. ,
p.
598.
Dilworth, Stephen J.
Kutzarova, Denka
and
Ostrovskii, Mikhail I.
2020.
Lipschitz-free Spaces on Finite Metric Spaces.
Canadian Journal of Mathematics,
Vol. 72,
Issue. 3,
p.
774.
Cabello Sánchez, Javier
and
Morales González, Daniel
2021.
The Banach Space of Quasinorms on a Finite-Dimensional Space.
The Journal of Geometric Analysis,
Vol. 31,
Issue. 11,
p.
11338.
Xie, Jiaxin
and
Xu, Zhiqiang
2021.
Subset selection for matrices with fixed blocks.
Israel Journal of Mathematics,
Vol. 245,
Issue. 1,
p.
1.
Marcus, Adam W.
Spielman, Daniel A.
and
Srivastava, Nikhil
2022.
Interlacing families III: Sharper restricted invertibility estimates.
Israel Journal of Mathematics,
Vol. 247,
Issue. 2,
p.
519.
Nikolov, Aleksandar
Singh, Mohit
and
Tantipongpipat, Uthaipon (Tao)
2022.
Proportional Volume Sampling and Approximation Algorithms for A-Optimal Design.
Mathematics of Operations Research,
Vol. 47,
Issue. 2,
p.
847.
Baudier, Florent
Motakis, Pavlos
Schlumprecht, Thomas
and
Zsák, András
2022.
Stochastic approximation of lamplighter metrics.
Bulletin of the London Mathematical Society,
Vol. 54,
Issue. 5,
p.
1804.
Krishna, K. Mahesh
2022.
Modular Bourgain-Tzafriri Restricted Invertibility Conjectures and Johnson-Lindenstrauss Flattening Conjecture.
SSRN Electronic Journal ,
Zhang, Longzhen
Meng, Lingxu
and
Wu, Senlin
2023.
Banach–Mazur Distance from $$\ell_p^3$$ to $$\ell_\infty^3$$.
Mathematical Notes,
Vol. 114,
Issue. 5-6,
p.
1045.
Cai, Jian-Feng
Xu, Zhiqiang
and
Xu, Zili
2024.
Interlacing Polynomial Method for the Column Subset Selection Problem.
International Mathematics Research Notices,
Vol. 2024,
Issue. 9,
p.
7798.
 $n$-dimensional normed space from
$n$-dimensional normed space from  ${ \ell }_{\infty }^{n} $ is at most
${ \ell }_{\infty }^{n} $ is at most 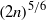 $\mathop{(2n)}\nolimits ^{5/ 6} $. Finally, using tools from the work of Batson et al in [Twice-Ramanujan sparsifiers. In STOC’09 – Proceedings of the 2009 ACM International Symposium on Theory of Computing, ACM (New York, 2009), 255–262], we give a new proof for a theorem of Kashin and Tzafriri [Some remarks on the restriction of operators to coordinate subspaces. Preprint, 1993] on the norm of restricted matrices.
$\mathop{(2n)}\nolimits ^{5/ 6} $. Finally, using tools from the work of Batson et al in [Twice-Ramanujan sparsifiers. In STOC’09 – Proceedings of the 2009 ACM International Symposium on Theory of Computing, ACM (New York, 2009), 255–262], we give a new proof for a theorem of Kashin and Tzafriri [Some remarks on the restriction of operators to coordinate subspaces. Preprint, 1993] on the norm of restricted matrices.