Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-24T16:30:54.008Z Has data issue: false hasContentIssue false
  • English
  • Français

The representation of integers by positive ternary quadratic forms

Published online by Cambridge University Press:  26 February 2010

G. L. Watson
G. L. Watson
Affiliation:
University College, London
Get access

Extract

Let f = f(x, y, z) be a positive definite form of the type

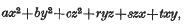
where x, y, z are integral valued variables, and the coefficients a, …, t are integers whose highest common factor is 1. As the determinant of such a form may be fractional, I define

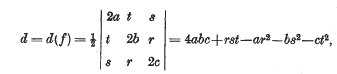
and

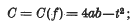
thus — C is the discriminant of the binary form f(x, y, 0), and the necessary and sufficient condition for f to be positive definite is that a > 0, C > 0, and d > 0.

Type
Research Article
Information
Mathematika , Volume 1 , Issue 2 , June 1954 , pp. 104 - 110
Copyright
Copyright © University College London 1954

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

page note 104 * Izvestia Akad. Nauk S.S.S.R. 4, (1940) 363–402.Google Scholar

page note 104 † Annals of Math., 28 (1927), 333–341.Google Scholar

page note 104 ‡ Acta Math., 70 (1939), 165–191.CrossRefGoogle Scholar

page note 106 * See e.g., Hardy, G. H. and Wright, E. M., An Introduction to the Theory of Numbers Oxford, 1938), 96, Theorem 123.Google Scholar

page note 107 * Nachrichten K. Ges. Wiss. Göttingen, Math.-Phya. Klasse, 1918, 21–29. Pólya states the result for a proper character, but this restriction is easily removed.