No CrossRef data available.
Published online by Cambridge University Press: 26 February 2010
For arbitrary f: R → R and ϒ ⊂ Z × R we define the set 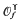 of quantized observations of f relative to ϒ as follows: for each integer n and each y∈R we write
of quantized observations of f relative to ϒ as follows: for each integer n and each y∈R we write
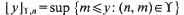
(the supremum of an empty set is taken to be −∞ ) and we put
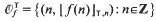
Thus for example 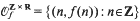 and
and 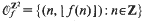 , where [x] (without subscript) denotes as usual the integer part of x.
, where [x] (without subscript) denotes as usual the integer part of x.