For a metric space <Ω, ρ> and a ‘measure function’ h, the Hausdorff measure mh on Ω is denned by applying Method II to the premeasure defined by τ(E) = h(d(E)), E ⊆ Ω, where

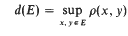
with d(Φ) = 0, is the diameter of E. The set function mh is then a metric outer measure. There are many variations on this definition producing measures also associated with the name Hausdorff. Here we are concerned with those measures which arise when there is a restriction on the sets E for which τ is defined. Such measures arise, for example, as net measures, Rogers [1]. Also we might find it useful to have τ defined only on disks, or only on squares, or only on rectangles with a given relation between vertical and horizontal sides.