Hostname: page-component-5cf477f64f-2wr7h Total loading time: 0 Render date: 2025-04-06T14:28:28.600Z Has data issue: false hasContentIssue false
  • English
  • Français

A RANGE PROPERTY RELATED TO NON-EXPANSIVE OPERATORS

Part of: Existence theories Nonlinear operators and their properties

Published online by Cambridge University Press:  06 August 2013

Biagio Ricceri
Biagio Ricceri*
Affiliation:
Department of Mathematics, University of Catania, Viale A. Doria 6, 95125 Catania, Italy email [email protected]
Get access

Abstract

In this paper, we prove that if 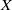$X$ is an infinite-dimensional real Hilbert space and 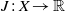$J: X\rightarrow \mathbb{R} $ is a sequentially weakly lower semicontinuous 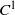${C}^{1} $ functional whose Gâteaux derivative is non-expansive, then there exists a closed ball 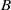$B$ in 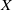$X$ such that 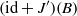$(\mathrm{id} + {J}^{\prime } )(B)$ intersects every convex and dense subset of 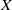$X$.

MSC classification

Secondary: 47H09: Contraction-type mappings, nonexpansive mappings, $A$-proper mappings, etc. 47H05: Monotone operators and generalizations 49J35: Minimax problems
Type
Research Article
Information
Mathematika , Volume 60 , Issue 1 , January 2014 , pp. 232 - 236
Copyright
Copyright © University College London 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Goebel, K. and Reich, S., Uniform Convexity, Hyperbolic Geometry, and Nonexpansive Mappings, Marcel Dekker (New York, 1984).Google Scholar
Minty, G. J., Monotone (nonlinear) operators in Hilbert space. Duke Math. J. 29 (1962), 341–346.Google Scholar
Moreau, J.-J., Proximité et dualité dans un espace hilbertien. Bull. Soc. Math. France 93 (1965), 273–299.Google Scholar
Ricceri, B., The problem of minimizing locally a ${C}^{2} $ functional around non-critical points is well-posed. Proc. Amer. Math. Soc. 135 (2007), 2187–2191.CrossRefGoogle Scholar
Ricceri, B., A strict minimax inequality criterion and some of its consequences. Positivity 16 (2012), 455–470.Google Scholar
Zeidler, E., Nonlinear Functional Analysis and its Applications, Vol. III, Springer (New York, 1985).CrossRefGoogle Scholar