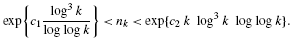No CrossRef data available.
Published online by Cambridge University Press: 21 December 2009
For each integer n ≥ 2, let β(n) stand for the product of the exponents in the prime factorization of n. Given an arbitrary integer k ≥ 2, let nk be the smallest positive integer n such that β(n + 1) = β(n + 2) = … = β(n + k). We prove that there exist positive constants c1 and c2 such that, for all integers k ≥ 2,