Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-23T15:17:18.855Z Has data issue: false hasContentIssue false
  • English
  • Français

Primitive polynomial subsequences

Published online by Cambridge University Press:  26 February 2010

I. Anderson ,
S. D. Cohen  and
W. W. Stothers
I. Anderson
Affiliation:
Department of Mathematics, University of Glasgow, Glasgow G12 8QW
S. D. Cohen
Affiliation:
Department of Mathematics, University of Glasgow, Glasgow G12 8QW
W. W. Stothers
Affiliation:
Department of Mathematics, University of Glasgow, Glasgow G12 8QW
Get access

Extract

A sequence {an} of integers is said to be primitive if 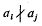whenever i ≠ j. For example, if n is any positive integer, the sequence

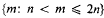
is primitive. This is an important example in the light of the elementary result (see [2; p. 244]) that if 0 < a1 < a2 < … < ar ≤ 2n is primitive then necessarily r ≤ n; i.e. at most half of the positive integers ≤ 2n can be members of the sequence. Besicovitch [2; p. 257] has obtained the surprising result that, given ε > 0, there exists an infinite primitive sequence {ai} such that

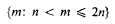
where A(n) denotes the number of ai ≤ n.

Type
Research Article
Information
Mathematika , Volume 21 , Issue 2 , December 1974 , pp. 239 - 247
Copyright
Copyright © University College London 1974

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Davenport, H. and Roth, K. F.. “Rational approximations to algebraic numbers”, Mathematika, 2 (1955), 160–167.CrossRefGoogle Scholar
2.Halberstam, H. and Roth, K. F.. Sequences, Vol. 1 (Oxford 1966).Google Scholar
3.Leveque, W. J.. Topics in Number Theory, Vol. 1 (Addison-Wesley 1956).Google Scholar
4.Odoni, R. W. K.. “The Farey density of norm subgroups of global fields (1)”, Mathematika, 20 (1973), 155–169.CrossRefGoogle Scholar
5.Smith, H. J. S.. “Reports on the Theory of Numbers”, Collected Mathematical Papers, Vol. 1 (Oxford 1894).Google Scholar