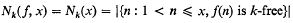Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Erdös, P.
1981.
Analytic Number Theory.
Vol. 899,
Issue. ,
p.
171.
Filaseta, Michael
1988.
An elementary approach to short interval results for k-free numbers.
Journal of Number Theory,
Vol. 30,
Issue. 2,
p.
208.
Ichimura, Humio
1996.
A note on the lwasawa $\lambda$-invariants of real quadratic fields.
Proceedings of the Japan Academy, Series A, Mathematical Sciences,
Vol. 72,
Issue. 1,
Schinzel, A.
1997.
The Mathematics of Paul Erdös I.
Vol. 13,
Issue. ,
p.
151.
Lee, Jung-Jo
and
Murty, M. Ram
2007.
Dirichlet series and hyperelliptic curves.
Forum Mathematicum,
Vol. 19,
Issue. 4,
Browning, T. D.
2011.
Power-free values of polynomials.
Archiv der Mathematik,
Vol. 96,
Issue. 2,
p.
139.
Narkiewicz, Władysław
2012.
Rational Number Theory in the 20th Century.
p.
131.
Schinzel, Andrzej
2013.
The Mathematics of Paul Erdős I.
p.
263.
GROSS, SAMUEL S.
and
VINCENT, ANDREW F.
2013.
ON THE FACTORIZATION OF f(n) FOR f(x) IN ℤ[x].
International Journal of Number Theory,
Vol. 09,
Issue. 05,
p.
1225.
Cho, Peter J.
and
Kim, Henry H.
2013.
Logarithmic derivatives of Artin -functions.
Compositio Mathematica,
Vol. 149,
Issue. 4,
p.
568.
Rudnick, Zeév
2014.
Square-free values of polynomials over the rational function field.
Journal of Number Theory,
Vol. 135,
Issue. ,
p.
60.
Lando, Guy
2015.
SQUARE-FREE VALUES OF POLYNOMIALS EVALUATED AT PRIMES OVER A FUNCTION FIELD.
The Quarterly Journal of Mathematics,
Vol. 66,
Issue. 3,
p.
905.
Filaseta, M.
Graham, S.
and
Trifonov, O.
2015.
Starting with gaps between k-free numbers.
International Journal of Number Theory,
Vol. 11,
Issue. 05,
p.
1411.
Reuss, T.
2015.
Power‐free values of polynomials.
Bulletin of the London Mathematical Society,
Vol. 47,
Issue. 2,
p.
270.
Xiao, Stanley Yao
2016.
Power-Free Values of Binary Forms and the Global Determinant Method.
International Mathematics Research Notices,
p.
rnw165.
Kim, Henry H.
and
Wolske, Zack
2018.
Number fields with large minimal index containing quadratic subfields.
International Journal of Number Theory,
Vol. 14,
Issue. 09,
p.
2333.
Kim, Henry H.
2019.
Monogenic dihedral quartic extensions.
The Ramanujan Journal,
Vol. 50,
Issue. 2,
p.
459.
Umegaki, Atsuki
and
Umegaki, Yumiko
2020.
Quartic fields with large class numbers.
Rocky Mountain Journal of Mathematics,
Vol. 50,
Issue. 1,
Dimitrov, Stoyan Ivanov
2023.
Square-free values of n
2 + n + 1.
Georgian Mathematical Journal,
Vol. 30,
Issue. 3,
p.
333.