Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-23T19:09:25.297Z Has data issue: false hasContentIssue false
  • English
  • Français

Piatetski-Shapiro prime k-tuplets

Part of: Multiplicative number theory

Published online by Cambridge University Press:  26 February 2010

Glyn Harman
Glyn Harman
Affiliation:
School of Mathematics, Cardiff University of Wales, P.O. Box 926, Cardiff CF2 4YH.
Get access

Extract

The question as to which “natural” sequences contain infinitely many primes is of considerable fascination to the number-theorist. One such “natura” sequence is [nc[ where [·] denotes integer part. Piatetski-Shapiro [10] showed that there are infinitely many primes in this sequence for 1 < c < 12/11, obtaining the expected asymptotic formula for the number of such primes. The exponent 12/11 has been increased gradually by a number of authors to the present record 45/38 held by Kumchev [9]. It is expected that there are infinitely many primes of the form [nc[ for all cεε[1, ∞)/ℤ. Deshouillers [3] showed that this is almost always true, in the sense of Lebesgue measure on [1, ∞). Balog [2] improved and generalized this result to show that, for almost all c > 1,

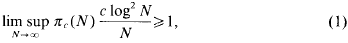
where

MSC classification

Secondary: 11N05: Distribution of primes
Type
Research Article
Information
Mathematika , Volume 45 , Issue 2 , December 1998 , pp. 351 - 357
Copyright
Copyright © University College London 1998

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Baker, R. C. and Harman, G.. Primes of the form [cP]. Math. Zeit., 221 (1996), 7381.CrossRefGoogle Scholar
2.Balog, A.. On a variant of the Piatetski- Shapiro Prime Number Theorem. Groupe de Travail en Théorie Analytique et Elementaire des Nombres 1987-1988, 3–11 (Université de Paris XI, Orsay, 1989).Google Scholar
3.DeshouilersJ,-M. J,-M.. Nombres premiers de la forme [n c]. C. R. Acad. Sci. Paris Ser. A-B, 282 (1976), A131–133.Google Scholar
4.Graham, S. W. and Kolesnik, G.. Van der Corput's Method of Exponential Sums, London Math. Soc. Lecture Note Series, 126 (Cambridge University Press, 1991).Google Scholar
5.Halberstam, H. and Richert, H.-R.. Sieve Methods (Academic Press, New York/London, 1974).Google Scholar
6.Harman, G.. Metric Diophantine Approximation with two restricted variables III: Two prime numbers. J. Number Theory, 29 (1988), 364375.Google Scholar
7.Harman, G.. Metrical theorems on prime values of the integer parts of real sequences. Proc. London Math. Soc. (3), 75 (1997), 481–496.CrossRefGoogle Scholar
8.Heath-Brown, D. R.. The differences between consecutive primes. J. London Math. Soc. (2), 18 (1978), 713.Google Scholar
9.Kumchev, A.. On the distribution of prime numbers of the form [n2. Glasgow Math. J. To appear.Google Scholar
10.Piatetski-Shapiro, I.. On the distribution of prime numbers of the form [f(n)]. Math. Sb., 33 (1953), 559–566.Google Scholar
11.Sullivan, D.. Disjoint spheres, approximation by imaginary quadratic numbers, and logarithmic law for geodesies. Acta Math., 149 (1983), 215237.Google Scholar