Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-26T17:41:20.534Z Has data issue: false hasContentIssue false
  • English
  • Français

Ovaloids whose curvatures are powers of support functions

Part of: Global differential geometry

Published online by Cambridge University Press:  26 February 2010

Chr. Georgiou  and
Th. Hasanis
Chr. Georgiou
Affiliation:
Department of Mathematics, University of Ioannina, Ioannina, Greece.
Th. Hasanis
Affiliation:
Department of Mathematics, University of Ioannina, Ioannina, Greece.
Get access

Extract

Let Mn be a smooth, compact and strictly convex, embedded hypersurface of Rn + 1 (n ≥ 1), an ovaloid for short. By “strictly convex” we mean that the Gauss-Kronecker curvature 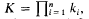where ki are the principal curvatures with respect to the inner unit normal field, is everywhere positive. It is well knpwn [5, p. 41] that, for such a hypersurface, the spherical-image mapping is a diffeomorphism onto the unit hypersphere. Furthermore, Mn is the boundary of an open bounded convex body, which we shall call the interior of Mn.

MSC classification

Secondary: 53C45: Global surface theory (convex surfaces à la A. D. Aleksandrov)
Type
Research Article
Information
Mathematika , Volume 28 , Issue 2 , December 1981 , pp. 192 - 197
Copyright
Copyright © University College London 1981

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Blaschke, W.. Vortesungen über Integralgeometrie (Chelsea Publishing Company, New York, 1949).Google Scholar
2.Cheng, S.-Y. and Yau, S.-T.. “On the regularity of the solution of the n-dimensional Minkowski problem”, Comm. Pure Appl. Math., 29 (1976), 495–516.CrossRefGoogle Scholar
3.Chern, S. S.. “Integral formulas for hypersurfaces in Euclidean spaces and their applications to uniqueness theorems”, J. Math. Mech., 8 (1959), 947–956.Google Scholar
4.Flanders, H.. “The Steiner point of a closed hypersurface”, Mathematika, 13 (1966), 181–188.CrossRefGoogle Scholar
5.Kobayashi, S. and Nomizu, K.. Foundations of Differential Geometry, Vol. II (Interscience Publishers, New York, 1969).Google Scholar
6.Koutroufiotis, D.. “Ovaloids which are almost spheres”, Comm. Pure Appl. Math., XXIV (1971), 289–300.CrossRefGoogle Scholar
7.Pogorelov, A.. “On a regular solution of the n-dimensional Minkowski problem”, Sov. Math. Dokl, 12 (1971), 1192–1196.Google Scholar
8.Struik, D.. Lectures on classical Differential Geometry (Addison-Wesley, London, 1961).Google Scholar